Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 11
Activité 3 - Activité d'exploration
Référentiel et vitesse
13 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif : Citer et exploiter les expressions des coordonnées des vecteurs vitesse et accélération dans le repère de Frenet pour un mouvement circulaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problématique de l'activité
Le mensuel Science & Vie répond chaque mois aux questions des lecteurs. La
notion de relativité du mouvement est ici interrogée.
La vitesse d'un système dépend-elle du référentiel d'étude ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Rotation de la Terre
Si vous prenez pour référence [l'axe de rotation de la Terre], vous atteignez 1 100 km·h-1 à la latitude de Marseille, puisque votre parallèle mesure 26 800 km que vous parcourez en 24 h, à l'équateur, vous iriez à 1 670 km·h‑1.
Le vertige commence quand on songe que votre fauteuil tourne autour du Soleil sur une orbite de 940 millions de kilomètres qu'il parcourt en 1 an et 6 heures, soit 107 000 km·h-1. Et le Soleil lui-même tourne autour du centre de la galaxie, accomplissant une révolution galactique à 965 000 km·h-1.
Le vertige commence quand on songe que votre fauteuil tourne autour du Soleil sur une orbite de 940 millions de kilomètres qu'il parcourt en 1 an et 6 heures, soit 107 000 km·h-1. Et le Soleil lui-même tourne autour du centre de la galaxie, accomplissant une révolution galactique à 965 000 km·h-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Point à la surface de la Terre
Le zoom est accessible dans la version Premium.
Un point à la surface de la Terre peut être repéré par deux grandeurs :
- la longitude \beta, angle de positionnement est-ouest d'un point sur Terre par rapport au méridien de Greenwich ;
- la latitude \lambda, angle de positionnement nord-sud d'un point sur Terre par rapport à l'équateur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Repère de Frenet
Le zoom est accessible dans la version Premium.
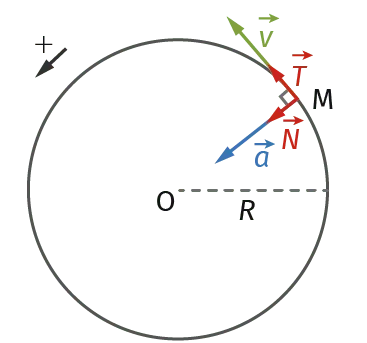
Pour les mouvements circulaires, on définit un repère, dit de Frenet. Celui-ci est constitué de deux vecteurs unitaires : \overrightarrow{T} qui est tangent à la trajectoire au point M et \overrightarrow{N} qui est un vecteur centripète.
Pour les mouvements circulaires uniformes, de vitesse v, on peut exprimer \vec{a} :
\vec{a} = \dfrac{v^2}{R} \cdot \overrightarrow{N}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
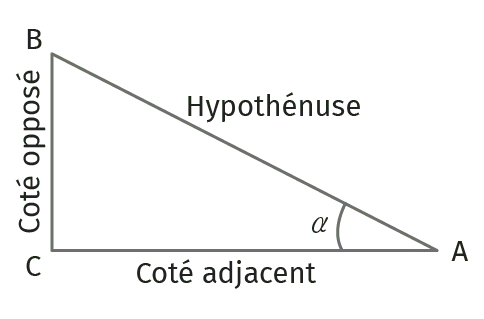
Dans un triangle rectangle :
\cos(\alpha) = \dfrac{\text{AC}}{\text{AB}}
\sin(\alpha) = \dfrac{\text{BC}}{\text{AB}}
\cos(\alpha) = \dfrac{\text{AC}}{\text{AB}}
\sin(\alpha) = \dfrac{\text{BC}}{\text{AB}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Rayon de la Terre : R_\text{T} = 6\ 370 km
- Distance entre la Terre et le Soleil : d = 1{,}5 \times 10^{11} m
- Expression du périmètre p d'un cercle de rayon r : p = 2\ \pi \cdot r
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Découvrez à quelle vitesse se déplace la Terre dans l'espace en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Compétence(s)
APP : Extraire l'information utile
VAL : Évaluer et connaître des ordres de grandeur
VAL : Évaluer et connaître des ordres de grandeur
1. Relever, pour chaque référentiel cité dans le , la vitesse de déplacement qui lui est associée.
2. Déterminer la distance à l'axe de rotation de la ville de Marseille, c'est-à-dire la distance entre Marseille et sa projection sur l'axe de rotation au point \text{O} (), puis sa latitude \lambda.
3. Calculer la valeur de l'accélération à l'équateur due à la rotation de la Terre et la comparer à l'accélération due à la pesanteur notée g = 9{,}81 m·s-2. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Synthèse de l'activité
En reprenant le même raisonnement, déterminer l'accélération due à la révolution de la Terre autour du Soleil. La comparer avec la valeur précédemment calculée.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah