Physique-Chimie Terminale Spécialité

Rejoignez la communauté !

Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.

Préparation aux épreuves du Bac

1. Constitution et transformations de la matière

Composition et évolution d'un système

Ouverture de thème p. 16-17

Ch. 1

Modélisation des transformations acide-base

Ch. 2

Analyse physique d'un système chimique

Ch. 3

Méthode de suivi d'un titrage

Ch. 4

Évolution temporelle d'une transformation chimique

Ch. 5

Évolution temporelle d'une transformation nucléaire

BAC

Thème 1

Prévision et stratégie en chimie

Ouverture de thème p. 146-147

Ch. 6

Évolution spontanée d'un système chimique

Ch. 7

Équilibres acide-base

Ch. 8

Transformations chimiques forcées

Ch. 9

Structure et optimisation en chimie organique

Ch. 10

Stratégies de synthèse

BAC

Thème 1 bis

2. Mouvement et interactions

Ouverture de thème

p. 290-291

Ch. 11

Description d'un mouvement

Ch. 12

Mouvement dans un champ uniforme

Ch. 13

Mouvement dans un champ de gravitation

Ch. 14

Modélisation de l'écoulement d'un fluide

BAC

Thème 2

3. Conversions et transferts d'énergie

Ouverture de thème

p. 402-403

Ch. 15

Étude d’un système thermodynamique

Ch. 16

Bilans d'énergie thermique

BAC

Thème 3

4. Ondes et signaux

Ouverture de thème

p. 462-463

Ch. 17

Propagation des ondes

Ch. 18

Interférences et diffraction

Ch. 19

Lunette astronomique

Ch. 20

Effet photoélectrique et enjeux énergétiques

Ch. 21

Évolutions temporelles dans un circuit capacitif

BAC

Thème 4

Annexes

Ch. 22

Méthode

Chapitre 11

Activité 2 - Activité expérimentale

90 min

Mobile et plan incliné

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Objectif : Déterminer expérimentalement et représenter les coordonnées des vecteurs position, vitesse et accélération en fonction du temps.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Problématique de l'activité

Le skateboard est une discipline exigeante qui nécessite un bon équilibre et une certaine adresse. Les figures réalisées par certains skateurs suivent des trajectoires parfois complexes.

Quels renseignements sur la trajectoire peut-on tirer de la représentation des vecteurs

v

a

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 1
Situation et modélisation expérimentale

Le zoom est accessible dans la version Premium.

Crédits : cassiede alain/Shutterstock

Le zoom est accessible dans la version Premium.

Crédits : lelivrescolaire.fr

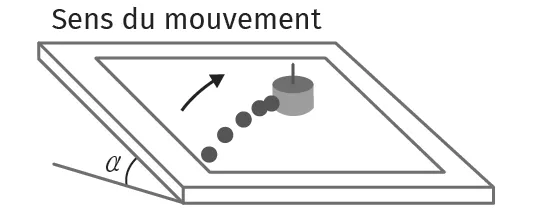
On se propose d'étudier le mouvement d'un skateur s'élançant sur la rampe d'un half-pipe. Pour cela, on modélise le phénomène à l'aide d'une table à coussin d'air inclinée d'un angle

α

.
En considérant un plan incliné, l'accélération subie par le skateur vers le bas de la pente correspond à :

a = g \cdot sin (α)

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 2
Trajectoire du mobile

Le zoom est accessible dans la version Premium.

Crédits : lelivrescolaire.fr

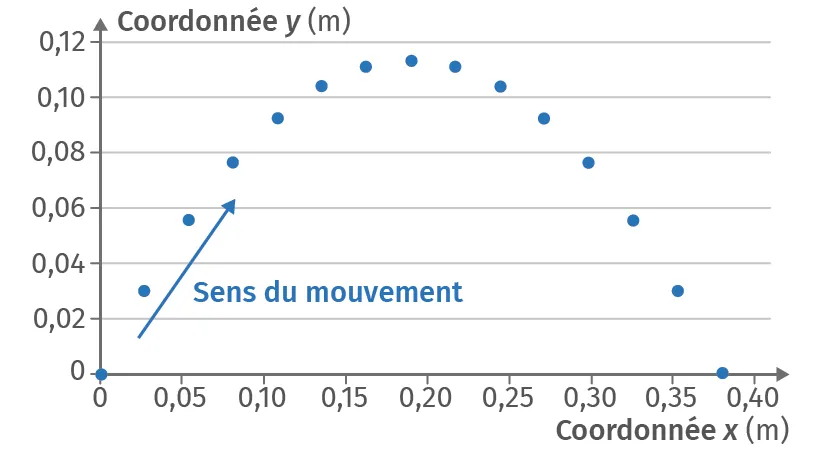
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 3
Approximation du vecteur accélération

Le vecteur accélération

a_{i}

d'un système au point

M_{i}

entre deux dates

t_{i - 1}

t_{i + 1}

a pour expression :

a = \frac{v _{i + 1} - v _{i - 1}}{t _{i + 1} - t _{i - 1}}

Les vecteurs

v_{i - 1}

v_{i + 1}

étant tracés, on peut :

1) tracer le vecteur

Δ v_{i} = v_{i + 1} - v_{i - 1}

;

2) mesurer à la règle la longueur de

Δ v_{i}

et en déduire la valeur en (m·s^-1) du vecteur variation de vitesse grâce à l'échelle des vitesses ;

3) calculer la valeur du vecteur accélération :

a_{i} = \frac{Δ v _{i}}{t _{i + 1} - t _{i - 1}}

;

4) tracer

Δ a_{i}

grâce à l'échelle des accélérations.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Données

Échelle des distances : $1, 0$ cm ↔ $1, 0$ cm
Échelle des vitesses : $1, 0$ cm ↔ $0, 10$ m·s^-1
Échelle des accélérations : $1, 0$ cm ↔ $0, 50$ m·s^-2
Durée entre deux points consécutifs : $τ = 40, 0$ ms
Accélération de pesanteur : $g = 9, 81$ m·s^-2

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Supplément numérique

Téléchargez la
trajectoire
https://assets.lls.fr/pages/15553152/pct11inf8-v3.png
et les
positions
https://assets.lls.fr/pages/15553152/pct11inf7-v2.png
de chaque point du mobile autoporteur.
Téléchargés le
relevé de la modélisation
https://assets.lls.fr/pages/15553152/pct-ch11-releve-modelisation.xlsx
du mouvement.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

VAL : Exploiter un ensemble de mesures
VAL : Analyser des résultats

Compétence(s)

1. Tracer les vecteurs

v

a

d'un point de la trajectoire lors de la phase ascendante et de la phase descendante. Préciser les caractéristiques de ces vecteurs. ➜ Fiche méthode

1, p. 590

2. Déterminer la valeur

a

de l'accélération en effectuant une moyenne des deux mesures.

3. En déduire l'angle d'inclinaison

α

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Synthèse de l'activité

Expliquer pourquoi

a

est constant au cours du mouvement.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Mobile et plan incliné