Physique-Chimie Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 11
Exercices
Pour s'entraîner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20À vélo
✔ RAI/ANA : Construire un raisonnement


Une valve de vélo, située à 55 cm du centre de la roue, tourne à une vitesse de 200 tr·min-1. La vitesse de déplacement du vélo est supposée constante.
1. Déterminer la vitesse de la valve en (m·s-1) dans le référentiel lié au cadre du vélo.
2. En déduire son accélération en (m·s-2).
1. Déterminer la vitesse de la valve en (m·s-1) dans le référentiel lié au cadre du vélo.
2. En déduire son accélération en (m·s-2).
Données
- Expression du périmètre p d'un cercle de rayon r : p = 2 \ \pi \cdot r
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21Mouvement circulaire uniforme
✔ APP : Maîtriser le vocabulaire du cours
Une voiture roule à une vitesse constante de 72 km·h-1 sur une piste circulaire de 100 m de rayon.
1. Déterminer l'accélération de la voiture.
1. Déterminer l'accélération de la voiture.
2. Réaliser un schéma sur lequel on représentera pour un point \text{M} quelconque :
- sa position à l'échelle 1,0 cm ↔ 50 m ;
- son vecteur vitesse à l'échelle 1,0 cm ↔ 10 m·s‑1 ;
- son vecteur accélération à l'échelle 1,0 cm ↔ 2,0 m·s‑2.
Cliquez pour accéder à une zone de dessin
3. Déterminer la période T du mouvement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22Position d'arrêt
✔ APP : Maîtriser le vocabulaire du cours
Le mouvement d'un mobile se déplaçant en ligne droite est représenté ci-dessous.

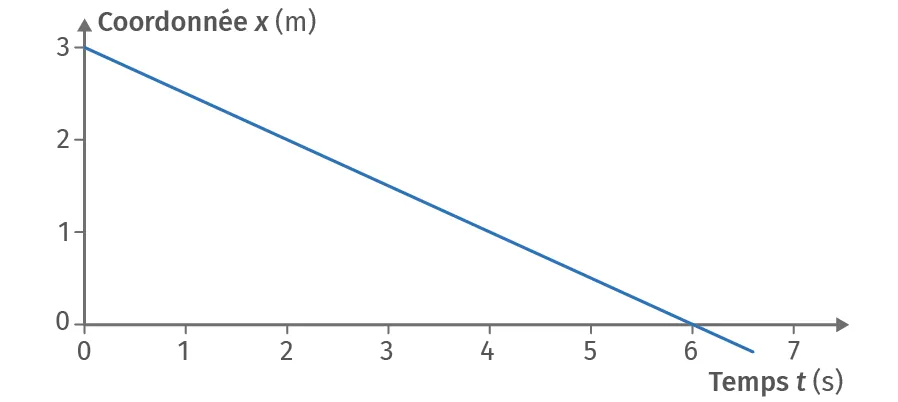


1. Déterminer l'équation horaire x(t).
2. Déterminer l'équation horaire v_x(t).
3. Qualifier le mouvement du mobile à l'aide du vocabulaire adéquat.
4. Déterminer la position du mobile au bout de 10,0 s.
2. Déterminer l'équation horaire v_x(t).
3. Qualifier le mouvement du mobile à l'aide du vocabulaire adéquat.
4. Déterminer la position du mobile au bout de 10,0 s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23Saut à l'élastique
✔ RAI/ANA : Construire un raisonnement
Le mouvement d'un sauteur à l'élastique équipé de son harnais de sécurité est étudié dans le référentiel terrestre. L'évolution de l'altitude z(t) en fonction du temps est représentée ci-dessous.

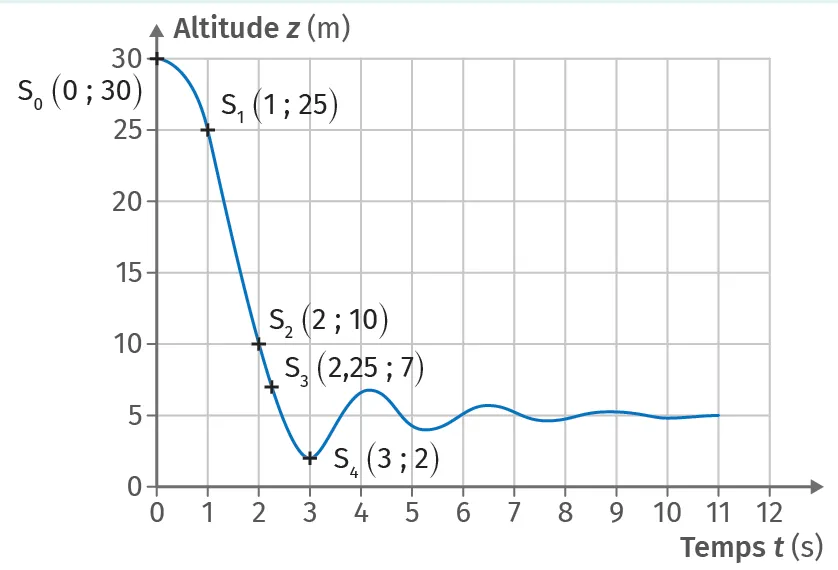
1. Par lecture graphique, déterminer :


1. Par lecture graphique, déterminer :
- la hauteur du pont z_0 ;
- la hauteur de chute minimale hmin ;
- la hauteur finale atteinte hf.
2. En s'appuyant sur le graphique, expliquer la méthode pour déterminer la vitesse verticale initiale de chute notée v_0. Déterminer v_0.
3. L'accélération a(t) est constante lors de la première phase et sa composante vaut a = -10 m·s-2. Montrer que la vitesse v(t) peut alors se mettre sous la forme :
4. Montrer que l'équation horaire z(t) prend la forme :
5. Déterminer la nature de cette première phase du mouvement. En déduire les points parmi S0, S1, S2, S3 et S4 appartenant à cette première phase.
3. L'accélération a(t) est constante lors de la première phase et sa composante vaut a = -10 m·s-2. Montrer que la vitesse v(t) peut alors se mettre sous la forme :
v(t) = a \cdot t + v_0
4. Montrer que l'équation horaire z(t) prend la forme :
z(t) = \dfrac{a}{2} \cdot t^2 + v_0 \cdot t + z_0
5. Déterminer la nature de cette première phase du mouvement. En déduire les points parmi S0, S1, S2, S3 et S4 appartenant à cette première phase.
Détails du barème TOTAL / 5 pts
0,5 pt
1. Lire les valeurs sur un graphique.1 pt
2. Déterminer graphiquement la vitesse v_0.1,5 pt
3. Déterminer v(t) à partir de a.1 pt
4. Déterminer z(t).0,5 pt
4. Vérifier l'expression de z(t).0,5 pt
5. Caractériser un mouvement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Course poursuite en QCM
✔ REA/MATH : Intégrer


Une voiture roule en ligne droite sur l'autoroute à la vitesse constante v_1 = 144 km·h-1, alors que la vitesse est limitée à v_\text{limite} = 130 km·h-1.
Une voiture de gendarmerie démarre au moment où la voiture en excès de vitesse la dépasse, avec une accélération constante telle qu'elle atteint v_2 = 180 km·h-1 en 15,0 s. Une fois à 180 km·h-1, le gendarme maintient cette vitesse jusqu'à rattraper la voiture en excès de vitesse.
On choisit comme origine de l'axe (\text{O}_x) la position de la voiture de gendarmerie à l'arrêt.
Une voiture de gendarmerie démarre au moment où la voiture en excès de vitesse la dépasse, avec une accélération constante telle qu'elle atteint v_2 = 180 km·h-1 en 15,0 s. Une fois à 180 km·h-1, le gendarme maintient cette vitesse jusqu'à rattraper la voiture en excès de vitesse.
On choisit comme origine de l'axe (\text{O}_x) la position de la voiture de gendarmerie à l'arrêt.
1. L'équation horaire de la voiture en excès de vitesse correspond à :
2. La vitesse initiale de la voiture de gendarmerie est :
3. L'accélération de la voiture de la gendarmerie est égale à :
4. Pendant la phase d'accélération, l'équation horaire de la voiture de gendarmerie correspond à :
2. La vitesse initiale de la voiture de gendarmerie est :
3. L'accélération de la voiture de la gendarmerie est égale à :
4. Pendant la phase d'accélération, l'équation horaire de la voiture de gendarmerie correspond à :
5. Au bout de 15,0 s de poursuite, la voiture en excès de vitesse est :
6. Entre le moment où la voiture de gendarmerie démarre et celui où elle arrive au niveau du contrevenant, il s'est écoulé :
7. Au moment où la voiture en excès de vitesse est rattrapée, les deux voitures ont parcouru :
6. Entre le moment où la voiture de gendarmerie démarre et celui où elle arrive au niveau du contrevenant, il s'est écoulé :
7. Au moment où la voiture en excès de vitesse est rattrapée, les deux voitures ont parcouru :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Copie d'élève à commenter
✔ VAL : Faire preuve d'esprit critique
Proposer une justification pour chaque erreur relevée par le correcteur.
Un objet, assimilé à un point matériel noté M, est suivi par l'intermédiaire de ses coordonnées cartésiennes et d'un repère orthonormé (\text{O}\:,\vec{i}\:,\vec{j}) selon les équations horaires :
\overrightarrow{\text{OM}} \; \bigg(\begin{array}{l} x(t) = - \dfrac{a}{2} \cdot t^2 + v_{0x} \cdot t \\ y(t) = v_{0y} \cdot t + h \end{array}\bigg)_{(\text{O},\ \overrightarrow{i}, \ \overrightarrow{j})}
avec a = 10{,}0 m·s-2, v_{0x} = 8{,}0 m·s-1, v_{0y} = 5{,}0 m·s-1 et h = -2{,}0 m.
1. Préciser la position initiale du point M.
À t_0 = 0 s, x(t_0) = 0 m et \color{red}\cancel{\color{black}{y(t_0) = 0}} m.
2. Établir les coordonnées du vecteur vitesse.
Il faut dériver x(t) et y(t) par rapport au temps pour trouver les coordonnées du vecteur vitesse :
v_x(t) = \dfrac{\text{d}x}{\text{d}t}
\color{red}\cancel{\color{black}{v_x(t) = - \dfrac{a}{2} \cdot t + v_{0x}}}
v_y(t) = \dfrac{\text{d}y}{\text{d}t}
\color{red}\cancel{\color{black}{v_y(t) = h}}
v_x(t) = \dfrac{\text{d}x}{\text{d}t}
\color{red}\cancel{\color{black}{v_x(t) = - \dfrac{a}{2} \cdot t + v_{0x}}}
v_y(t) = \dfrac{\text{d}y}{\text{d}t}
\color{red}\cancel{\color{black}{v_y(t) = h}}
3. Déterminer la valeur initiale de la vitesse.
La vitesse initiale s'obtient en exprimant les coordonnées du vecteur vitesse en t_0 = 0 s :
v_x(t_0) = 0 + v_{0x}
AN : v_x(t_0) = 8{,}0 m·s-1
\color{red}\cancel{\color{black}{v_y(t_0) = h}}
AN : \color{red}\cancel{\color{black}{v_y(t_0) = 2{,}0}} m·s-1
\color{red}\cancel{\color{black}{v_0 = v_x(t_0) + v_y(t_0)}}
AN : \color{red}\cancel{\color{black}{v_0 = 8{,}0 + 2{,}0 = 10{,}0}} m·s-1
v_x(t_0) = 0 + v_{0x}
AN : v_x(t_0) = 8{,}0 m·s-1
\color{red}\cancel{\color{black}{v_y(t_0) = h}}
AN : \color{red}\cancel{\color{black}{v_y(t_0) = 2{,}0}} m·s-1
\color{red}\cancel{\color{black}{v_0 = v_x(t_0) + v_y(t_0)}}
AN : \color{red}\cancel{\color{black}{v_0 = 8{,}0 + 2{,}0 = 10{,}0}} m·s-1
4. Établir les coordonnées du vecteur accélération.
L'accélération s'obtient en dérivant la vitesse :
a_x = \dfrac{\text{d}v_x(t)}{\text{d}t}
\color{red}\cancel{\color{black}{a_x(t) = - \dfrac{a}{2}}}
a_y = \dfrac{\text{d}v_y(t)}{\text{d}t}
\color{red}\cancel{\color{black}{a_y(t) = 0}} m·s-1
a_x = \dfrac{\text{d}v_x(t)}{\text{d}t}
\color{red}\cancel{\color{black}{a_x(t) = - \dfrac{a}{2}}}
a_y = \dfrac{\text{d}v_y(t)}{\text{d}t}
\color{red}\cancel{\color{black}{a_y(t) = 0}} m·s-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Interprétations graphiques (1)
✔ REA/MATH : Intégrer
Le suivi temporel de la vitesse d'un point mobile \text{M} est représenté ci-dessous. Le point \text{M} est animé d'un mouvement rectiligne sur l'axe (\text{O}x). À t = 0 s, \text{M} est à l'arrêt au point d'abscisse x_0 = 0 m.

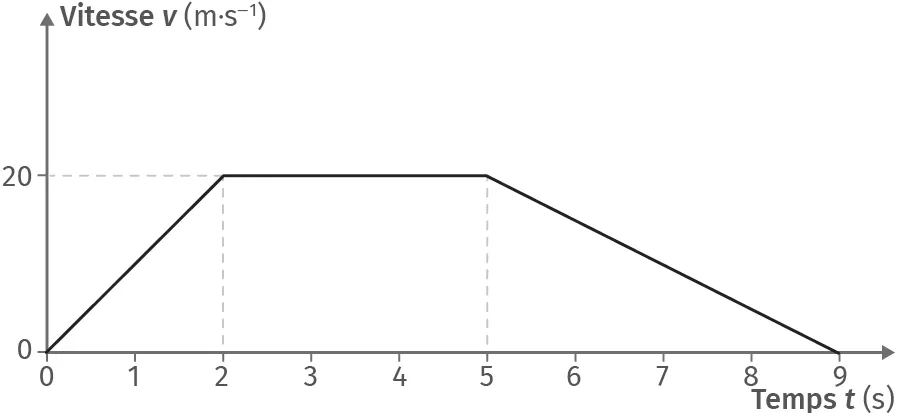


1. Caractériser le mouvement en le découpant en trois phases :
2. Pour chaque phase, déterminer :
a. l'équation horaire v(t) ;
- phase 1 : de 0 à 2 s.
- phase 2 : de 2 s à 5 s.
- phase 3 : de 5 s à 9 s.
2. Pour chaque phase, déterminer :
a. l'équation horaire v(t) ;
b. l'équation horaire de position x(t) ;
c. la distance parcourue lors de cette phase ;
d. l'aire sous la courbe de la vitesse.
3. Déduire des réponses précédentes la distance totale parcourue par le point \text{M} entre 0 s et 9 s. Comparer cette valeur avec l'aire sous la courbe.
c. la distance parcourue lors de cette phase ;
d. l'aire sous la courbe de la vitesse.
3. Déduire des réponses précédentes la distance totale parcourue par le point \text{M} entre 0 s et 9 s. Comparer cette valeur avec l'aire sous la courbe.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Interprétations graphiques (2)
✔ APP : Faire des prévisions à l'aide d'un modèle
Deux automobiles A_1 et A_2 se croisent sur une autoroute parfaitement rectiligne. Leurs coordonnées de position, notées respectivement x_1(t) et x_2(t) et exprimées en (km), sont représentées ci‑dessous :

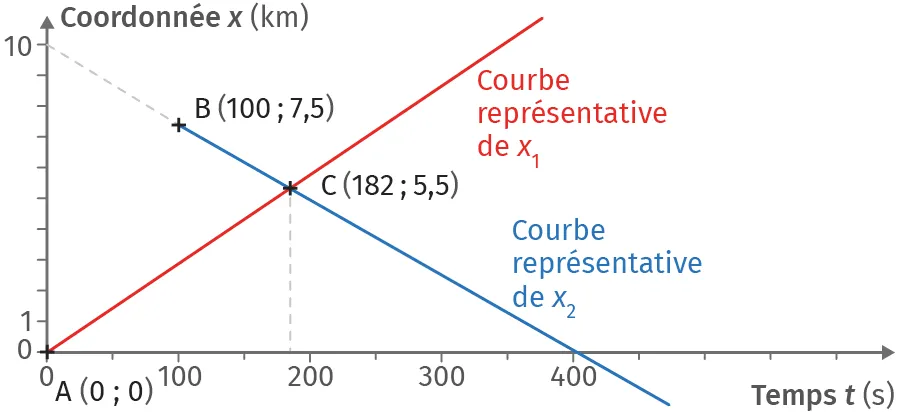
Préciser, en le justifiant, si les affirmations suivantes sont vraies ou fausses.


Préciser, en le justifiant, si les affirmations suivantes sont vraies ou fausses.
a. A_1 roule dans le sens des x croissants.
b. A_2 roule dans le sens des x décroissants.
c. À l'instant initial, A_1 et A_2 sont distantes de 10 m.
d. À l'instant initial, A_1 et A_2 sont à l'arrêt.
b. A_2 roule dans le sens des x décroissants.
c. À l'instant initial, A_1 et A_2 sont distantes de 10 m.
d. À l'instant initial, A_1 et A_2 sont à l'arrêt.
e. x_2(t) = -a \cdot t + b avec a = 25 m·s-1 et b = 10 km.
f. A_1 et A_2 ont des mouvements uniformes.
g. A_1 et A_2 se croisent environ trois minutes après le lancement du chronomètre de A_1.
h. A_1 roule à 108 km·h-1.
f. A_1 et A_2 ont des mouvements uniformes.
g. A_1 et A_2 se croisent environ trois minutes après le lancement du chronomètre de A_1.
h. A_1 roule à 108 km·h-1.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Ballon-sonde
✔ REA/MATH : Intégrer
Doc.
Définition
Un ballon-sonde est un ballon à gaz utilisé dans les domaines de la météorologie et de l'astronautique. Il s'agit d'un ballon libre non habité, utilisé pour faire des mesures locales dans l'atmosphère grâce à un certain nombre d'instruments à bord, dans une nacelle appelée radiosonde [...]. Le ballon-sonde a été inventé par Gustave Hermite en 1892.
Son principal intérêt est de pouvoir atteindre des altitudes d'au moins 35 km, le record étant de 53 km, difficile à obtenir avec des moyens plus conventionnels tels que les avions, et à un coût bien inférieur à une fusée‑sonde ou un satellite.
Son principal intérêt est de pouvoir atteindre des altitudes d'au moins 35 km, le record étant de 53 km, difficile à obtenir avec des moyens plus conventionnels tels que les avions, et à un coût bien inférieur à une fusée‑sonde ou un satellite.
« Ballon-sonde », wikipedia.org.


Lors d'un lâcher, un ballon-sonde a une vitesse verticale constante v_0 tout au long de son ascension. Le vent emporte le ballon-sonde à la vitesse horizontale v_x(t) = k \cdot z(t), proportionnelle à l'altitude du ballon.
L'étude du mouvement du centre du ballon-sonde s'effectue dans le repère galiléen (\text{O}\:,\vec{i}\:,\vec{j}).
1. Déterminer l'équation horaire z(t).
2. À l'aide de v_x(t), déterminer x(t).
3. Déterminer les composantes du vecteur accélération \vec{a}(t).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AMouvement circulaire
✔ REA/MATH : Utiliser des outils mathématiques
Un point mobile M décrit une trajectoire circulaire, de centre \text{C} (3 m ; -1 m), dont les coordonnées cartésiennes respectent les équations horaires suivantes :
Préciser, en le justifiant, si les affirmations suivantes sont vraies ou fausses.
Un point mobile M décrit une trajectoire circulaire, de centre \text{C} (3 m ; -1 m), dont les coordonnées cartésiennes respectent les équations horaires suivantes :
\overrightarrow{\text{OM}} \begin{pmatrix}
x(t) = x_\text{C} + R \cdot \cos(\omega \cdot t) \\
y(t) = y_\text{C} + R \cdot \sin(\omega \cdot t)
\end{pmatrix}_{(\text{O}, \ \overrightarrow{i}, \ \overrightarrow{j})}
Préciser, en le justifiant, si les affirmations suivantes sont vraies ou fausses.
-
a. Les conditions initiales de position sont (3 m ; -1 m).
b. La composante v_x(t) de la vitesse s'exprime selon v_x(t) = R \cdot \omega \cdot \cos(\omega \cdot t).
c. Le mouvement est uniforme.
d. La valeur de l'accélération est constante et égale à a = R \cdot \omega.
e. Le vecteur \overrightarrow{a}(t) pointe vers l'origine \text{O} du repère.
f. Si le rayon de la trajectoire circulaire est R = 2{,}0 cm et \omega = 0{,}35 rad·s-1, la valeur de la vitesse est alors égale à v = 0{,}70 m·s-1.
Données
- Intensité de la pesanteur : g = 9,81\ \text{m}\cdot\text{s}^{-2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLancer‑Franc
✔ REA/MATH : Résoudre une équation différentielle
Un basketteur effectue un lancer-franc. Au moment où le ballon quitte la main du joueur, il est à 2{,}0 m du sol, sa vitesse a une valeur v_0 et fait un angle \alpha avec l'horizontal. Au moment du lancer, le joueur est à 4{,}6 m du panier, qui se situe à une hauteur de 3{,}0 m.
L'origine du repère est prise au niveau des pieds du joueur. L'axe (O x) est horizontal, orienté positivement vers le panier, et l'axe (O z) est vertical, orienté positivement vers le haut.
On représente le ballon par un point \text{M} de coordonnées (x(t) ~; z(t)), et le panier par un point \text{P} de coordonnées (xp~; zp).
On admet que l'accélération du ballon est constante, et que le vecteur accélération est \overrightarrow{a} = \overrightarrow{g}.
L'origine du repère est prise au niveau des pieds du joueur. L'axe (O x) est horizontal, orienté positivement vers le panier, et l'axe (O z) est vertical, orienté positivement vers le haut.
On représente le ballon par un point \text{M} de coordonnées (x(t) ~; z(t)), et le panier par un point \text{P} de coordonnées (xp~; zp).
On admet que l'accélération du ballon est constante, et que le vecteur accélération est \overrightarrow{a} = \overrightarrow{g}.
1. Justifier que cette réaction permet de synthétiser des polymères.
Cliquez pour accéder à une zone de dessin
2. Exprimer v_{0x} et v_{0z} en fonction de v_0 et \alpha.
3. Justifier que x(t) correspond à une évolution affine et que z(t) correspond à une évolution parabolique au cours du temps t.
4. Donner les équations horaires de v_x, v_z, x et z.
5. Le joueur réalise un shoot avec v_0 = 7{,}8 m·s-1 et \alpha = 61 °. Va‑t‑il réussir son lancer ?
3. Justifier que x(t) correspond à une évolution affine et que z(t) correspond à une évolution parabolique au cours du temps t.
4. Donner les équations horaires de v_x, v_z, x et z.
5. Le joueur réalise un shoot avec v_0 = 7{,}8 m·s-1 et \alpha = 61 °. Va‑t‑il réussir son lancer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CMouvement de la Lune
✔ REA : Appliquer une formule
On assimile le mouvement de la Lune autour de la Terre à un mouvement circulaire uniforme.
1. Déterminer les valeurs de la vitesse et de l'accélération.
2. Exprimer les vecteurs vitesse et accélération dans le repère de Frenet.
On assimile le mouvement de la Lune autour de la Terre à un mouvement circulaire uniforme.
1. Déterminer les valeurs de la vitesse et de l'accélération.
2. Exprimer les vecteurs vitesse et accélération dans le repère de Frenet.
Données
- Distance Terre‑Lune : D = 3{,}83 \times 10^8 m
- Période de révolution de la Lune autour de la Terre : T = 27{,}3 j
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
