Activités

A

B

Soit $f$ la fonction définie sur $[0~; 1]$ par $f(x)=1-x^{2}$.
On note $\mathcal{C}_f$ sa représentation graphique. L’unité du graphique est le cm.
$\mathcal{D}$ est l’aire du domaine hachuré en bleu ci‑contre.

À l’aide du quadrillage du graphique A, estimer en cm², la valeur de $\mathcal{D}$, en donnant sa valeur approchée.


Pour la suite, on subdivise l’intervalle $[0~; 1]$ en $n$ intervalles de la forme $\left[\dfrac{k}{n} ; \dfrac{k+1}{n}\right]$, où $n$ et $k$ sont des entiers tels que $n \neq 0$ et $0 \leqslant k \leqslant n-1$ (sur le graphique B, on a représenté le cas $n = 8$).

On considère un entier $k$ tel que $0 \leqslant k \leqslant n-1$. On note $\mathrm{A}_k$ et $\mathrm{B}_k$ les aires respectives de chaque rectangle rouge et vert.
On note : $\mathrm{I}_{n}=\mathrm{A}_{0}+\mathrm{A}_{1}+\ldots+\mathrm{A}_{n-1}$ et $\mathrm{J}_{n}=\mathrm{B}_{0}+\mathrm{B}_{1}+\ldots+\mathrm{B}_{n-1}$.

a) Exprimer $\mathrm{A}_k$ et $\mathrm{B}_k$ en fonction de $n$, $f\left(\dfrac{k}{n}\right)$ et $f\left(\dfrac{k+1}{n}\right)$.


b) Pour $n \in \N^*$, on pose $u_{n}=\dfrac{1}{n}\left[f\left(\dfrac{1}{n}\right)+f\left(\dfrac{2}{n}\right)+\ldots+f(1)\right]$.
En déduire que $u_{n} \leqslant \mathcal{D} \leqslant u_{n}+\dfrac{1}{n}$.


c) La question précédente permet d’obtenir un encadrement de $\mathcal{D}$.
Déterminer l’amplitude de cet encadrement en fonction de $n$.


d) Lorsque $n$ tend vers $+\infty$, que peut‑on dire de l’amplitude de cet encadrement ? Que peut‑on en déduire pour $\mathcal{D}$ ?


À l’aide d’un tableur, on va calculer les valeurs de $\mathrm{I}_n$ et $\mathrm{J}_n$ dans le cas $n=10$.

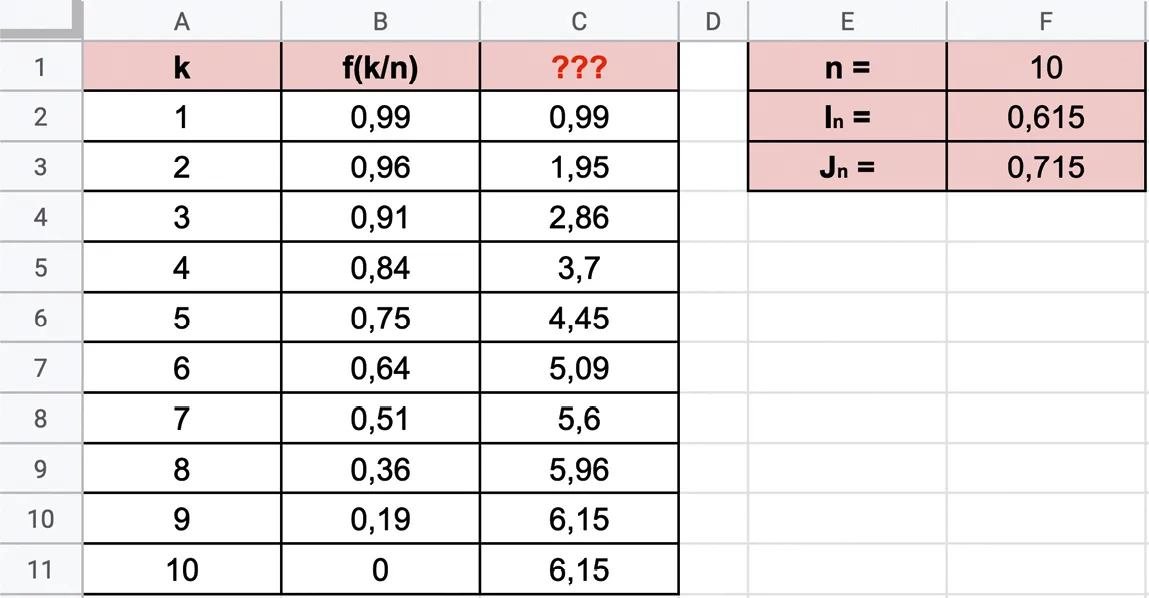
a) Quelle formule a été saisie dans la cellule B2 ?


b) Dans les cellules C2 et C3 ont été saisies respectivement les formules =B2 et =C2+B3. La cellule C3 a ensuite été copiée‑glissée jusqu’en C11. Quelle formule obtient‑on dans la cellule C11 ? Que peut‑on mettre comme intitulé dans la cellule C1 ?


c) Quelles formules ont été saisies dans les cellules F2 et F3 ?


d) Modifier la feuille de calcul pour déterminer un encadrement de $\mathcal{D}$ d’amplitude $10^{-3}$.

Soient $a$, $b$ et $x_0$ trois réels tels que $a \lt b$ et $x_{0} \in[a~; b]$.
On considère une fonction $f$ continue et positive sur $[a~; b]$ et on définit la fonction $\mathrm{F}_a$ sur $[a~; b]$ par $\mathrm{F}_{a}(x)=\displaystyle\int_{a}^{x} f(t) \mathrm{d} t$. On suppose, sans perte de généralité, que $f$ est croissante sur $[a~; b]$.

a) Pour tout réel $h > 0$ tel que $x_{0}+h\lt b$, interpréter graphiquement $\mathrm{F}_{a}\left(x_{0}+h\right)$ et $\mathrm{F}_{a}\left(x_{0}\right)$.


b) En déduire une interprétation graphique de $\mathrm{F}_{a}\left(x_{0}+h\right)-\mathrm{F}_{a}\left(x_{0}\right)$.


c) En utilisant les rectangles $\text{ABCD}$ et $\text{ABFE}$, justifier que $h f\left(x_{0}\right) \leqslant \mathrm{F}_{a}\left(x_{0}+h\right)-\mathrm{F}_{a}\left(x_{0}\right) \leqslant h f\left(x_{0}+h\right)$, puis en déduire un encadrement de $\dfrac{\mathrm{F}_{a}\left(x_{0}+h\right)-\mathrm{F}_{a}\left(x_{0}\right)}{h}$.


Recommencer la question précédente avec $h \lt 0$ tel que $x_{0}+h>a$. On fera notamment attention au sens de la double inégalité.


Quel argument permet de justifier que $\lim \limits_{\substack{h \rightarrow 0}} f\left(x_{0}+h\right)=f\left(x_{0}\right)$ ?

En utilisant des primitives, calculer les intégrales $\mathrm{J}=\displaystyle\int_{0}^{3} \mathrm{e}^{x} \mathrm{d} x$ et $\mathrm{K}=\displaystyle\int_{0}^{3} 2 x \mathrm{e}^{x^{2}+1} \mathrm{d} x$. Peut‑on calculer $\mathrm{I}=\displaystyle\int_{0}^{3} x \mathrm{e}^{x} \mathrm{d} x$ en utilisant des primitives ?


Calcul de l’intégrale $\mathbf{I}$. On définit sur $[0~; 3]$ deux fonctions $u$ et $v$ par $u(x)=\mathrm{e}^{x}$ et $v(x)=x$.
a) Déterminer la fonction dérivée de $u \times v$ sur $[0~; 3]$.


b) Intégrer l’égalité précédente sur $[0~; 3]$ puis en déduire la valeur de l’intégrale $\mathrm{I}=\displaystyle\int_{0}^{3} u^{\prime}(x) v(x) d x$.


c) Utiliser la même méthode pour calculer $\displaystyle\int_{0}^{3} x^{2} \mathrm{e}^{x} d x$.


Cas général. Soient $a$ et $b$ deux réels tels que $a \lt b$. On considère deux fonctions $u$ et $v$ dérivables sur $[a~; b]$ telles que $u'$ et $v'$ soient continues sur $[a~; b]$. Dans le cours, on démontrera que : $[(u v)(x)]_{a}^{b}=\displaystyle\int_{a}^{b}\left(u^{\prime} v\right)(x) \mathrm{d} x+\displaystyle\int_{a}^{b}\left(u v^{\prime}\right)(x) \mathrm{d} x$. En déduire une formule pour calculer $\displaystyle\int_{a}^{b}\left(u^{\prime} v\right)(x) \mathrm{d} x$.