Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 11
Analyse
L'épreuve finale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice guidé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
[D'après bac S, Amérique du sud, novembre 2019]On considère la suite (u_n) définie pour tout entier n \geqslant 0 par \left\{\begin{array}{c} u_{0}=5 \\ u_{n+1}=3-\frac{10}{u_{n}+4} \end{array}\right..
Partie A
1. Déterminer la valeur exacte de u_1 et de u_2.
2. Démontrer par récurrence que, pour tout entier naturel n, u_{n} \geqslant 1.
3. Démontrer que, pour tout entier naturel n, u_{n+1}-u_{n}=\frac{\left(1-u_{n}\right)\left(u_{n}+2\right)}{u_{n}+4}.
4. En déduire le sens de variation de la suite (u_n).
5. Justifier que la suite (u_n) converge.
1. Déterminer la valeur exacte de u_1 et de u_2.
Aide
Il suffit d'utiliser la définition de la suite (u_n).
2. Démontrer par récurrence que, pour tout entier naturel n, u_{n} \geqslant 1.
Aide
On pourra s'aider de la pour rédiger convenablement le raisonnement par récurrence.
3. Démontrer que, pour tout entier naturel n, u_{n+1}-u_{n}=\frac{\left(1-u_{n}\right)\left(u_{n}+2\right)}{u_{n}+4}.
Aide
Il faut repartir de l'expression de u_{n+1} et effectuer les
calculs fractionnaires consciencieusement.
4. En déduire le sens de variation de la suite (u_n).
Aide
Il faut déterminer le lien entre le sens de variation de
(u_n) et la question précédente.
5. Justifier que la suite (u_n) converge.
Aide
Un théorème permet de répondre convenablement en
s'appuyant sur certains résultats démontrés précédemment.
Partie B
On considère la suite (v_n) définie pour tout entier naturel n par v_{n}=\frac{u_{n}-1}{u_{n}+2}.
1. a. Démontrer que (v_n) est une suite géométrique dont on déterminera la raison et le premier terme v_0.
b. Exprimer v_n en fonction de n et en déduire que, pour tout entier naturel n, v_{n} \neq 1.
2. Démontrer que, pour tout entier naturel n, u_{n}=\frac{2 v_{n}+1}{1-v_{n}}.
3. En déduire la limite de la suite (u_n).
On considère la suite (v_n) définie pour tout entier naturel n par v_{n}=\frac{u_{n}-1}{u_{n}+2}.
1. a. Démontrer que (v_n) est une suite géométrique dont on déterminera la raison et le premier terme v_0.
Aide
Il faut essayer de retrouver l'expression d'une suite
géométrique à partir de v_{n+1}.
b. Exprimer v_n en fonction de n et en déduire que, pour tout entier naturel n, v_{n} \neq 1.
Aide
Pour la première partie de la question, on utilisera une
propriété des suites géométriques. Pour la seconde partie,
on pourra, par exemple, démontrer que v_n \lt 1, pour tout
n \in \N.
2. Démontrer que, pour tout entier naturel n, u_{n}=\frac{2 v_{n}+1}{1-v_{n}}.
Aide
Il suffit de repartir de la définition de v_n et d'effectuer
consciencieusement les calculs fractionnaires.
3. En déduire la limite de la suite (u_n).
Aide
On pourra commencer par calculer la limite de (v_n).
On considère l'algorithme ci-dessous.
\boxed{
\begin{array} { l }
u \leftarrow 5 \\
n \leftarrow 0 \\
\text {Tant que } u \geqslant 1,01 \text {, faire } : \\
\quad \quad n \leftarrow n+1 \\
\quad \quad u \leftarrow 3-\frac{10}{u+4} \\
\text {Fin tant que}
\end{array}
}
1. Après exécution de l'algorithme, quelle valeur est contenue dans la variable n ?
2. À l'aide des parties A et B, interpréter cette valeur.
Aide
Il n'est pas utile de programmer l'algorithme mais la
calculatrice est utile pour répondre à cette question.
2. À l'aide des parties A et B, interpréter cette valeur.
Aide
Quel est le lien entre cet algorithme et l'étude de la
suite (u_n) dans les parties A et B ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
[D'après bac S, Amérique du Nord, mai 2019]
Partie A : Établir une égalité
Sur l'intervalle [0 \:;+\infty], on définit la fonction f par f(x)=x-\ln (x+1).
1. Étudier le sens de variation de la fonction f sur l'intervalle [0 \:;+\infty].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
2. En déduire que, pour tout x \in [0 \:;+\infty], \ln (x+1) \leqslant x.
Partie B : Application à l'étude d'une suite
On pose u_0 = 1 et, pour tout entier naturel n, u_{n+1}=u_{n}-\ln \left(1+u_{n}\right).
On admet que la suite de terme général u_n est bien définie.
1. Calculer une valeur approchée à 10^{-3} près de u_2.
2. a. Démontrer par récurrence que, pour tout entier naturel n, u_{n} \geqslant 0.
b. Démontrer que la suite (u_n) est décroissante et en déduire que, pour tout entier naturel n, u_{n} \leqslant 1.
c. Montrer que la suite (u_n) est convergente.
3. On note \ell, la limite de la suite (u_n). Justifier que \ell vérifie \ell = f(\ell) puis déterminer sa valeur.
2. a. Démontrer par récurrence que, pour tout entier naturel n, u_{n} \geqslant 0.
b. Démontrer que la suite (u_n) est décroissante et en déduire que, pour tout entier naturel n, u_{n} \leqslant 1.
c. Montrer que la suite (u_n) est convergente.
3. On note \ell, la limite de la suite (u_n). Justifier que \ell vérifie \ell = f(\ell) puis déterminer sa valeur.
4. a. Écrire un algorithme qui, pour un entier naturel p donné, permet de déterminer le plus petit rang \text{N} à partir duquel tous les termes de la suite (u_n) sont inférieurs à 10^{-p}.
b. Déterminer le plus petit entier naturel n à partir duquel tous les termes de la suite (u_n) sont inférieurs à 10^{-15}.
b. Déterminer le plus petit entier naturel n à partir duquel tous les termes de la suite (u_n) sont inférieurs à 10^{-15}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
[D'après bac S, Nouvelle-Calédonie, novembre 2019]
On considère la fonction f définie sur [0 \:;+\infty[ par :
f(x)=\ln \left(\frac{3 x+1}{x+1}\right).
On admet que la fonction f est dérivable sur [0 \:;+\infty[ et on note f^\prime sa fonction dérivée.
On note \mathcal{C}_f la courbe représentative de la fonction f dans un repère orthogonal.
On admet que la fonction f est dérivable sur [0 \:;+\infty[ et on note f^\prime sa fonction dérivée.
On note \mathcal{C}_f la courbe représentative de la fonction f dans un repère orthogonal.
Le zoom est accessible dans la version Premium.
Partie A
1. Déterminer \lim\limits _{x \rightarrow+\infty} f(x) et en donner une interprétation graphique.
2. a. Démontrer que, pour tout nombre réel x positif ou nul, f^{\prime}(x)=\frac{2}{(x+1)(3 x+1)}.
b. En déduire que la fonction f est strictement croissante sur [0 \:;+\infty[.
Partie B
Soit (u_n) la suite définie par u_0 = 3 et, pour tout entier naturel n, u_{n+1}=f\left(u_{n}\right).
1. Démontrer par récurrence que, pour tout entier naturel n, \frac{1}{2} \leqslant u_{n+1} \leqslant u_{n}.
2. Démontrer que la suite (u_n) converge vers une limite strictement positive.
1. Déterminer \lim\limits _{x \rightarrow+\infty} f(x) et en donner une interprétation graphique.
2. a. Démontrer que, pour tout nombre réel x positif ou nul, f^{\prime}(x)=\frac{2}{(x+1)(3 x+1)}.
b. En déduire que la fonction f est strictement croissante sur [0 \:;+\infty[.
Partie B
Soit (u_n) la suite définie par u_0 = 3 et, pour tout entier naturel n, u_{n+1}=f\left(u_{n}\right).
1. Démontrer par récurrence que, pour tout entier naturel n, \frac{1}{2} \leqslant u_{n+1} \leqslant u_{n}.
2. Démontrer que la suite (u_n) converge vers une limite strictement positive.
Partie C
On note \ell la limite de la suite (u_n).
On admet que f(\ell)=\ell.
L'objectif de cette partie est de déterminer une valeur approchée de \ell.
On introduit pour cela la fonction g définie sur [0 \:;+\infty[ par g(x) = f(x) - x.
On donne ci-dessous le tableau de variations de la fonction g sur [0 \:;+\infty[ où x_{0}=\frac{-2+\sqrt{7}}{3} \approx 0,215 et g\left(x_{0}\right) \approx 0,088, en arrondissant à 10^{-3} près.
1. Démontrer que l'équation g(x) = 0 admet une unique solution strictement positive. On la note \alpha.
2. a. Compléter l'algorithme ci-dessous afin que la dernière valeur prise par la variable x soit une valeur approchée de \alpha par excès à 0{,}01 près.
b. Donner alors la dernière valeur prise par la variable x lors de l'exécution de l'algorithme.
3. En déduire une valeur approchée à 0{,}01 près de la limite \ell de la suite (u_n).
On note \ell la limite de la suite (u_n).
On admet que f(\ell)=\ell.
L'objectif de cette partie est de déterminer une valeur approchée de \ell.
On introduit pour cela la fonction g définie sur [0 \:;+\infty[ par g(x) = f(x) - x.
On donne ci-dessous le tableau de variations de la fonction g sur [0 \:;+\infty[ où x_{0}=\frac{-2+\sqrt{7}}{3} \approx 0,215 et g\left(x_{0}\right) \approx 0,088, en arrondissant à 10^{-3} près.
Le zoom est accessible dans la version Premium.
1. Démontrer que l'équation g(x) = 0 admet une unique solution strictement positive. On la note \alpha.
2. a. Compléter l'algorithme ci-dessous afin que la dernière valeur prise par la variable x soit une valeur approchée de \alpha par excès à 0{,}01 près.
\boxed{
\begin{array} { l }
x \leftarrow 0{,}22 \\
\text {Tant que } ... \text { faire } : \\
\quad \quad x \leftarrow x+0{,}01 \\
\text {Fin tant que}
\end{array}
}
b. Donner alors la dernière valeur prise par la variable x lors de l'exécution de l'algorithme.
3. En déduire une valeur approchée à 0{,}01 près de la limite \ell de la suite (u_n).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
[D'après bac S, Métropole, juin 2016]]
Partie A
Soit f la fonction définie sur \R par f(x)=x-\ln \left(x^{2}+1\right).
1. Résoudre dans \R l'équation f(x) = x.
2. Déterminer la limite de la fonction f en -\infty.
Pour la suite, on admet que la limite de f en +\infty est +\infty.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
b. Montrer que, pour tout réel x appartenant à l'intervalle [0 \:; 1], f(x) appartient à [0 \:; 1].
4. On considère l'algorithme suivant.
\boxed{
\begin{array} { l }
\text{A} \leftarrow 100 \\
\text{N} \leftarrow 0 \\
\text {Tant que } \mathrm{N}-\ln \left(\mathrm{N}^{2}+1\right) \lt \mathrm{A} : \\
\quad \quad \text{N} \leftarrow \text{N}+1 \\
\text {Fin tant que}
\end{array}
}
Quelle valeur contient la variable \text{N} à la fin de l'algorithme ?
Partie B
Soit (u_n) la suite définie par u_0 = 1 et, pour tout entier naturel n, u_{n+1}=u_{n}-\ln \left(u_{n}^{2}+1\right).
1. Montrer par récurrence que, pour tout entier naturel n, un appartient à [0 \:; 1].
2. Étudier les variations de la suite (u_n).
2. Étudier les variations de la suite (u_n).
3. Montrer que la suite (u_n) est convergente.
4. On note \ell la limite de la suite (u_n). Justifier que \ell vérifie f(\ell)=\ell puis déterminer sa valeur.
4. On note \ell la limite de la suite (u_n). Justifier que \ell vérifie f(\ell)=\ell puis déterminer sa valeur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
[D'après bac S, Centres étrangers, juin 2019]]
Le but de cet exercice est d'étudier la suite (u_n) définie par la donnée de son premier terme u_1 et, pour tout entier naturel n supérieur ou égal à 1, u_{n+1}=(n+1) u_{n}-1.
Partie A
1. En détaillant le calcul, vérifier que si u_1 = 0, alors u_4 = -17.
2. Recopier et compléter l'algorithme ci-dessous pour qu'en saisissant préalablement dans \text{U} une valeur de u_1, il calcule les termes de la suite (u_n) de u_2 à u_{13}.
3. On a exécuté cet algorithme pour u_1 = 0{,}7 puis pour u_1 = 0{,}8. Voici les valeurs obtenues :
Quelle semble être la limite de cette suite si u_1 = 0{,}7 ? Et si u_1 = 0{,}8 ?
1. En détaillant le calcul, vérifier que si u_1 = 0, alors u_4 = -17.
2. Recopier et compléter l'algorithme ci-dessous pour qu'en saisissant préalablement dans \text{U} une valeur de u_1, il calcule les termes de la suite (u_n) de u_2 à u_{13}.
\boxed{
\begin{array} { l }
\text {Pour N allant de 1 à 12 : }\\
\quad \quad \text{U} \leftarrow ...\\
\text {Fin tant que}
\end{array}
}
3. On a exécuté cet algorithme pour u_1 = 0{,}7 puis pour u_1 = 0{,}8. Voici les valeurs obtenues :
| Pour \boldsymbol{u_{1}=0{,}7} | Pour \boldsymbol{u_{1}=0{,}8} |
| 0{,}4 | 0{,}6 |
| 0{,}2 | 0{,}8 |
| -0{,}2 | 2{,}2 |
| -2 | 10 |
| -13 | 59 |
| -92 | 412 |
| -737 | 3\:295 |
| -6\:634 | 29\:654 |
| -66\:341 | 296\:539 |
| -729\:752 | 3\:261\:928 |
| -8\:757\:025 | 39\:143\:135 |
| -113\:841\:326 | 508\:860\:754 |
Quelle semble être la limite de cette suite si u_1 = 0{,}7 ? Et si u_1 = 0{,}8 ?
Partie B
On considère la suite (\text{I}_n), définie pour tout entier naturel n, supérieur ou égal à 1, par : \mathrm{I}_{n}=\displaystyle\int_{0}^{1} x^{n} \mathrm{e}^{1-x} \mathrm{d} x.
On considère également la fonction \text{F} définie sur l'intervalle [0\: ; 1] par \mathrm{F}(x)=(-1-x) \mathrm{e}^{1-x} et la fonction f définie sur l'intervalle [0\: ; 1] par f(x)=x \mathrm{e}^{1-x}.
1. Prouver que la fonction \text{F} est une primitive sur l'intervalle [0\: ; 1] de la fonction f.
2. En déduire que \text{I}_{1}=\mathrm{e}-2.
3. a. Montrer, à l'aide d'une intégration par parties que, pour tout entier naturel n supérieur ou égal à 1, on a : \mathrm{I}_{n+1}=(n+1) \mathrm{I}_{n}-1.
b. En déduire la valeur de \text{I}_2.
4. a. Justifier que, pour tout nombre réel x de l'intervalle [0 \:; 1] et pour tout entier naturel n supérieur ou égal à 1, on a : 0 \leqslant x^{n} \mathrm{e}^{1-x} \leqslant x^{n} \mathrm{e}.
b. En déduire que, pour tout entier naturel n supérieur ou égal à 1, on a : 0 \leqslant \mathrm{I}_{n} \leqslant \frac{\mathrm{e}}{n+1}.
c. Déterminer la limite de la suite (\mathrm{I}_{n}).
On considère la suite (\text{I}_n), définie pour tout entier naturel n, supérieur ou égal à 1, par : \mathrm{I}_{n}=\displaystyle\int_{0}^{1} x^{n} \mathrm{e}^{1-x} \mathrm{d} x.
On considère également la fonction \text{F} définie sur l'intervalle [0\: ; 1] par \mathrm{F}(x)=(-1-x) \mathrm{e}^{1-x} et la fonction f définie sur l'intervalle [0\: ; 1] par f(x)=x \mathrm{e}^{1-x}.
1. Prouver que la fonction \text{F} est une primitive sur l'intervalle [0\: ; 1] de la fonction f.
2. En déduire que \text{I}_{1}=\mathrm{e}-2.
3. a. Montrer, à l'aide d'une intégration par parties que, pour tout entier naturel n supérieur ou égal à 1, on a : \mathrm{I}_{n+1}=(n+1) \mathrm{I}_{n}-1.
b. En déduire la valeur de \text{I}_2.
4. a. Justifier que, pour tout nombre réel x de l'intervalle [0 \:; 1] et pour tout entier naturel n supérieur ou égal à 1, on a : 0 \leqslant x^{n} \mathrm{e}^{1-x} \leqslant x^{n} \mathrm{e}.
b. En déduire que, pour tout entier naturel n supérieur ou égal à 1, on a : 0 \leqslant \mathrm{I}_{n} \leqslant \frac{\mathrm{e}}{n+1}.
c. Déterminer la limite de la suite (\mathrm{I}_{n}).
Dans cette partie, on note n! le nombre défini pour tout entier naturel n supérieur ou égal à 1, par : 1! = 1 ; 2 !=2 \times 1 ; et \sin \geqslant 3: n !=n \times(n-1) \times \ldots \times 1.
Plus généralement, on a, pour tout entier naturel n supérieur ou égal à 1 : (n+1) !=(n+1) \times n !.
1. Démontrer par récurrence que, pour tout entier naturel n supérieur ou égal à 1, on a : u_{n}=n !\left(u_{1}-\mathrm{e}+2\right)+\mathrm{I}_{n}.
2. On admet que \lim\limits_{n \rightarrow+\infty} n !=+\infty.
a. Déterminer la limite de la suite (u_n) lorsque u_{1}=0,7.
b. Déterminer la limite de la suite (u_n) lorsque u_{1}=0,8.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
[D'après bac S, Antilles-Guyane, septembre 2017]
Partie A
Soit f la fonction définie et dérivable sur [1 \:;+\infty[ telle que, pour tout nombre réel x supérieur ou égal à 1 : f(x)=\frac{1}{x} \ln (x). On note \mathcal{C} la courbe représentative de f dans un repère orthonormé.
1. Démontrer que la courbe \mathcal{C} admet une asymptote horizontale.
2. Déterminer la fonction dérivée f^\prime de la fonction f sur l'intervalle [1 \:;+\infty[.
3. Étudier les variations de la fonction f sur [1 \:;+\infty[.
Soit f la fonction définie et dérivable sur [1 \:;+\infty[ telle que, pour tout nombre réel x supérieur ou égal à 1 : f(x)=\frac{1}{x} \ln (x). On note \mathcal{C} la courbe représentative de f dans un repère orthonormé.
1. Démontrer que la courbe \mathcal{C} admet une asymptote horizontale.
2. Déterminer la fonction dérivée f^\prime de la fonction f sur l'intervalle [1 \:;+\infty[.
3. Étudier les variations de la fonction f sur [1 \:;+\infty[.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Partie B
On considère la suite (u_n) définie pour tout entier naturel n par u_{n}=\displaystyle\int_{1}^{2} \frac{1}{x^{n+1}} \ln (x) \mathrm{d} x.
1. Démontrer que u_{0}=\frac{1}{2}[\ln (2)]^{2}. Interpréter graphiquement ce résultat.
2. Prouver que, pour tout entier naturel n et pour tout nombre réel x de l'intervalle [1 \:; 2], on a : 0 \leqslant \frac{1}{x^{n+1}} \ln (x) \leqslant \frac{1}{x^{n+1}} \ln (2).
3. En déduire que, pour tout entier naturel n, on a : 0 \leqslant u_{n} \leqslant \frac{\ln (2)}{n}\left(1-\frac{1}{2^{n}}\right).
4. Déterminer la limite de la suite (u_n).
On considère la suite (u_n) définie pour tout entier naturel n par u_{n}=\displaystyle\int_{1}^{2} \frac{1}{x^{n+1}} \ln (x) \mathrm{d} x.
1. Démontrer que u_{0}=\frac{1}{2}[\ln (2)]^{2}. Interpréter graphiquement ce résultat.
2. Prouver que, pour tout entier naturel n et pour tout nombre réel x de l'intervalle [1 \:; 2], on a : 0 \leqslant \frac{1}{x^{n+1}} \ln (x) \leqslant \frac{1}{x^{n+1}} \ln (2).
3. En déduire que, pour tout entier naturel n, on a : 0 \leqslant u_{n} \leqslant \frac{\ln (2)}{n}\left(1-\frac{1}{2^{n}}\right).
4. Déterminer la limite de la suite (u_n).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
[D'après bac S, Amérique du Nord, mai 2018]
Partie A
On considère la fonction f définie sur [2 \:; 10] par : f(x)=x-2+2 \ln \left(\frac{2}{x}\right).
1. Justifier que la fonction f est dérivable sur [2 \:; 10] et déterminer l'expression de sa dérivée f^\prime.
2. Dresser le tableau de variations de f sur [2 \:; 10].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
3. Montrer qu'il existe un unique réel \alpha dans l'intervalle [2 \:; 10] tel que f(\alpha) = 1{,}6.
4. Donner une valeur approchée à 10^{-2} près de \alpha.
Partie B
Lors d'une expérience en laboratoire, on lance un projectile dans un milieu fluide. L'objectif est de déterminer pour quel angle de tir \theta par rapport à l'horizontale la hauteur du projectile ne dépasse pas 1{,}6 mètre.
On modélise ici le projectile par un point qui se déplace, dans un plan vertical, sur la courbe représentative de la fonction f définie sur l'intervalle [0 \:; 1[ par g(x)=b x+2 \ln (1-x), où b est un paramètre réel supérieur ou égal à 2, x est l'abscisse du projectile, et g(x) son ordonnée, toutes les deux exprimées en mètre.
On modélise ici le projectile par un point qui se déplace, dans un plan vertical, sur la courbe représentative de la fonction f définie sur l'intervalle [0 \:; 1[ par g(x)=b x+2 \ln (1-x), où b est un paramètre réel supérieur ou égal à 2, x est l'abscisse du projectile, et g(x) son ordonnée, toutes les deux exprimées en mètre.
Le zoom est accessible dans la version Premium.
1. La fonction g est dérivable sur l'intervalle [0 \:; 1[.
On note g^\prime sa dérivée. Montrer que, pour tout réel x de
l'intervalle [0 \:; 1[, on a g^{\prime}(x)=\frac{-b x+b-2}{1-x}.
2. On admet que la fonction g possède un maximum sur l'intervalle [0 \:; 1[. Montrer que ce maximum est égal à b-2+2 \ln \left(\frac{2}{b}\right).
3. Déterminer pour quelles valeurs du paramètre b la hauteur maximale du projectile ne dépasse pas 1{,}6 mètre.
4. Dans cette question, on choisit b = 5{,}69. L'angle de tir \theta correspond à l'angle entre l'axe des abscisses et la tangente à la courbe de la fonction g au point d'abscisse 0. Déterminer une valeur approchée au dixième de degré près de l'angle \theta.
2. On admet que la fonction g possède un maximum sur l'intervalle [0 \:; 1[. Montrer que ce maximum est égal à b-2+2 \ln \left(\frac{2}{b}\right).
3. Déterminer pour quelles valeurs du paramètre b la hauteur maximale du projectile ne dépasse pas 1{,}6 mètre.
4. Dans cette question, on choisit b = 5{,}69. L'angle de tir \theta correspond à l'angle entre l'axe des abscisses et la tangente à la courbe de la fonction g au point d'abscisse 0. Déterminer une valeur approchée au dixième de degré près de l'angle \theta.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
[D'après bac S, Antilles-Guyane, juin 2018]
Un publicitaire souhaite imprimer le logo ci-dessous sur
un T-shirt.
Il dessine ce logo à l'aide des courbes de deux fonctions f et g définies sur \R par :
f(x)=\mathrm{e}^{-x}(-\cos (x)+\sin (x)+1) et g(x)=-\mathrm{e}^{-x} \cos (x).
Il dessine ce logo à l'aide des courbes de deux fonctions f et g définies sur \R par :
f(x)=\mathrm{e}^{-x}(-\cos (x)+\sin (x)+1) et g(x)=-\mathrm{e}^{-x} \cos (x).
Le zoom est accessible dans la version Premium.
Partie A
1. Justifier que, pour tout x \in \mathbb{R}:-\mathrm{e}^{-x} \leqslant f(x) \leqslant 3 \mathrm{e}^{-x}.
2. En déduire la limite de f en +\infty.
3. a. Justifier que la fonction f est dérivable sur \R.
b. On note f^\prime la fonction dérivée de f. Montrer que, pour tout x \in \R : f^{\prime}(x)=\mathrm{e}^{-x}(2 \cos (x)-1).
4. Dans cette question, on étudie la fonction f sur l'intervalle [-\pi \: ; \pi].
a. Déterminer le signe de f^{\prime}(x), pour x appartenant à l'intervalle[-\pi \: ; \pi].
b. En déduire les variations de f sur [-\pi \: ; \pi].
1. Justifier que, pour tout x \in \mathbb{R}:-\mathrm{e}^{-x} \leqslant f(x) \leqslant 3 \mathrm{e}^{-x}.
2. En déduire la limite de f en +\infty.
3. a. Justifier que la fonction f est dérivable sur \R.
b. On note f^\prime la fonction dérivée de f. Montrer que, pour tout x \in \R : f^{\prime}(x)=\mathrm{e}^{-x}(2 \cos (x)-1).
4. Dans cette question, on étudie la fonction f sur l'intervalle [-\pi \: ; \pi].
a. Déterminer le signe de f^{\prime}(x), pour x appartenant à l'intervalle[-\pi \: ; \pi].
b. En déduire les variations de f sur [-\pi \: ; \pi].
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Partie B
On note \mathcal{C}_f et \mathcal{C}_g les représentations graphiques des fonctions f et g dans un repère orthonormé (\text{O} \:; \vec{i}, \vec{j}). L'unité graphique est de 2 centimètres.
1. Étudier la position relative de la courbe \mathcal{C}_f par rapport à la courbe \mathcal{C}_g sur \R.
2. Soit \text{H} la fonction définie sur \R par : \text{H}(x)=\left(-\frac{\cos (x)}{2}-\frac{\sin (x)}{2}-1\right) \text{e}^{-x}.
Montrer que \text{H} est une primitive de la fonction x \mapsto(\sin x+1) e^{-x} sur \R.
3. On note \mathcal{D} le domaine délimité par la courbe \mathcal{C}_f, la courbe \mathcal{C}_g et les droites d'équation x=-\frac{\pi}{2} et x=\frac{3 \pi}{2}. Calculer, en unité d'aire, l'aire du domaine \mathcal{D}, puis en donner une valeur approchée à 10^{-2} près en cm2.
On note \mathcal{C}_f et \mathcal{C}_g les représentations graphiques des fonctions f et g dans un repère orthonormé (\text{O} \:; \vec{i}, \vec{j}). L'unité graphique est de 2 centimètres.
Le zoom est accessible dans la version Premium.
1. Étudier la position relative de la courbe \mathcal{C}_f par rapport à la courbe \mathcal{C}_g sur \R.
2. Soit \text{H} la fonction définie sur \R par : \text{H}(x)=\left(-\frac{\cos (x)}{2}-\frac{\sin (x)}{2}-1\right) \text{e}^{-x}.
Montrer que \text{H} est une primitive de la fonction x \mapsto(\sin x+1) e^{-x} sur \R.
3. On note \mathcal{D} le domaine délimité par la courbe \mathcal{C}_f, la courbe \mathcal{C}_g et les droites d'équation x=-\frac{\pi}{2} et x=\frac{3 \pi}{2}. Calculer, en unité d'aire, l'aire du domaine \mathcal{D}, puis en donner une valeur approchée à 10^{-2} près en cm2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
[D'après bac S, Métropole, juin 2005]
Partie A
Soit f la fonction définie sur \R par f(x)=\frac{3 \text{e}^{\normalsize\tfrac{x}{4}}}{2+\text{e}^{\normalsize\tfrac{x}{4}}}.
1. Démontrer que f(x)=\frac{3}{1+2\text{e}^{\normalsize-\tfrac{x}{4}}}.
2. Étudier les limites de la fonction f en +\infty et -\infty.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
Partie B
1. On a étudié en laboratoire l'évolution d'une population de petits rongeurs. La taille de la population, au temps t, est notée g(t). On définit ainsi une fonction g sur [0 \:;+\infty[ à valeurs dans \R.
La variable t désigne le temps, exprimé en année.
L'unité choisie pour g(t) est la centaine d'individus. Le modèle utilisé pour décrire cette évolution consiste à prendre pour g une solution, sur l'intervalle [0 \:;+\infty[, de l'équation différentielle \left(\mathrm{E}_{1}\right) \, : \, y^{\prime}=\frac{1}{4} y.
a. Résoudre l'équation différentielle (\text{E}_1).
b. Déterminer l'expression de g(t) lorsque, à la date t = 0, la population comprend 100 rongeurs.
c. Après combien d'années la population dépassera-telle 300 rongeurs pour la première fois ?
La variable t désigne le temps, exprimé en année.
L'unité choisie pour g(t) est la centaine d'individus. Le modèle utilisé pour décrire cette évolution consiste à prendre pour g une solution, sur l'intervalle [0 \:;+\infty[, de l'équation différentielle \left(\mathrm{E}_{1}\right) \, : \, y^{\prime}=\frac{1}{4} y.
a. Résoudre l'équation différentielle (\text{E}_1).
b. Déterminer l'expression de g(t) lorsque, à la date t = 0, la population comprend 100 rongeurs.
c. Après combien d'années la population dépassera-telle 300 rongeurs pour la première fois ?
2. En réalité, dans un secteur observé d'une région donnée, un prédateur empêche une telle croissance en tuant un certain nombre de rongeurs. On note u(t) le nombre de rongeur encore vivants au temps t (exprimé en année) dans cette région, et on admet que la fonction u, ainsi définie, vérifie (\text{E}_2) : u(0) = 1 et pour tout nombre réel t positif ou nul, u^{\prime}(t)=\frac{1}{4} u(t)-\frac{1}{12} u(t)^{2}.
a. On suppose que, pour tout réel positif t, on a u(t)\gt0. On considère, sur l'intervalle [0 \:;+\infty], la fonction h définie par h =\frac{1}{u}.
Démontrer que la fonction u est solution de \left(\mathrm{E}_{2}\right) si, et seulement si, la fonction h est solution de \left(\mathrm{E}_{3}\right): h(0)=1 et pour tout nombre réel t positif ou nul, h^{\prime}(t)=-\frac{1}{4} h(t)+\frac{1}{12}.
b. Donner les solutions de l'équation différentielle y^{\prime}=-\frac{1}{4} y+\frac{1}{12} et en déduire l'expression de la fonction h, puis celle de la fonction u.
c. Dans ce modèle, comment se comporte la taille de la population étudiée lorsque t tend vers +\infty ? Justifier.
a. On suppose que, pour tout réel positif t, on a u(t)\gt0. On considère, sur l'intervalle [0 \:;+\infty], la fonction h définie par h =\frac{1}{u}.
Démontrer que la fonction u est solution de \left(\mathrm{E}_{2}\right) si, et seulement si, la fonction h est solution de \left(\mathrm{E}_{3}\right): h(0)=1 et pour tout nombre réel t positif ou nul, h^{\prime}(t)=-\frac{1}{4} h(t)+\frac{1}{12}.
b. Donner les solutions de l'équation différentielle y^{\prime}=-\frac{1}{4} y+\frac{1}{12} et en déduire l'expression de la fonction h, puis celle de la fonction u.
c. Dans ce modèle, comment se comporte la taille de la population étudiée lorsque t tend vers +\infty ? Justifier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
[D'après bac S, Pondichéry, mai 2018]
Dans une usine, un four cuit des céramiques à une température de 1 000 °C. À la fin de la cuisson, il est éteint et refroidit.
On s'intéresse à la phase de refroidissement du four, qui débute dès l'instant où il est éteint. La température du four est exprimée en degré Celsius (°C).
La porte du four peut être ouverte sans risque pour les céramiques dès que sa température est inférieure à 70 °C. On note t le temps (en heure) écoulé depuis l'instant correspondant à l'extinction du four.
On admet que la température du four à l'instant t est donnée par la fonction f définie sur l'intervalle [0\: ;+\infty[ et solution de l'équation différentielle (\text{E}) : y^{\prime}=-\frac{1}{5} y+4.
1. a. Résoudre l'équation différentielle \text{(E)}.
b. En déduire l'expression de la fonction f.
a. Déterminer la limite de f lorsque t tend vers +\infty.
b. Étudier les variations de la fonction f sur [0\: ;+\infty[. En déduire son tableau de variations complet.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
c. Après combien de minutes le four peut-il être ouvert sans risque pour les céramiques ?
3. Dans cette question, on s'intéresse à la baisse de la température du four au cours d'une heure, soit entre deux instants t et t + 1.
Elle est donnée par la fonction d définie pour tout nombre réel t positif par : d(t)=f(t)-f(t+1).
a. Vérifier que, pour tout nombre réel t positif : d(t)=980\left(1-\mathrm{e}^{-\normalsize\tfrac{1}{5}}\right) \mathrm{e}^{-\normalsize\tfrac{t}{5}}.
b. Déterminer la limite de d(t) lorsque t tend vers +\infty. Quelle interprétation peut-on en donner ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
[D'après bac S, Métropole, juin 2010]
Partie A
On considère l'équation différentielle (\mathrm{E}): y^{\prime}+y=\mathrm{e}^{-x}.
1. Montrer que la fonction u définie pour tout nombre réel x par u(x)=x \mathrm{e}^{-x} est une solution de l'équation différentielle (\mathrm{E}).
2. On considère l'équation différentielle \left(\mathrm{E}^{\prime}\right): y^{\prime}+y=0. Résoudre l'équation différentielle \left(\mathrm{E}^{\prime}\right).
3. Soit v une fonction définie et dérivable sur \R. Montrer que la fonction v est une solution de l'équation différentielle \left(\mathrm{E}\right) si, et seulement si, la fonction v - u est solution de l'équation différentielle \left(\mathrm{E}^{\prime}\right).
4. En déduire toutes les solutions de l'équation différentielle \left(\mathrm{E}\right).
5. Déterminer l'unique solution g de l'équation différentielle \text{(E)} telle que g(0) = 2.
Partie B
On considère la fonction f_k définie pour tout nombre réel x par f_{k}(x)=(x+k) \mathrm{e}^{-x}, où k est un nombre réel donné. On note \mathcal{C}_k la courbe représentative de la fonction f_k dans un repère orthogonal.
1. Montrer que la fonction f_k admet un maximum en x_{0}=1-k.
2. On note \text{M}_k le point de la courbe \mathcal{C}_k d'abscisse 1 - k. Montrer que le point \text{M}_k appartient à la courbe \mathcal{C} d'équation y=\text{e}^{-x}.
3. Sur le graphique ci-dessous, le repère (\text{O} \: ; \vec{i}, \vec{j}) est orthogonal et deux courbes sont tracées :
- La courbe \Gamma d'équation y=\text{e}^{-x} ;
- La courbe \mathcal{C}_k d'équation y=(x+k) \mathrm{e}^{-x}, pour un certain nombre réel k donné.
Le zoom est accessible dans la version Premium.
a. Identifier les courbes en justifiant.
b. À l'aide du graphique, déterminer la valeur du nombre réel k.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12
[D'après bac S, Pondichéry, avril 2006]
Un laboratoire de recherche étudie l'évolution d'une population animale qui semble en voie de disparition. Durant l'année 2000, une étude a été réalisée sur un échantillon de cette population, dont l'effectif initial s'élevait à 1\:000.
Cet échantillon évolue et son effectif, exprimé en millier d'individus, est approché par une fonction f du temps t (exprimé en année à partir de l'origine 2000).
D'après le modèle d'évolution choisi, la fonction f est dérivable, strictement positive sur [0 \:;+\infty[, et satisfait l'équation différentielle (\mathrm{E}): y^{\prime}=-\frac{1}{20} y(3-\ln (y)).
1. Démontrer l'équivalence suivante : « une fonction f, dérivable et strictement positive sur [0 \:;+\infty[, vérifie pour tout t de [0 \:;+\infty[, f^{\prime}(t)=-\frac{1}{20} f(t)[3-\ln \left(f(t)\right)] si, et seulement si, la fonction g=\ln (f) vérifie, pour tout t de [0 \:;+\infty[, g^{\prime}(t)=\frac{1}{20} g(t)-\frac{3}{20}. »
2. a. Donner la solution générale de l'équation différentielle z^{\prime}=\frac{1}{20} z-\frac{3}{20}.
b. En déduire qu'il existe un réel \text{C} tel que, pour tout t de [0 \:;+\infty[, f(t)=\exp\left[3+\text{C}\operatorname{exp}\left(\frac{t}{20}\right)\right].
c. En déduire la valeur de \text{C}.
3. Pour la suite, on admet que la fonction f est définie par f(t)=\exp \left[3-3 \exp \left(\frac{t}{20}\right)\right].
a. Déterminer la limite de la fonction f en +\infty.
b. Déterminer le sens de variation de f sur [0 \:;+\infty[.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
c. Résoudre dans [0 \:;+\infty[ l'inéquation f(t)\lt0{,}02. Au bout de combien d'années, selon ce modèle, la taille de l'échantillon sera-t-elle inférieure à vingt individus ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
[D'après bac ES, Asie, juin 2019]
On a représenté ci-dessous, la courbe \mathcal{C} représentative
d'une fonction f définie et dérivable sur [0{,}5 \:; 12], la
tangente \text{T}_1 à \mathcal{C} au point \text{A} d'abscisse 1 et la tangente \text{T}_2 à \mathcal{C} au point \text{B} d'abscisse 2. La tangente \text{T}_1 est parallèle à l'axe des abscisses.
Le zoom est accessible dans la version Premium.
1. a. Par lecture graphique, déterminer f^{\prime}(1) et les éventuels points d'inflexion de \mathcal{C}.
b. Encadrer \displaystyle\int_{6}^{8} f(x) \mathrm{d} x par deux entiers consécutifs.
a. Montrer que, pour tout x \in[0{,}5\: ; 12], f^{\prime}(x)=\frac{x-1}{x^{2}}.
b. Déterminer le signe de f^{\prime}(x) et en déduire le tableau de variations de f.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
3. À l'aide d'un logiciel de calcul formel, on a obtenu les
résultats suivants que l'on pourra admettre :
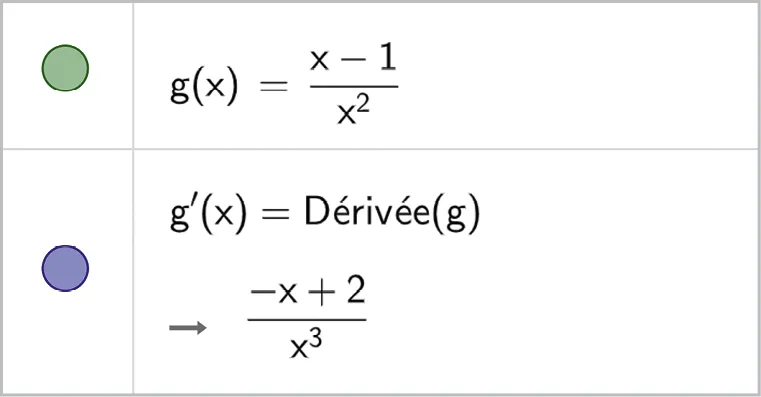
Déterminer par le calcul le plus grand intervalle sur lequel f est concave.
Le zoom est accessible dans la version Premium.
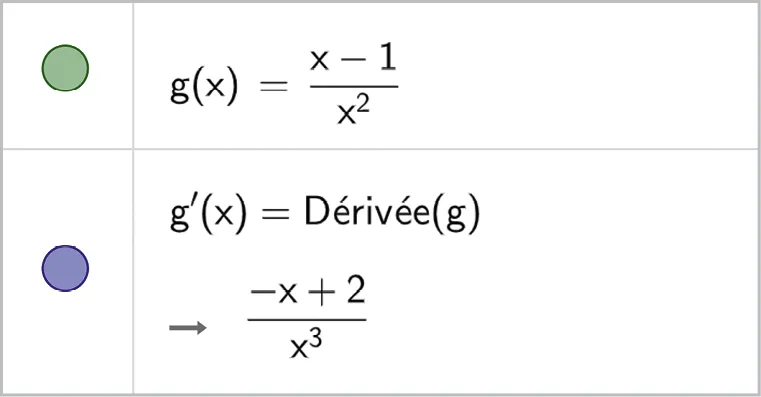
Déterminer par le calcul le plus grand intervalle sur lequel f est concave.
4. Soit \text{F} la fonction définie sur [0{,}5\: ; 12] par : \mathrm{F}(x)=(x+1) \ln (x)-x.
a. Vérifier que \text{F} est une primitive de f sur [0{,}5\: ; 12].
b. En déduire la valeur arrondie au centième de la valeur moyenne de f sur l'intervalle [0{,}5\: ; 12].
a. Vérifier que \text{F} est une primitive de f sur [0{,}5\: ; 12].
b. En déduire la valeur arrondie au centième de la valeur moyenne de f sur l'intervalle [0{,}5\: ; 12].
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah