Calcul approché d'une intégrale par la méthode des milieux

Soit f la fonction définie sur [0~; 1] par f(x)=\frac{x}{\sqrt{1+x^{2}}}. On note \mathcal{C} sa représentation graphique dans un repère orthogonal. \mathcal{D} est l'aire du domaine délimité par \mathcal{C}, l'axe des abscisses et les droites d'équation x=0 et x=1.
On subdivise l'intervalle [0~;1] en n intervalles de la forme \left[\frac{k}{n}~; \frac{k+1}{n}\right], où n et k sont des entiers tels que 1 \leqslant n \leqslant 100 et 0 \leqslant k \leqslant n-1 (sur le graphique n=10). On construit alors n rectangles de largueur \frac{1}{n} et de hauteur \frac{1}{n} f\left(\frac{\frac{k}{n}+\frac{k+1}{n}}{2}\right).
On note \mathcal{C}_k l'aire de chaque rectangle bleu et \mathrm{A}=\mathrm{C}_{0}+\mathrm{C}_{1}+\ldots+\mathrm{C}_{n-1}.

1. Reproduire la feuille de calcul suivante.

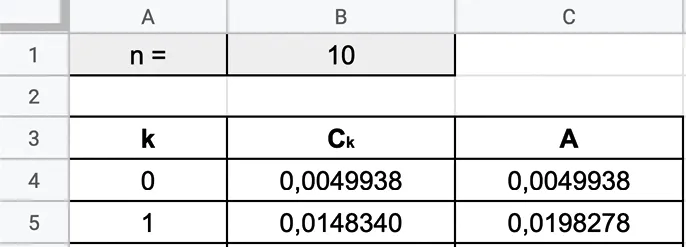2. a. Quelle formule permet d'obtenir la valeur en B4 ? La valeur en C4 ?

b. Jusqu'à quelle ligne doit‑on étirer la formule en B4 pour obtenir toutes les valeurs de \mathrm{C}_k pour n=10 ?

3. a. Pourquoi, en C5, doit‑on saisir =C4+B5 ?

b. En déduire une valeur approchée de \mathcal{D}, puis de \sqrt{2} à 10^{-3} près.

4. Avec n=100, déterminer une valeur approchée de \sqrt{2} à 10^{-5} près.

On considère l'algorithme suivant.

\boxed{ \begin{array} { l } { \text { Fonction Aire}(n):} \\ \quad \text A\leftarrow\frac{1}{n} \times \frac{1}{\sqrt{4 n^{2}+1}} \\ \quad \quad \text { Pour } k \text { allant de ... à ... } : \\ \quad \quad \quad \text A\leftarrow \\ \quad \quad \text { Fin Pour } \\ \quad \text { Retourner A } \\ \text {Fin Fonction} \end{array} }

1. Expliquer la 2^e ligne de cet algorithme, puis le compléter afin qu'il retourne la valeur de \mathrm{A} pour une valeur de n donnée.

2. Programmer et tester cet algorithme avec Python pour obtenir une valeur approchée de \mathcal{D} avec n=10 puis n=100. En déduire une valeur approchée de \sqrt{2} à 10^{-3} et à 10^{-5} près.