Fiche méthode 1
Outils mathématiques
Les vecteurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AQuelques vecteurs en physique
En physique, un vecteur peut représenter :
- un déplacement du point \text{A} au point \text{B}, noté \overrightarrow{\mathrm{AB}} : il s'agit d'un vecteur reliant les points \text{A} et \text{B}, partant de \text{A} et de longueur \text{AB}. Sa norme s'exprime en mètre (m) ;
- une vitesse en un point \text{M}, notée \overrightarrow{v} : ce vecteur est tangent à la trajectoire et est orienté dans le sens du mouvement. Sa norme est en (m·s‑1) ;
- une accélération en un point \text{M}, notée \overrightarrow{a} : le vecteur accélération décrit la variation du vecteur vitesse au cours du temps. Sa norme s'exprime en (m·s-2) ;
- une force, notée généralement \overrightarrow{F} : le vecteur associé est dirigé et orienté selon la nature de l'action mécanique. Sa norme est exprimée en newton (N).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCaractéristiques d'un vecteur
Les vecteurs possèdent trois caractéristiques :
Un vecteur peut être associé éventuellement à un point depuis lequel part le vecteur et qui désigne la position où la grandeur est représentée.
On représente usuellement les coordonnées d'un vecteur dans un repère :
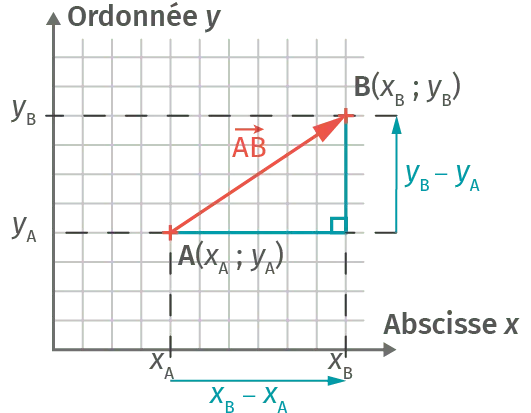
\overrightarrow{\mathrm{AB}}\left(\begin{array}{l}{x_{\mathrm{AB}}} \\ {y_{\mathrm{AB}}}\end{array}\right)=\overrightarrow{\mathrm{AB}}\left(\begin{array}{l}{x_{\mathrm{B}}-x_{\mathrm{A}}} \\ {y_{\mathrm{B}}-y_{\mathrm{A}}}\end{array}\right)
La norme du vecteur \overrightarrow{\text{AB}}, notée \text{AB} ou ||\text{AB}|| est égale à \mathrm{AB}=\sqrt{x_{\mathrm{AB}}^{2}+y_{\mathrm{AB}}^{2}} soit \text{AB} = \sqrt{(x_\text{B} - x_\text{A})^2 + (y_\text{B} - y_\text{A})^2}
- une direction correspondant à la droite sur laquelle le vecteur est représenté ;
- une norme correspondant à l'intensité ou à la valeur de la grandeur représentée, associée à une unité propre à la grandeur ;
- un sens décrivant l'orientation du vecteur.
Un vecteur peut être associé éventuellement à un point depuis lequel part le vecteur et qui désigne la position où la grandeur est représentée.
On représente usuellement les coordonnées d'un vecteur dans un repère :
\overrightarrow{\mathrm{AB}}\left(\begin{array}{l}{x_{\mathrm{AB}}} \\ {y_{\mathrm{AB}}}\end{array}\right)=\overrightarrow{\mathrm{AB}}\left(\begin{array}{l}{x_{\mathrm{B}}-x_{\mathrm{A}}} \\ {y_{\mathrm{B}}-y_{\mathrm{A}}}\end{array}\right)
La norme du vecteur \overrightarrow{\text{AB}}, notée \text{AB} ou ||\text{AB}|| est égale à \mathrm{AB}=\sqrt{x_{\mathrm{AB}}^{2}+y_{\mathrm{AB}}^{2}} soit \text{AB} = \sqrt{(x_\text{B} - x_\text{A})^2 + (y_\text{B} - y_\text{A})^2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CTracé de vecteurs
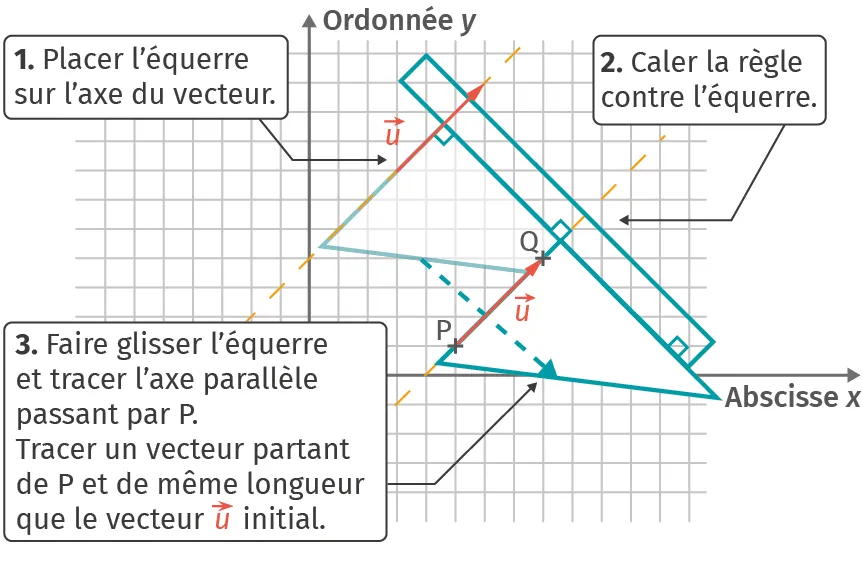
Translater un vecteur \overrightarrow{u} sur un point \text{P}.

Tracer \overrightarrow{u} + \overrightarrow{v}ou \overrightarrow{u} - \overrightarrow{v} en partant du point \text{P}.

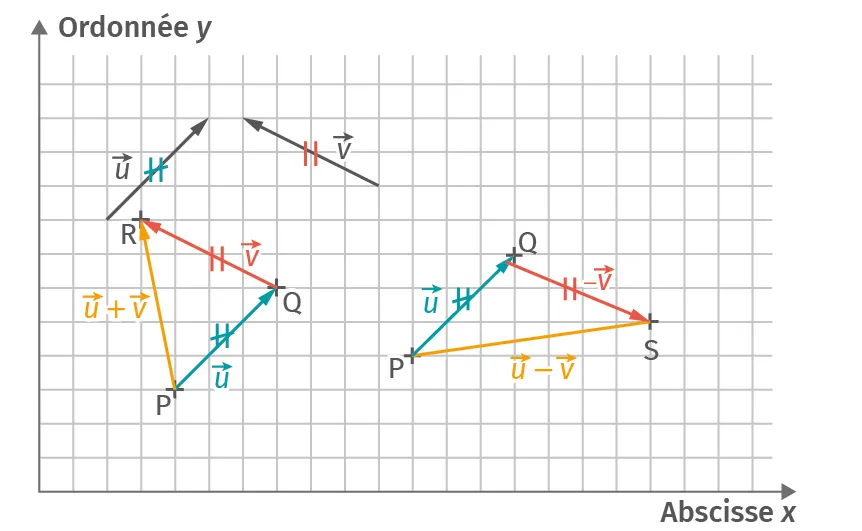
Pour avancer de -\overrightarrow{u}, on peut reprendre ces étapes et tracer le vecteur dans le sens opposé à \overrightarrow{u}.


Tracer \overrightarrow{u} + \overrightarrow{v}ou \overrightarrow{u} - \overrightarrow{v} en partant du point \text{P}.


Pour avancer de -\overrightarrow{u}, on peut reprendre ces étapes et tracer le vecteur dans le sens opposé à \overrightarrow{u}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

