1. Modéliser la dépendance entre deux grandeurs à l'aide d'une fonction.
2. Résoudre graphiquement une équation du type f(x) = k ou une inéquation du type f(x)>k, où k est un réel.
3. Déterminer les éléments caractéristiques de certaines fonctions polynômes du second degré.
4. Factoriser une expression du second degré dans des cas simples.
5. Résoudre des équations de la forme x^2 = c ou x^3 = c, où c est un réel positif.

Développer une expression : transformer un produit en somme

Soient k, a, b, c et d des nombres quelconques. On a les propriétés suivantes :
1. Distributivité simple : k(a+b) = ka+kb
2. Double distributivité : (a+b)(c+d) = ac+ad+bc+bd
3. Identité remarquable : (a+b)(a-b) = a^2-b^2

Factoriser une expression : transformer une somme en produit

• Distributivité avec un facteur commun :
  ka + kb = k(a+b) ou ka - kb = k(a-b).
• Identités remarquables :
  \begin{aligned} a^2 -b^2 &= (a+b)(a-b) \\ a^2 + 2ab + b^2 &= (a+b)^2 \\ a^2 - 2ab +b^2 &= (a-b)^2 \end{aligned}

Méthode :

Pour étudier le signe d'un produit de facteurs, on étudie le signe de chacun des facteurs en résolvant des inéquations, et on regroupe les résultats dans un tableau de signes.

Exemple :

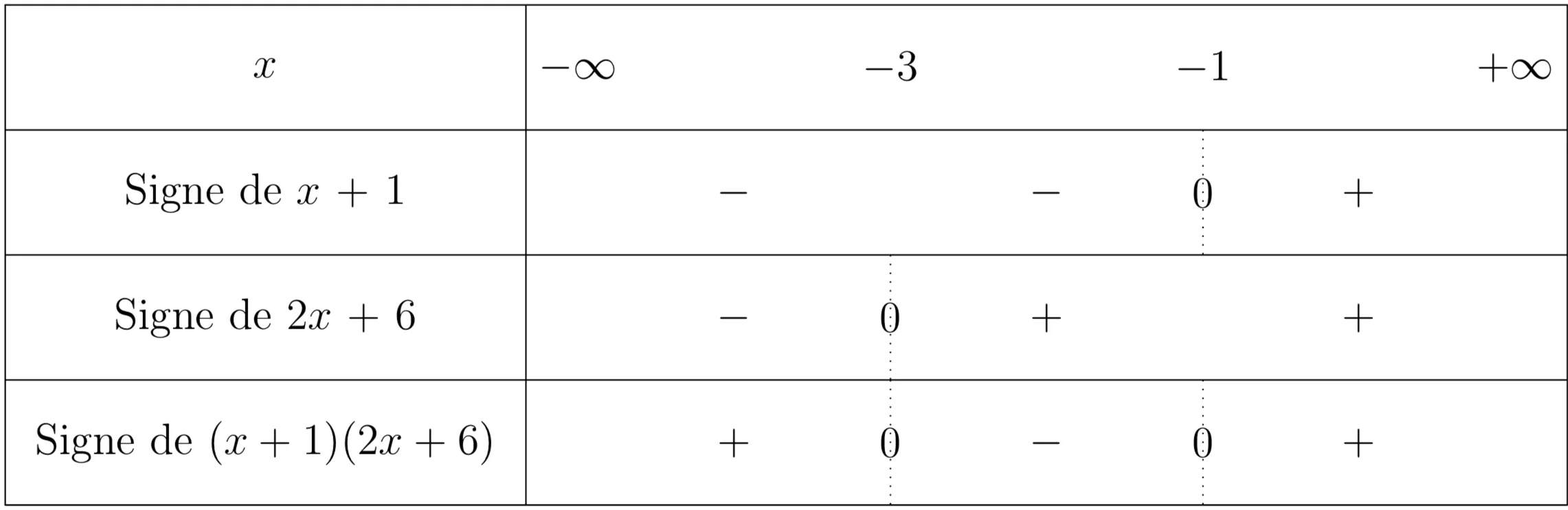
On veut étudier le signe de (x+1)(2x +6) pour x un nombre réel.
On résout les inéquations
x+ 1 \leqslant 0 \Leftrightarrow x \leqslant -1 et 2x + 6 \leqslant 0 \Leftrightarrow 2x \leqslant -6 \Leftrightarrow x \leqslant \dfrac{-6}{2} = -3.
Enfin, on dresse le tableau de signe donnant le signe de chacun des facteurs en fonction de la valeur de x, et on déduit le signe du produit en utilisant la règle des signes :

Définition :

a, b, c et d désignent quatre nombres connus et x désigne l'inconnue.
1. Une équation du premier degré à une inconnue est une égalité pouvant s'écrire sous la forme ax + b = cx + d.
Résoudre une équation c'est trouver, si elles existent, toutes les valeurs de l'inconnue pour lesquelles l'égalité est vérifiée.
2. Une inéquation du premier degré à une inconnue est une inégalité du type ax + b \leqslant cx+d ou ax+b \geqslant cx+d.
Résoudre une inéquation, c'est trouver toutes les valeurs de l'inconnue pour lesquelles l'inégalité est vérifiée.

Propriétés :

1. Une égalité reste vraie lorsqu'on ajoute (ou soustrait) un même nombre à ses deux membres.
2. Une égalité reste vraie lorsqu'on multiplie (ou divise) ses deux membres par un même nombre.

Méthode :

Pour résoudre une équation de la forme ax + b = cx+d, on cherche à isoler x : on retire b des deux côtés, puis on retire cx, et on divise par le coefficient restant devant x.

Exemple :

\begin{aligned} 3x+2 = 6x+1 &\Leftrightarrow 3x = 6x + 1 - 2 = 6x-1 \\ &\Leftrightarrow 3x - 6x = 6x-1-6x \\ &\Leftrightarrow -3x = -1 \\ &\Leftrightarrow x = \dfrac{1}{3} \end{aligned}

Propriétés :

1. Une inégalité reste vraie lorsqu'on ajoute (ou soustrait) un même nombre à ses deux membres.
2. Une inégalité reste vraie lorsqu'on multiplie (ou divise) ses deux membres par un même nombre strictement positif.
3. Une inégalité change de sens lorsqu'on multiplie (ou divise) ses deux membres par un même nombre strictement négatif.

Définition :

Il y a 3 principaux modes de définition d'une fonction f permettant d'associer à un réel x de l'ensemble de définition \text{D}, son image y :
1. Avec une relation algébrique : on connaît directement l'expression de f\left(x\right) en fonction de x. Par exemple, la fonction f définie sur \mathbb{R} par : f\left(x\right)= x^{2} + x + 1. Cela permet le calcul exact de l'image y de toute valeur de x de l'ensemble de définition. Il suffit de remplacer x par le nombre souhaité dans l'expression.

2. Avec un tableau de valeurs : on donne explicitement les images associées à différentes valeurs de x. Par exemple, ici, g\left(-1\right) = 0 et 2 admet pour antécédents 0 et 10.


Ce mode de définition ne permet de connaître qu'un nombre fini d'images.

3. Avec une courbe : la courbe représentative d'une fonction h est l'ensemble des points \mathrm{A}\left( x~; y \right) tels que y = h\left(x\right).
Elle donne les valeurs de la fonction sur tout l'ensemble de définition, mais la précision est limitée par la lecture graphique.

Fonction carré

Définition :

La fonction carré est la fonction qui, à tout réel x, associe le réel x^2.
Sa courbe représentative est une parabole.

Propriétés :

1. Pour tout réel x, x^2\geqslant 0.
2. La fonction carré est paire.
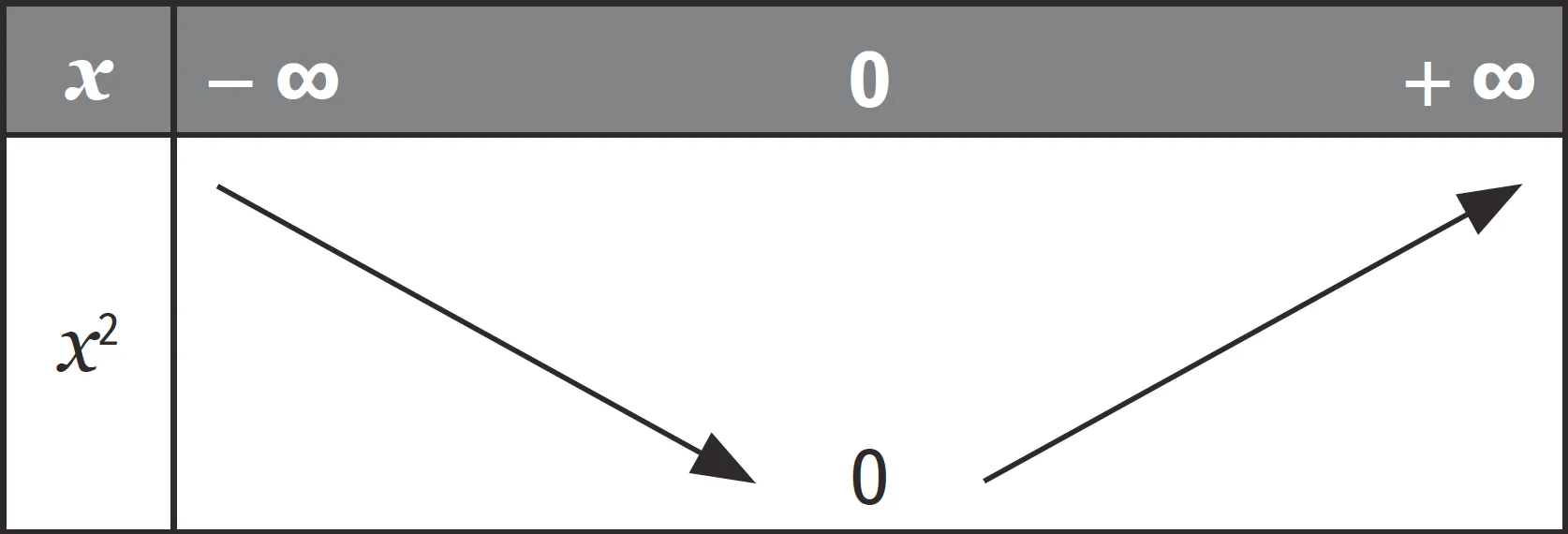
3. La fonction carré est strictement décroissante sur \left]-\infty~;0\right] et strictement croissante sur \left[0~;+\infty\right[.
4. Une équation du type x^2 = a possède deux solutions \sqrt a et -\sqrt a si a > 0, une seule solution 0 si a=0, et aucune solution si a \lt 0.

Fonction cube

Définition :

La fonction cube est la fonction qui, à tout réel x, associe le réel x^3.

Propriétés :

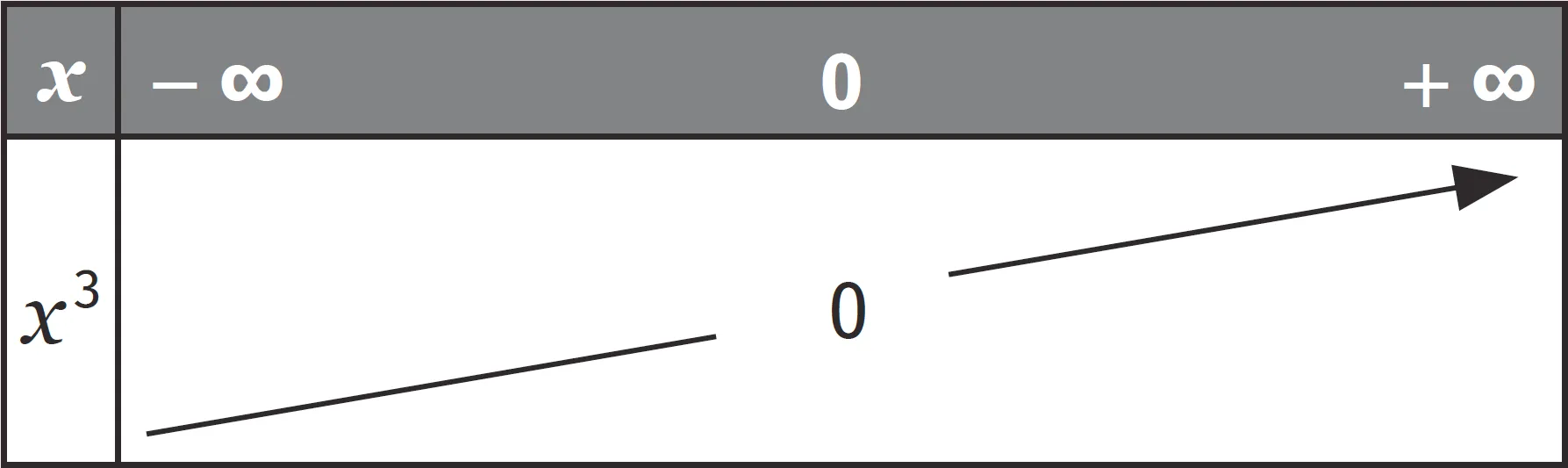
La fonction cube :
1. est impaire ;
2. est strictement croissante sur \mathbb{R}.

1. Manipuler les expressions algébriques.
2. Résoudre une équation ou une inéquation du premier degré.
3. Construire et exploiter le tableau de signe d'un produit de facteurs du premier degré.
4. Utiliser les différents modes de représentation d'une fonction.
5. Connaître les fonctions de référence, notamment les fonctions carré et cube.

Construire sur \mathbb{R} le tableau de signe des expressions suivantes.

1. (x-4)(x-7)

2. (2 x+6)(3 x-9)

3. (2 x-4)(4 x-12)(x+5)

On considère une fonction g dont la représentation graphique C_g est donnée ci‑dessous.



1. Déterminer graphiquement les images de -1, 0 et 3 par cette fonction g.

2. On considère la fonction f : x \mapsto 2(x + 1) (x - 3).
a. Résoudre l'équation f(x) = 0.

b. Calculer f(0). La courbe ci‑dessus peut‑elle être la courbe représentative de f ? Pourquoi ?