Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 2
TP Info
Recherche d'une solution par balayage
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Une entreprise produit des granulés de bois. Les bénéfices de cette entreprise sont modélisés par la fonction \text{B} définie, pour tout x \in [0~;25], par \mathrm{B}(x)=-x^{3}+20 x^{2}+20 x-450, où x désigne la quantité de granulés vendue, en tonne, et \mathrm{B}(x) les bénéfices correspondants, en euro. L'entreprise souhaite déterminer, à la centaine de kilogrammes près, pour quelles productions elle peut faire des bénéfices.
Pour ce faire, elle souhaite utiliser un algorithme de balayage.
Le principe est le suivant : on évalue les bénéfices pour une certaine valeur de \bm{x}, puis on regarde la valeur des bénéfices à \bm{x+p}, où \bm{p} est un réel fixé que l'on appelle le pas. On continue tant que les bénéfices ne changent pas de signe.
Pour ce faire, elle souhaite utiliser un algorithme de balayage.
Le principe est le suivant : on évalue les bénéfices pour une certaine valeur de \bm{x}, puis on regarde la valeur des bénéfices à \bm{x+p}, où \bm{p} est un réel fixé que l'on appelle le pas. On continue tant que les bénéfices ne changent pas de signe.
Le zoom est accessible dans la version Premium.
Questions préliminaires
1. a. Calculer les valeurs de \mathrm{B}(4), \mathrm{B}(5), \mathrm{B}(19) et \mathrm{B}(20).
b. Combien de solutions l'équation \mathrm{B}(x)=0 admet‑elle au minimum ?
2. Convertir 100 kilogrammes en tonne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Résoudre de manière approchée l'équation \boldsymbol{\mathrm{B}(x) = 0} à l'aide d'un algorithme de balayage à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode de résolution 1
Python
L'objectif est de compléter le programme ci‑contre, écrit en Python, pour répondre à la question posée.
1. Compléter la ligne 2 du programme à l'aide de l'expression algébrique de la fonction \text{B}.
2. Quel est le signe de \mathrm{B}(4) ? Compléter les lignes 6 et 7 de l'algorithme.
3. Exécuter \color{purple}\bf{balayage(0.1)}, puis interpréter le résultat obtenu dans le contexte de cet exercice.
1. Compléter la ligne 2 du programme à l'aide de l'expression algébrique de la fonction \text{B}.
2. Quel est le signe de \mathrm{B}(4) ? Compléter les lignes 6 et 7 de l'algorithme.
3. Exécuter \color{purple}\bf{balayage(0.1)}, puis interpréter le résultat obtenu dans le contexte de cet exercice.
def B(x):
return ...
def balayage(pas):
x=4
while B(x) < ... :
x = ...
return (x - pas, x)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode de résolution 2
Tableur
On dresse un tableau de valeurs avec un pas fixé dans la cellule E1.
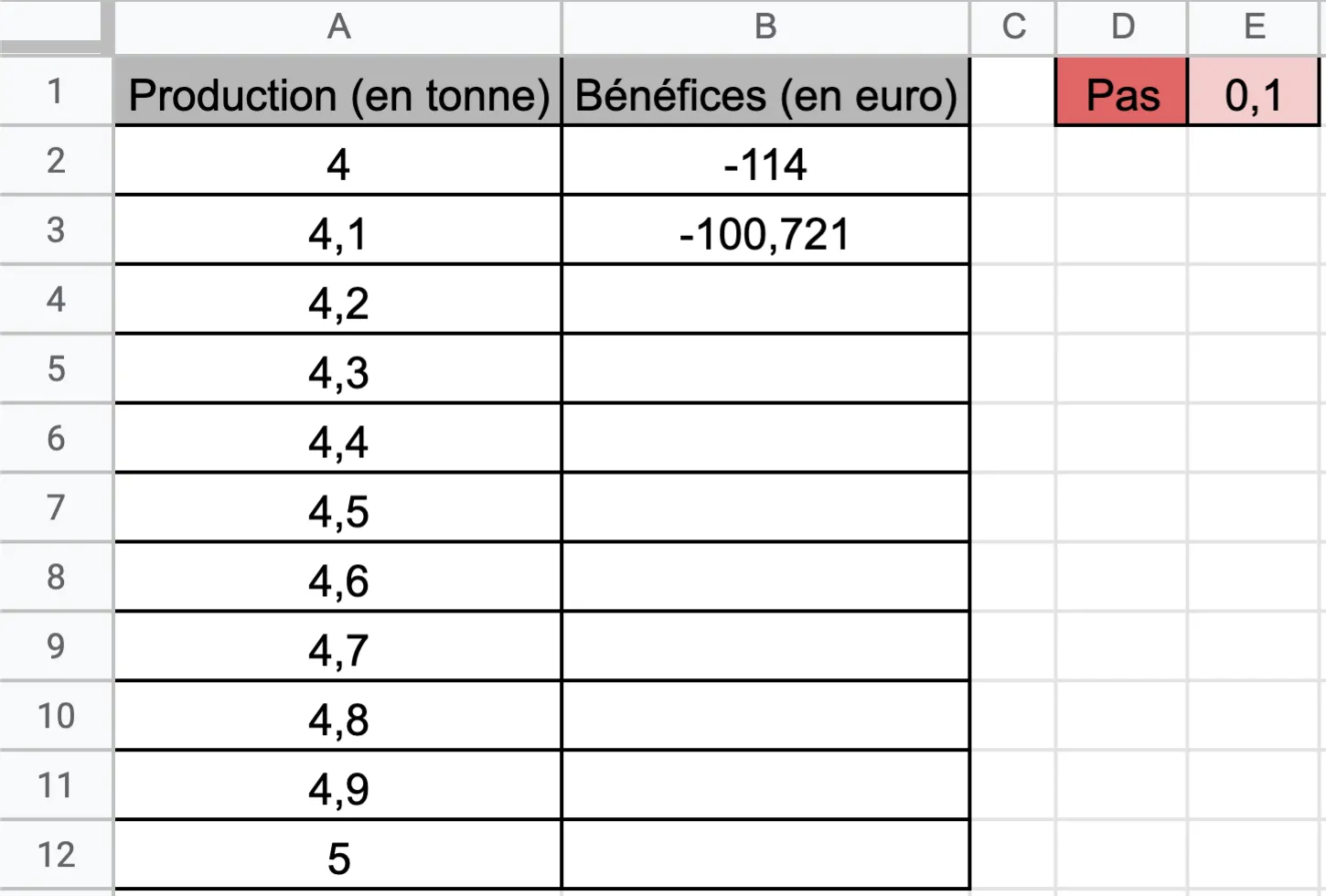
1. Quelle formule a été saisie dans la cellule A3, puis étirée vers le bas, pour obtenir les valeurs de la colonne A ?
2. Quelle formule doit‑on saisir dans la cellule B3, puis étirer vers le bas, pour calculer les bénéfices de l'entreprise ?
3. Donner un encadrement d'amplitude 10^{-1} d'une solution de l'équation \mathrm{B}(x) = 0.
4. On souhaite déterminer un encadrement d'amplitude 10^{-2} de cette solution. Modifier la feuille de calcul sur le logiciel de tableur de votre choix pour en tenir compte.
Le zoom est accessible dans la version Premium.
1. Quelle formule a été saisie dans la cellule A3, puis étirée vers le bas, pour obtenir les valeurs de la colonne A ?
2. Quelle formule doit‑on saisir dans la cellule B3, puis étirer vers le bas, pour calculer les bénéfices de l'entreprise ?
3. Donner un encadrement d'amplitude 10^{-1} d'une solution de l'équation \mathrm{B}(x) = 0.
4. On souhaite déterminer un encadrement d'amplitude 10^{-2} de cette solution. Modifier la feuille de calcul sur le logiciel de tableur de votre choix pour en tenir compte.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Les méthodes ci‑dessus permettent de déterminer la première solution de l'équation \mathrm{B}(x) = 0. En s'inspirant de ces deux méthodes, donner une valeur approchée de la deuxième solution de l'équation \mathrm{B}(x) = 0.
2. Plutôt que de chercher les valeurs pour lesquelles l'entreprise réalise des bénéfices, on souhaite chercher la production pour laquelle le bénéfice est maximal. On admet qu'il existe un réel a tel que la fonction \text{B} est croissante sur [10~; a] et décroissante sur [a~; 15]. Déterminer une valeur approchée à 10^{-2} près de a à l'aide d'un algorithme de balayage.
3. Interpréter alors les résultats de ces deux questions dans le contexte de l'exercice.
2. Plutôt que de chercher les valeurs pour lesquelles l'entreprise réalise des bénéfices, on souhaite chercher la production pour laquelle le bénéfice est maximal. On admet qu'il existe un réel a tel que la fonction \text{B} est croissante sur [10~; a] et décroissante sur [a~; 15]. Déterminer une valeur approchée à 10^{-2} près de a à l'aide d'un algorithme de balayage.
3. Interpréter alors les résultats de ces deux questions dans le contexte de l'exercice.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah