Mathématiques 1re Techno
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Analyse
Ch. 1
Suites
Ch. 2
Fonctions
Ch. 3
Dérivation
Partie 2 : Statistiques et probabilités
Ch. 4
Fréquences conditionnelles et probabilités conditionnelles
Ch. 5
Variables aléatoires
Automatismes
Partie 3 : Géométrie
Ch. 6
Trigonométrie
Ch. 7
Produit scalaire
Ch. 8
Nombres complexes
Partie 4 : Analyse
Ch. 9
Compléments sur la dérivation
Ch. 10
Primitives
Révisions Genially
Chapitre 2
Exercices
Synthèse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 83 [Représenter, Modéliser.]
Une entreprise fabrique des objets qu'elle vend ensuite au prix de 12 € l'unité. Pour x objets vendus, le chiffre d'affaires de cette entreprise s'élève donc à g(x)=12 x~€.
Par ailleurs, le coût de fabrication de x objets s'élève à f(x)~€, où f est une fonction définie sur [0~; 50].
Les représentations graphiques des fonctions f et g sont données ci‑dessous dans un repère orthogonal.

Partie A : Lecture graphique
1. Par lecture graphique, déterminer le coût de fabrication de 10 objets.
2. Déterminer graphiquement les abscisses des points d'intersection des courbes représentatives de f et de g.
3. Interpréter la réponse donnée à la question précédente dans le contexte de l'exercice.
Partie B : Étude algébrique
On admet que pour toutx \in[0~; 50] :
4. Montrer que, pour tout x \in[0~; 50], le bénéfice \mathrm{B}(x) de l'entreprise vaut \mathrm{B}(x)=g(x)-f(x)=-x^{2}+52 x-480.
5. a. Montrer que pour tout x \in[0~; 50] :
b. Construire le tableau de signe de \text{B}. En déduire les valeurs de x pour lesquelles l'entreprise réalise un bénéfice.
6. a. Dresser le tableau de variations de la fonction \text{B} sur [0~; 50]. On pensera à faire apparaître les valeurs de \mathrm{B}(0) et de \mathrm{B}(50).
b. Pour quelle production d'objets le bénéfice de l'entreprise est‑il maximal ? Que vaut alors ce bénéfice ?
Par ailleurs, le coût de fabrication de x objets s'élève à f(x)~€, où f est une fonction définie sur [0~; 50].
Les représentations graphiques des fonctions f et g sont données ci‑dessous dans un repère orthogonal.

Partie A : Lecture graphique
1. Par lecture graphique, déterminer le coût de fabrication de 10 objets.
2. Déterminer graphiquement les abscisses des points d'intersection des courbes représentatives de f et de g.
3. Interpréter la réponse donnée à la question précédente dans le contexte de l'exercice.
Partie B : Étude algébrique
On admet que pour toutx \in[0~; 50] :
f(x)=x^{2}-40 x+480.
4. Montrer que, pour tout x \in[0~; 50], le bénéfice \mathrm{B}(x) de l'entreprise vaut \mathrm{B}(x)=g(x)-f(x)=-x^{2}+52 x-480.
5. a. Montrer que pour tout x \in[0~; 50] :
\mathrm{B}(x)=-(x-40)(x-12).
b. Construire le tableau de signe de \text{B}. En déduire les valeurs de x pour lesquelles l'entreprise réalise un bénéfice.
Cliquez pour accéder à une zone de dessin
6. a. Dresser le tableau de variations de la fonction \text{B} sur [0~; 50]. On pensera à faire apparaître les valeurs de \mathrm{B}(0) et de \mathrm{B}(50).
Cliquez pour accéder à une zone de dessin
b. Pour quelle production d'objets le bénéfice de l'entreprise est‑il maximal ? Que vaut alors ce bénéfice ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 84 [Calculer, Modéliser.]


L'échelle de Beaufort est une échelle de mesure empirique de la vitesse du vent.
Pour des vents ayant une vitesse en‑deçà de 118 km/h, le degré de Beaufort \text{B} et la vitesse du vent v en km/h sont reliés par la relation :
\mathrm{B}^{3}=\frac{v^{2}}{9}.
Le nombre \text{B} est en général arrondi à l'entier le plus proche.
1. À quel degré de Beaufort (ou force) est associé un vent qui souffle à 100 km/h ?
2. À quelle vitesse souffle une tempête de force 9 sur l'échelle de Beaufort ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 85[Représenter, Communiquer.]
Un objet est lâché depuis un pont qui se situe au dessus d'une rivière. La hauteur de l'objet par rapport à la rivière en fonction du temps est représentée ci‑dessous.

1. À quelle hauteur se situe le pont par rapport à la rivière ?
2. Donner une approximation graphique du temps auquel l'objet touche l'eau.
3. On peut démontrer, grâce aux lois de Newton, qu'au temps t, la hauteur de l'objet vaut h(t)=-\frac{1}{2} g t^{2}+30, où g=9,8 \mathrm{~m} / \mathrm{s}^{2} désigne l'accélération de la pesanteur.
Répondre avec plus de précision aux questions 1. et 2. en exploitant l'expression algébrique de h.

1. À quelle hauteur se situe le pont par rapport à la rivière ?
2. Donner une approximation graphique du temps auquel l'objet touche l'eau.
3. On peut démontrer, grâce aux lois de Newton, qu'au temps t, la hauteur de l'objet vaut h(t)=-\frac{1}{2} g t^{2}+30, où g=9,8 \mathrm{~m} / \mathrm{s}^{2} désigne l'accélération de la pesanteur.
Répondre avec plus de précision aux questions 1. et 2. en exploitant l'expression algébrique de h.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 86 [Modéliser, Communiquer.]
D'après bac ST2S, Métropole, 2013
Pour traiter un patient, un médecin procède à l'injection intramusculaire d'une dose d'une substance médicamenteuse au temps t = 0, t étant exprimé en heure.
Le produit actif se diffuse dans le sang puis est progressivement éliminé. Le médicament est efficace lorsque la concentration du produit actif dans le sang est supérieure ou égale à 25 mg/L (25 milligrammes par litre).
La concentration maximale du produit actif dans le sang ne peut pas dépasser 40 mg/L pour éviter des effets secondaires.
Partie A : Étude graphique
La courbe donnée ci‑dessous représente la concentration en mg/L du produit actif dans le sang du malade en fonction du temps écoulé depuis l'injection du médicament.

À l'aide de cette courbe, répondre, avec la précision qu permet le graphique, aux questions suivantes.
1. Déterminer la concentration du produit actif pour t = 5 \text{ h}.
2. Le médecin a‑t‑il respecté la dose à ne pas dépasser ? Expliquer.
3. Déterminer les temps, en heure et en minute, auxquels la concentration du produit actif est de 15 mg/L.
4. Quelle est la durée pendant laquelle le médicament est resté efficace ?
5. Au bout de quelle durée le médicament est‑il complètement éliminé ?
Partie B : Étude numérique
On admet que la concentration, exprimée en mg/L, du produit actif dans le sang du malade est donnée en fonction du temps t, exprimé en heure, par la fonction f définie sur l'intervalle [0~; 6] par : f(t)=t^{3}-12 t^{2}+36 t.
6. Montrer que, pour tout t dans [0~; 6], f(t)=t(t-6)^{2}.
7. En déduire les solutions de l'équation f(t) = 0 et interpréter ces solutions dans le cadre de l'exercice.
Pour traiter un patient, un médecin procède à l'injection intramusculaire d'une dose d'une substance médicamenteuse au temps t = 0, t étant exprimé en heure.
Le produit actif se diffuse dans le sang puis est progressivement éliminé. Le médicament est efficace lorsque la concentration du produit actif dans le sang est supérieure ou égale à 25 mg/L (25 milligrammes par litre).
La concentration maximale du produit actif dans le sang ne peut pas dépasser 40 mg/L pour éviter des effets secondaires.
Partie A : Étude graphique
La courbe donnée ci‑dessous représente la concentration en mg/L du produit actif dans le sang du malade en fonction du temps écoulé depuis l'injection du médicament.

À l'aide de cette courbe, répondre, avec la précision qu permet le graphique, aux questions suivantes.
1. Déterminer la concentration du produit actif pour t = 5 \text{ h}.
2. Le médecin a‑t‑il respecté la dose à ne pas dépasser ? Expliquer.
3. Déterminer les temps, en heure et en minute, auxquels la concentration du produit actif est de 15 mg/L.
4. Quelle est la durée pendant laquelle le médicament est resté efficace ?
5. Au bout de quelle durée le médicament est‑il complètement éliminé ?
Partie B : Étude numérique
On admet que la concentration, exprimée en mg/L, du produit actif dans le sang du malade est donnée en fonction du temps t, exprimé en heure, par la fonction f définie sur l'intervalle [0~; 6] par : f(t)=t^{3}-12 t^{2}+36 t.
6. Montrer que, pour tout t dans [0~; 6], f(t)=t(t-6)^{2}.
7. En déduire les solutions de l'équation f(t) = 0 et interpréter ces solutions dans le cadre de l'exercice.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le concept de fonction a été introduit au XVIIe siècle par Gottfried Wilhem Leibniz (1646 - 1716). Il s'agissait alors d'assigner une valeur à un point d'une courbe. La notion d'expression algébrique d'une fonction ne vint que bien des années plus tard, sous l'impulsion notamment de Leonhard Euler (1707-1783).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 87 [Calculer, Représenter.]


Un joueur renvoie une balle de tennis. La hauteur de la balle en fonction de la distance à ce joueur est modélisée par une fonction f dont la courbe représentative est donnée ci‑dessous.

1. Déterminer graphiquement :
a. la distance parcourue horizontalement lorsque la balle touche le sol.
b. la distance parcourue horizontalement lorsque la balle atteint sa hauteur maximale.
2. On admet que cette courbe est la courbe représentative de la fonction f définie sur [0~; 11] :
f(x)=-0{,}05 x^{2}+0{,}4 x+1{,}65.
a. Calculer f(11). Que retrouve‑t‑on ?
b. Montrer que -3 est une racine de f.
c. En déduire une forme factorisée de f.
d. Retrouver par le calcul l'équation de l'axe de symétrie de la courbe représentative de f.
e. En utilisant la symétrie de la courbe représentative de f, résoudre l'équation f(x)=1{,}65.
Interpréter ce résultat dans le contexte de l'exercice.
3. Pour tout réel x \in[0~; 11], on pose :
g(x)=f(x)-1{,}65.
a. Montrer que pour tout x \in[0~; 11] :
g(x)=-x(0{,}05 x-0{,}4).
b. Résoudre l'équation g(x)=0 sur [0~; 11].
c. En déduire la distance parcourue horizontalement lorsque la balle repasse sous la barre des 1,65 m de hauteur.
Aide
On pourra étudier le signe de g sur [0~; 11].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 88[Calculer, Raisonner.]
On s'intéresse à une méthode de multiplication utilisant la parabole représentative de la fonction f: x \mapsto x^{2} dans un repère (0~;\overrightarrow{i}~,\overrightarrow{j}).
Pour deux réels positifs a et b, il est possible de lire le produit ab comme suit :
Ci‑dessous se trouve une illustration de ce procédé pour calculer le produit 2 \times 5.

1. a. Écrire l'équation de la droite passant par les points de coordonnées (2~; 4) et (-5~; 25).
b. Vérifier que cette droite passe bien par le point de coordonnées (0~; 10).
2. Cas général
Pour a et b deux réels positifs, vérifier que la droite passant par les points de coordonnées \left(a~; a^{2}\right) et \left(-b~; b^{2}\right) passe également par le point de coordonnées (0~; a b).
Pour deux réels positifs a et b, il est possible de lire le produit ab comme suit :
- on place les points \text{A} et \text{B} d'abscisses a et -b sur la courbe de f ;
- on trace la droite (\mathrm{AB}) ;
- le produit ab se lit sur l'intersection de cette droite avec l'axe des ordonnées.
Ci‑dessous se trouve une illustration de ce procédé pour calculer le produit 2 \times 5.

1. a. Écrire l'équation de la droite passant par les points de coordonnées (2~; 4) et (-5~; 25).
b. Vérifier que cette droite passe bien par le point de coordonnées (0~; 10).
2. Cas général
Pour a et b deux réels positifs, vérifier que la droite passant par les points de coordonnées \left(a~; a^{2}\right) et \left(-b~; b^{2}\right) passe également par le point de coordonnées (0~; a b).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 89 [Calculer, Modéliser.]


Une entreprise fabrique quotidiennement entre 0 et 25 pièces pour l'industrie automobile. Le montant des charges pour x pièces fabriquées, en euro, est modélisé par la fonction \text{C} définie sur [0~; 25] par :
\mathrm{C}(x)=x^{3}-30 x^{2}+400 x+100.
1. Quel est le montant des charges pour cinq pièces produites par jour ?
2. Chaque pièce est vendue 247 €. On suppose que l'entreprise vend chaque jour sa production journalière.
a. On note \text{B} la fonction bénéfice, exprimée en euro.
Justifier que, pour tout x \in[0~; 25], on a :
\mathrm{B}(x)=-x^{3}+30 x^{2}-153 x-100.
b. On donne les variations de la fonction \text{B}.

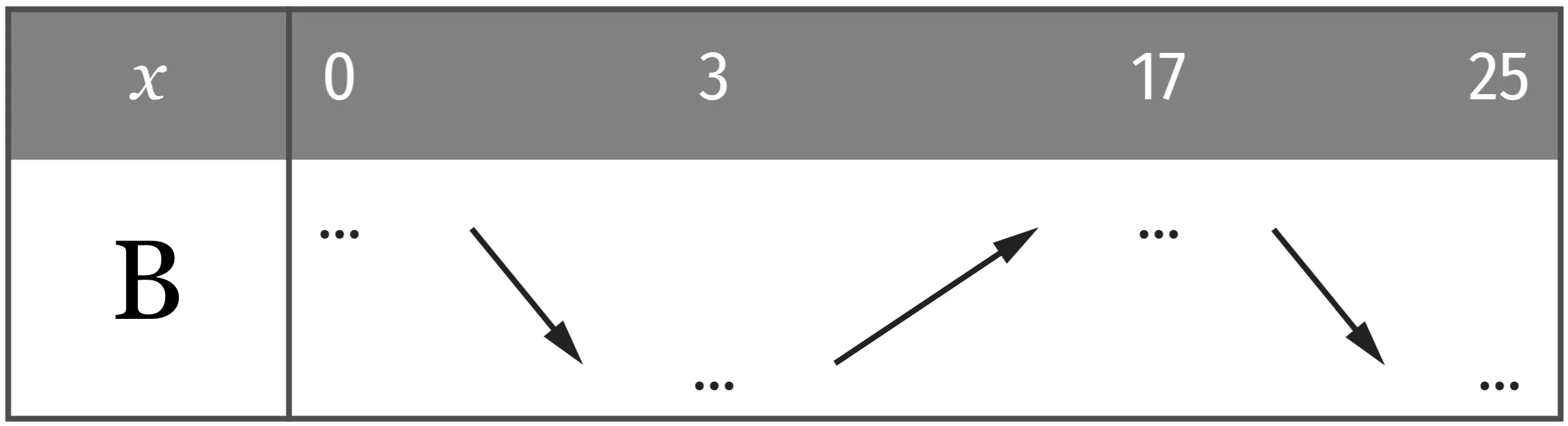
Compléter ce tableau, puis déterminer le nombre de pièces que l'entreprise doit produire pour que son bénéfice soit maximal. Que vaut alors ce bénéfice ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 90Énigme
Le cube d'un nombre est‑il toujours plus grand que son carré ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 91 Défi


Le viaduc de Gabarit, construit de 1880 à 1884, possédait alors l'arche ayant la plus grande portée du monde.
La distance entre la base des deux piliers principaux est de 165 mètres. Chaque pilier a une hauteur de 58 mètres.
On construit un repère orthonormé en plaçant l'origine à la base du premier pilier. Donner une équation de l'arche parabolique de ce viaduc.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
