D'après le théorème de la médiane on a : \overrightarrow{\mathrm{MA}} \cdot \overrightarrow{\mathrm{MB}}=\mathrm{MI}^{2}-\dfrac{1}{4} \mathrm{AB}^{2}.
Donc \overrightarrow{\mathrm{MA}} \cdot \overrightarrow{\mathrm{MB}}=k {\Leftrightarrow \mathrm{MI}^{2}-\dfrac{1}{4} \mathrm{AB}^{2}=k} {\Leftrightarrow \mathrm{MI}^{2}=k+\dfrac{1}{4} \mathrm{AB}^{2}}.

• Si k+\dfrac{1}{4} \mathrm{AB}^{2}\lt0 alors il n'y a pas de solution : \mathcal{S}=\emptyset.
• Si k+\dfrac{1}{4} \mathrm{AB}^{2} = 0 alors seul le point \text{I} vérifie \mathrm{MI}^{2}=0 : \mathcal{S}=\{\mathrm{I}\}.
• Si k+\dfrac{1}{4} \mathrm{AB}^{2}\gt0 alors \mathcal{S} est le cercle de centre \text{I} et de rayon \sqrt{k+\dfrac{1}{4} \mathrm{AB}^{2}}.

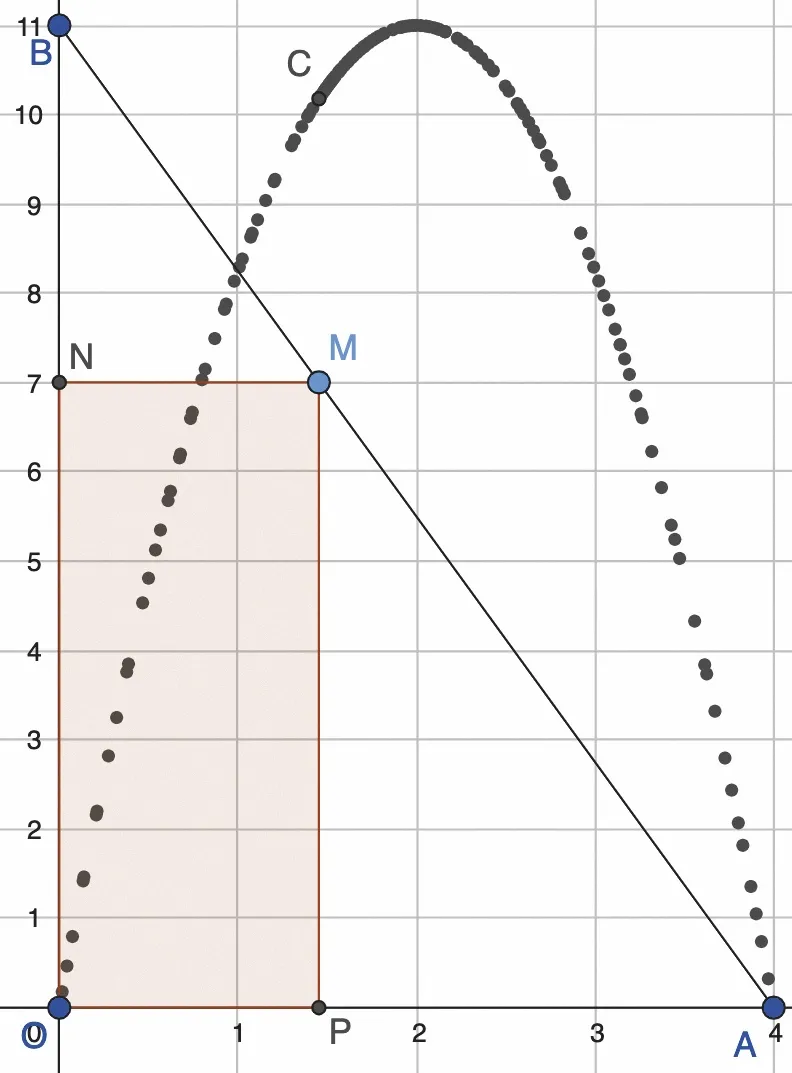
Soient les points \text{A}(4\: ; 0) et \text{B}(0\: ; 11). On place un point \text{M} sur le segment \text{[AB]} et on place \text{N} et \text{P} sur les axes de façon à ce que \text{MNOP} soit un rectangle.
On veut savoir où placer le point \text{M} de façon à ce que l'aire du rectangle soit maximale.
Dans GeoGebra, on a tracé la figure et on a fait afficher un point \text{C} qui a pour abscisse celle du point \text{M} et pour ordonnée l'aire du rectangle.
Le point qui maximise cette aire est donc le point de coordonnées (2 \:; 5{,}5).