Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 10
TP / TICE 1
Déterminer un lieu géométrique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On pose une échelle qui mesure 3 m contre un mur. Le pied de l'échelle glisse contre le sol. On assimile l'échelle à un segment \text{[AB]} : on note \text{A} le pied de l'échelle, \text{B} son sommet et \text{I} le milieu de \text{[AB].} \text{I} est donc le centre de l'échelle. On note x la distance en mètre mesurée au sol entre le pied de l'échelle et le mur.
Énoncé
Questions préliminaires :
1. Quelles valeurs peut prendre x ?
2. Déterminer, en fonction de x, la hauteur mesurée sur le mur du haut de l'échelle par rapport au sol.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Déterminer le lieu géométrique décrit par le centre de l'échelle lorsqu'elle glisse contre le mur en utilisant une des trois méthodes.
Objectif
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. Construction de la figure :
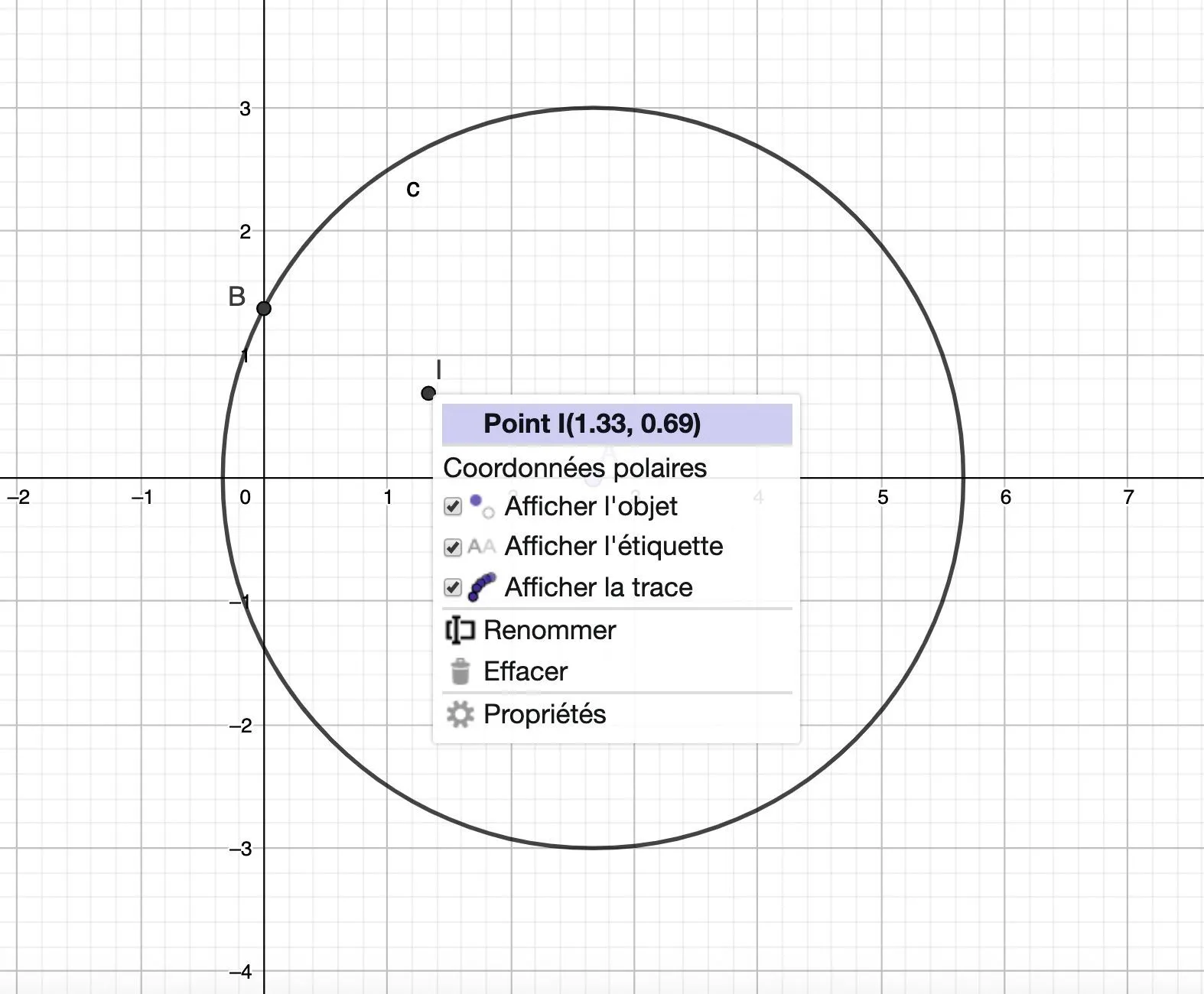
a. Placer le point \text{A} sur l'axe des abscisses.
b. Tracer un cercle de centre \text{A} et de rayon 3 : on place le point \text{B} d'ordonnée positive à l'intersection du cercle avec l'axe des ordonnées.
c. Placer le milieu \text{I} de \text{[AB].}
d. Après avoir activé l'option Afficher la trace dans le menu d'option du point \text{I} (clic droit), faire bouger le point \text{A} sur l'axe des abscisses.

a. Placer le point \text{A} sur l'axe des abscisses.
b. Tracer un cercle de centre \text{A} et de rayon 3 : on place le point \text{B} d'ordonnée positive à l'intersection du cercle avec l'axe des ordonnées.
c. Placer le milieu \text{I} de \text{[AB].}
d. Après avoir activé l'option Afficher la trace dans le menu d'option du point \text{I} (clic droit), faire bouger le point \text{A} sur l'axe des abscisses.


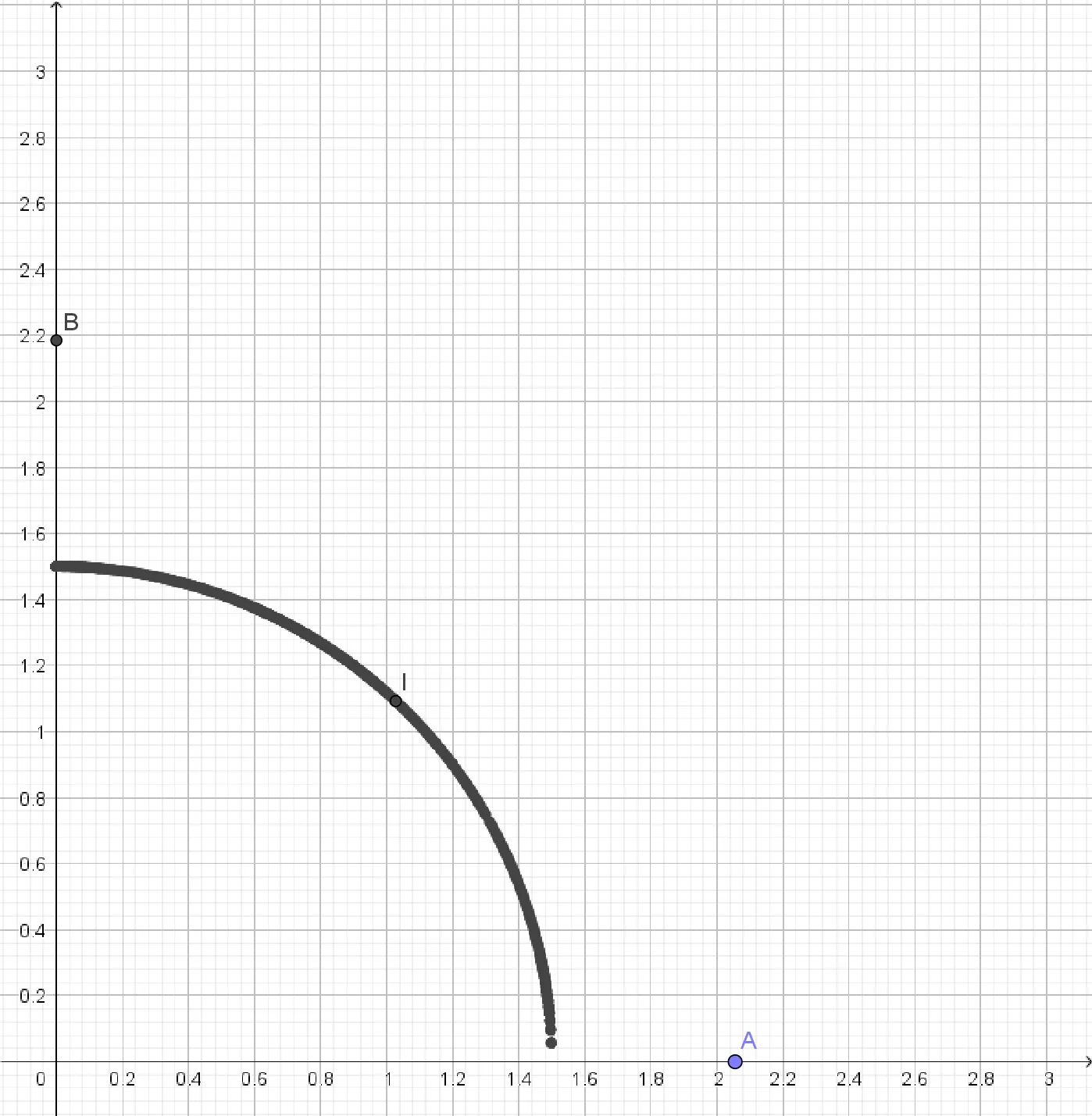
2. Conjecturer alors le lieu parcouru par le point \text{I.}
Cliquez pour accéder à une correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
On se place dans un repère orthonormé (\text{O} ; \vec{i} , \vec{j} ) où l'axe des abscisses modélise le sol et l'axe des ordonnées modélise le mur. Dans ce repère, x correspond donc à l'abscisse de \text{A} et la hauteur du sommet \text{B} de l'échelle est l'ordonnée du point \text{B.}
1. a. Ouvrir une feuille de calcul et la compléter en suivant les instructions ci-après.




Cliquez pour accéder à une correction


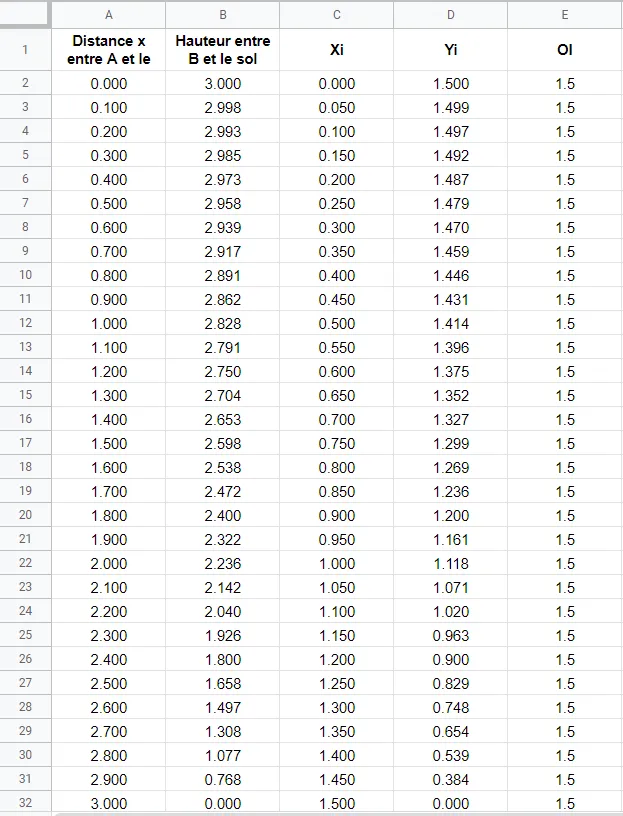
b. Dans la première colonne, rentrer les valeurs possibles de x avec un pas de 0{,}1.
c. Dans la deuxième colonne, calculer l'ordonnée du point \text{B.}
d. Dans les troisièmes et quatrièmes colonnes, calculer les coordonnées du point \text{I.}
e. Dans la cinquième colonne, calculer la longueur \text{OI.}
2. Conjecturer le lieu parcouru par le point \text{I.}
c. Dans la deuxième colonne, calculer l'ordonnée du point \text{B.}
d. Dans les troisièmes et quatrièmes colonnes, calculer les coordonnées du point \text{I.}
e. Dans la cinquième colonne, calculer la longueur \text{OI.}
2. Conjecturer le lieu parcouru par le point \text{I.}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 3Python
On se place dans un repère orthonormé (\text{O} ; \vec{i} , \vec{j} ) où l'axe des abscisses modélise le sol et l'axe des ordonnées modélise le mur. Dans ce repère, x correspond donc à l'abscisse de \text{A} et la hauteur du sommet \text{B} de l'échelle est l'ordonnée du point \text{B.}
1. Créer deux fonctions avec Python qui permettent de calculer respectivement chaque coordonnée de \text{I} en fonction de x .
2. Élaborer un programme écrit avec Python qui permet de calculer la longueur \text{OI} lorsque x varie entre 0 et 3 avec un pas de 0{,}1.
3. Comment peut-on en déduire le lieu géométrique du point \text{I} ?
2. Élaborer un programme écrit avec Python qui permet de calculer la longueur \text{OI} lorsque x varie entre 0 et 3 avec un pas de 0{,}1.
Cliquez pour accéder à une correction
3. Comment peut-on en déduire le lieu géométrique du point \text{I} ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
