Chapitre 10
Préparer le bac
Géométrie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Exercice guidé
[D'après Bac S - Pondichéry - 2016.]
L'objectif de cet exercice est de trouver une méthode pour construire à la règle et au compas un polygone régulier.
Dans le plan muni d'un repère orthonormé (\mathrm{O} ; \vec{i},\vec{j}), on considère le pentagone régulier \mathrm{A}_{0} \mathrm{A}_{1} \mathrm{A}_{2} \mathrm{A}_{3} \mathrm{A}_{4} de centre \text{O} tel que \overrightarrow{\mathrm{OA}_{0}}=\vec{i}.
On rappelle que dans le pentagone régulier ci-dessous :

Dans le plan muni d'un repère orthonormé (\mathrm{O} ; \vec{i},\vec{j}), on considère le pentagone régulier \mathrm{A}_{0} \mathrm{A}_{1} \mathrm{A}_{2} \mathrm{A}_{3} \mathrm{A}_{4} de centre \text{O} tel que \overrightarrow{\mathrm{OA}_{0}}=\vec{i}.
On rappelle que dans le pentagone régulier ci-dessous :

- les cinq côtés sont de même longueur ;
- les points \mathrm{A}_{0}, \mathrm{A}_{1}, \mathrm{A}_{2}, \mathrm{A}_{3} et \mathrm{A}_{4} appartiennent au cercle trigonométrique ;
- pour tout entier k appartenant à \{0\: ; 1\: ; 2 \:; 3\} , on a \left(\overrightarrow{\mathrm{OA}_{k}} \:; \overrightarrow{\mathrm{OA}_{k+1}}\right)=\dfrac{2 \pi}{5}.
1. On considère les points \mathrm{B}(-1\: ; 0) et \mathrm{J}\left(0\: ; \dfrac{1}{2}\right).
Le cercle \mathcal{C} de centre \text{J} et de rayon \dfrac{1}{2} coupe le segment \text{[BJ]} en un point \text{K.} Calculer \text{BJ} puis en déduire \text{BK.}
2. a. Exprimer à l'aide des fonctions cosinus et sinus les coordonnées du point \text{A}_2.
b. Démontrer que \left(\mathrm{BA}_{2}\right)^{2}=2+2 \cos \left(\dfrac{4 \pi}{5}\right).
Le cercle \mathcal{C} de centre \text{J} et de rayon \dfrac{1}{2} coupe le segment \text{[BJ]} en un point \text{K.} Calculer \text{BJ} puis en déduire \text{BK.}
Aide
Il est préférable de représenter la situation par une figure à main levée pour repérer les théorèmes à utiliser.
2. a. Exprimer à l'aide des fonctions cosinus et sinus les coordonnées du point \text{A}_2.
Aide
Il suffit de calculer une mesure de l'angle \left(\vec{i}, \overrightarrow{\mathrm{OA}_{2}}\right) puis de faire le lien entre les coordonnées de \text{A}_2 sur le cercle trigonométrique et le cosinus et le sinus.
b. Démontrer que \left(\mathrm{BA}_{2}\right)^{2}=2+2 \cos \left(\dfrac{4 \pi}{5}\right).
Aide
Il faut démontrer une égalité ici. Il suffit de partir du membre de gauche pour essayer de retrouver le membre de droite. Le membre de gauche est la longueur \mathrm{BA}_{2} élevée au carré : on utilise donc la formule de seconde permettant de calculer la distance entre deux points.
c. Un logiciel de calcul formel donne les résultats ci-dessous, que l'on pourra utiliser sans justification.

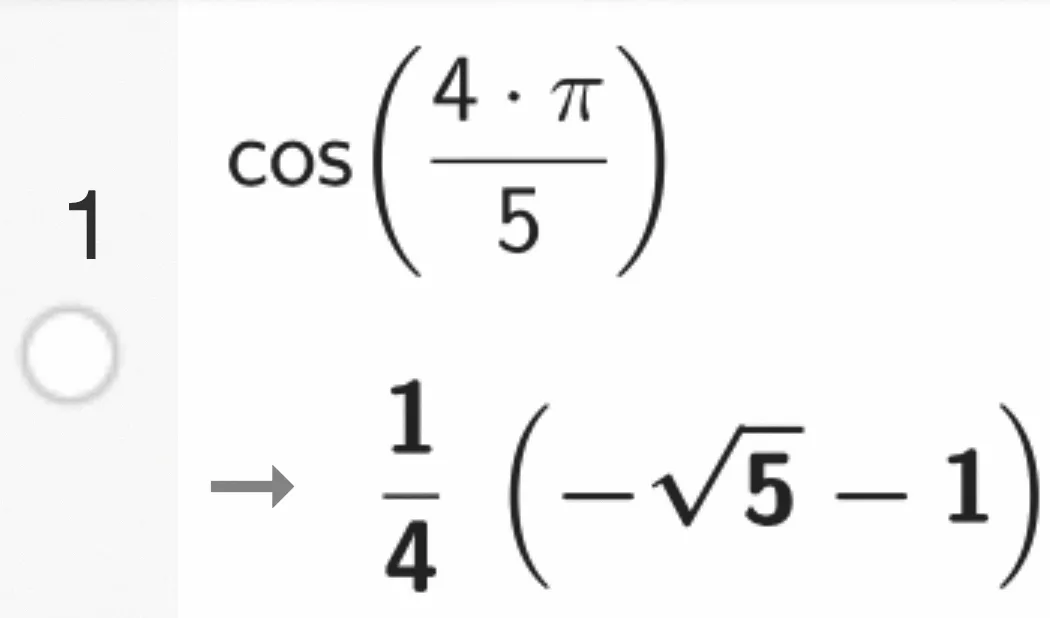

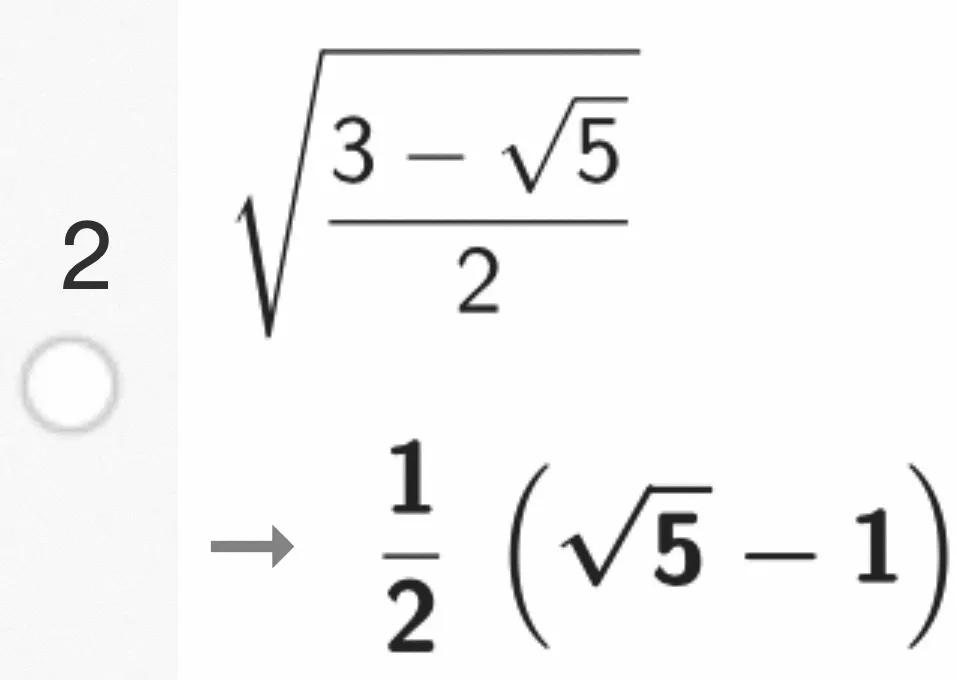
En déduire que \text{BA}_2 = \text{BK}.
3. Construire le pentagone régulier à la règle et au compas dans un repère orthonormé. N'utiliser ni le rapporteur ni les graduations de la règle et laisser apparents les traits de construction.

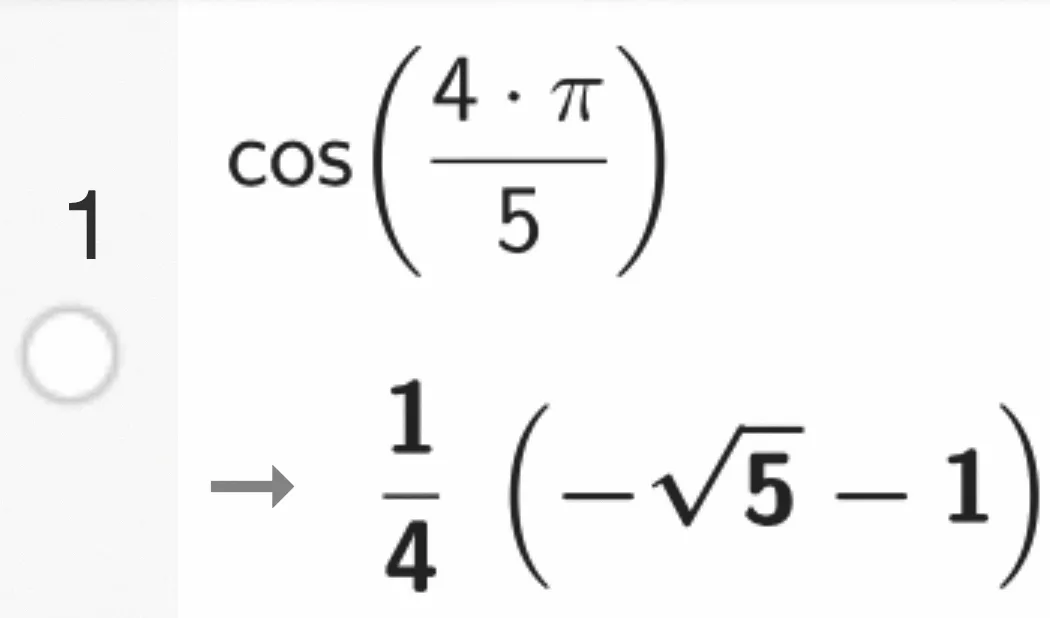

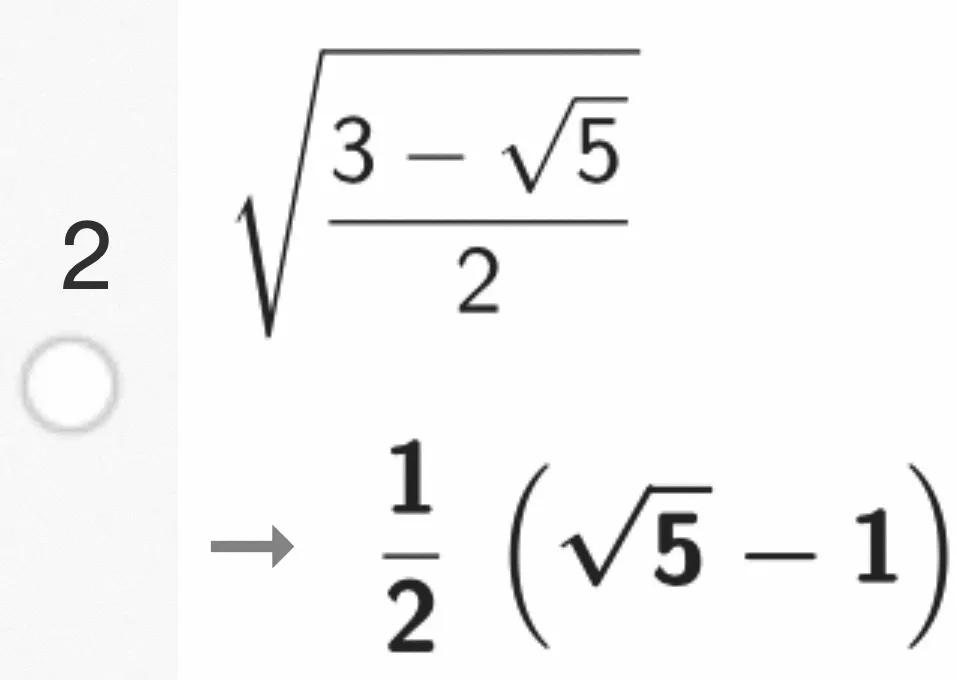
En déduire que \text{BA}_2 = \text{BK}.
Aide
On connaît la longueur \text{BK.} Il suffit donc de poursuivre le calcul de \text{BA}_2 en utilisant les expressions
données par le logiciel de calcul formel
3. Construire le pentagone régulier à la règle et au compas dans un repère orthonormé. N'utiliser ni le rapporteur ni les graduations de la règle et laisser apparents les traits de construction.
Aide
Pour représenter le pentagone, on utilise la question
précédente et le fait que le pentagone est régulier.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
[D'après Bac S - Liban - 2017.]
On considère un carré \text{ABCD} de côté 1. Le plan est rapporté au repère orthonormé (\mathrm{A} ; \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AD}}).
À tout réel de l'intervalle [0\: ; 1] , on associe le point \text{M} du segment \text{[DC]} tel que \overrightarrow{\mathrm{DM}}=x \overrightarrow{\mathrm{DC}}.

On s'intéresse à l'évolution de la mesure \theta en radian de l'angle \widehat{\mathrm{BMA}} lorsque le point \text{M} parcourt le segment \text{[DC].}
On a 0 \leqslant \theta \leqslant \dfrac{\pi}{2}.
À tout réel de l'intervalle [0\: ; 1] , on associe le point \text{M} du segment \text{[DC]} tel que \overrightarrow{\mathrm{DM}}=x \overrightarrow{\mathrm{DC}}.

On s'intéresse à l'évolution de la mesure \theta en radian de l'angle \widehat{\mathrm{BMA}} lorsque le point \text{M} parcourt le segment \text{[DC].}
On a 0 \leqslant \theta \leqslant \dfrac{\pi}{2}.
1. Que vaut \theta si le point \text{M} est confondu avec le point \text{D} ? Avec le point \text{C} ?
2. a. Justifier que les coordonnées du point \text{M} dans le repère (\mathrm{A} ; \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AD}}) sont (x\: ; 1).
b. Existe-t-il une position du point \text{M} sur le segment \text{[DC]} tel que le triangle \text{ABM} soit un triangle rectangle en \text{M} ?
c. En calculant de deux façons différentes le produit scalaire des vecteurs \overrightarrow{\mathrm{MA}} et \overrightarrow{\mathrm{MB}}, montrer que \cos (\theta)=\dfrac{x^{2}-x+1}{\sqrt{\left(x^{2}+1\right)\left(2-2 x+x^{2}\right)}}.
2. a. Justifier que les coordonnées du point \text{M} dans le repère (\mathrm{A} ; \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AD}}) sont (x\: ; 1).
b. Existe-t-il une position du point \text{M} sur le segment \text{[DC]} tel que le triangle \text{ABM} soit un triangle rectangle en \text{M} ?
c. En calculant de deux façons différentes le produit scalaire des vecteurs \overrightarrow{\mathrm{MA}} et \overrightarrow{\mathrm{MB}}, montrer que \cos (\theta)=\dfrac{x^{2}-x+1}{\sqrt{\left(x^{2}+1\right)\left(2-2 x+x^{2}\right)}}.
3. On s'intéresse à la fonction f définie sur l'intervalle [0\: ; 1] par f(x)=\dfrac{x^{2}-x+1}{\sqrt{\left(x^{2}+1\right)\left(2-2 x+x^{2}\right)}}.
On admet que sa dérivée est f^{\prime}(x)=\dfrac{2 x-1}{\sqrt{\left(x^{2}+1\right)\left(2-2 x+x^{2}\right)^{3}}}.
a. Étudier le signe de f'(x).
b. En déduire les variations de la fonction f sur son ensemble de définition.
4. a. Pour quelle position du point \text{M} sur le segment \text{[DC]} le nombre \cos(\theta) est-il minimal ?
b. Que peut-on en déduire pour l'angle \theta ? En déduire une valeur approchée de son extremum au centième de radian près et au centième de degré près.
On admet que sa dérivée est f^{\prime}(x)=\dfrac{2 x-1}{\sqrt{\left(x^{2}+1\right)\left(2-2 x+x^{2}\right)^{3}}}.
a. Étudier le signe de f'(x).
b. En déduire les variations de la fonction f sur son ensemble de définition.
4. a. Pour quelle position du point \text{M} sur le segment \text{[DC]} le nombre \cos(\theta) est-il minimal ?
b. Que peut-on en déduire pour l'angle \theta ? En déduire une valeur approchée de son extremum au centième de radian près et au centième de degré près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
[D'après Bac S - Nouvelle-Calédonie - 2018.]
On admet que, pour tous réels a et b, \cos (a+b)=\cos (a) \cos (b)-\sin (a) \sin (b) et \sin (a+b)=\sin (a) \cos (b)+\sin (b) \cos (a).
1. Après avoir vérifié que \dfrac{5 \pi}{12}=\dfrac{\pi}{4}+\dfrac{\pi}{6}, calculer les valeurs exactes de \cos \left(\dfrac{5 \pi}{12}\right) et \sin \left(\dfrac{5 \pi}{12}\right).
2. Résoudre l'équation suivante dans l'ensemble des réels \R :
(\sqrt{6}-\sqrt{2}) \cos (x)-(\sqrt{6}+\sqrt{2}) \sin (x)=-2 \sqrt{3}.
(\sqrt{6}-\sqrt{2}) \cos (x)-(\sqrt{6}+\sqrt{2}) \sin (x)=-2 \sqrt{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
[D'après Bac S - Centres étrangers - 2017.]
Le plan est muni d'un repère orthonormé (\mathrm{O} ; \vec{u}, \vec{v}).
Pour tout entier n \geqslant 4 , on considère \text{P}_n, un polygone régulier à n côtés, de centre \text{O} et dont l'aire est égale à 1.
On admet qu'un tel polygone est constitué de n triangles superposables à un triangle \mathrm{OA}_{n} \mathrm{B}_{n} donné, isocèle en \text{O.}
On note r_{n}=\mathrm{O} \mathrm{A}_{n} la distance entre le centre \text{O} et le sommet \mathrm{A}_{n} d'un tel polygone.
Pour tout entier n \geqslant 4 , on considère \text{P}_n, un polygone régulier à n côtés, de centre \text{O} et dont l'aire est égale à 1.
On admet qu'un tel polygone est constitué de n triangles superposables à un triangle \mathrm{OA}_{n} \mathrm{B}_{n} donné, isocèle en \text{O.}
On note r_{n}=\mathrm{O} \mathrm{A}_{n} la distance entre le centre \text{O} et le sommet \mathrm{A}_{n} d'un tel polygone.
Partie A : Étude du cas particulier n = 6
On a représenté ci-dessous un polygone \text{P}_6.

1. Justifier le fait que le triangle \mathrm{OA}_{6} \mathrm{B}_{6} est équilatéral, et que son aire est égale à \dfrac{1}{6}.
2. Exprimer en fonction de r_6 la hauteur du triangle \mathrm{OA}_{6} \mathrm{B}_{6} issue du sommet \mathrm{B}_{6}.
3. En déduire que r_{6}=\sqrt{\dfrac{2}{3 \sqrt{3}}}.
Partie B : Cas général avec n \geqslant 4
Dans cette partie, on considère le polygone \text{P}_n avec n \geqslant 4, construit de telle sorte que le point \text{A}_n soit situé sur l'axe des abscisses et ait pour abscisse r_n .
Le point \text{B}_n est obtenu à partir du point \text{A}_n par une rotation de centre \text{O} et d'angle \theta_n, où \theta_n est un réel de l'intervalle \left] 0\: ; \dfrac{\pi}{2} \right].

On a représenté ci-dessous un polygone \text{P}_6.

1. Justifier le fait que le triangle \mathrm{OA}_{6} \mathrm{B}_{6} est équilatéral, et que son aire est égale à \dfrac{1}{6}.
2. Exprimer en fonction de r_6 la hauteur du triangle \mathrm{OA}_{6} \mathrm{B}_{6} issue du sommet \mathrm{B}_{6}.
3. En déduire que r_{6}=\sqrt{\dfrac{2}{3 \sqrt{3}}}.
Partie B : Cas général avec n \geqslant 4
Dans cette partie, on considère le polygone \text{P}_n avec n \geqslant 4, construit de telle sorte que le point \text{A}_n soit situé sur l'axe des abscisses et ait pour abscisse r_n .
Le point \text{B}_n est obtenu à partir du point \text{A}_n par une rotation de centre \text{O} et d'angle \theta_n, où \theta_n est un réel de l'intervalle \left] 0\: ; \dfrac{\pi}{2} \right].

1. Exprimer en fonction de r_n et de \theta_n la hauteur issue de \text{B}_n dans le triangle \mathrm{OA}_{n} \mathrm{B}_{n} puis établir que l'aire de ce triangle est égale à \dfrac{\left(r_{n}\right)^{2}}{2} \times \sin \left(\theta_{n}\right).
2. On rappelle que l'aire du polygone \text{P}_n est égale à 1.
Donner, en fonction de n, une mesure de l'angle \left(\overrightarrow{\mathrm{OA}_{n}}, \overrightarrow{\mathrm{OB}_{n}}\right) puis démontrer que r_{n}=\sqrt{\dfrac{2}{n \sin \left(\dfrac{2 \pi}{n}\right)}}.
Partie C : Étude de la suite (r_n)
On considère la fonction f définie pour tout réel x de l'intervalle ]0\: ; \pi[ par f(x)=\dfrac{x}{\sin (x)}.
Ainsi, le nombre r_n, défini dans la partie B pour n \geqslant 4 , s'exprime à l'aide de la fonction f par : r_{n}=\sqrt{\dfrac{1}{\pi} f\left(\dfrac{2 \pi}{n}\right)}.
On admet que la fonction f est strictement croissante sur l'intervalle ]0\: ; \pi[ .
1. Montrer que la suite (r_n) est décroissante.
On pourra pour cela commencer par démontrer que, pour tout n \geqslant 4 , on a : 0 \lt \dfrac{2 \pi}{n+1} \lt \dfrac{2 \pi}{n} \lt \pi.
2. On considère l'algorithme suivant où n est un nombre entier non nul.
Quelle est la valeur numérique de n à la fin de cet algorithme ?
2. On rappelle que l'aire du polygone \text{P}_n est égale à 1.
Donner, en fonction de n, une mesure de l'angle \left(\overrightarrow{\mathrm{OA}_{n}}, \overrightarrow{\mathrm{OB}_{n}}\right) puis démontrer que r_{n}=\sqrt{\dfrac{2}{n \sin \left(\dfrac{2 \pi}{n}\right)}}.
Partie C : Étude de la suite (r_n)
On considère la fonction f définie pour tout réel x de l'intervalle ]0\: ; \pi[ par f(x)=\dfrac{x}{\sin (x)}.
Ainsi, le nombre r_n, défini dans la partie B pour n \geqslant 4 , s'exprime à l'aide de la fonction f par : r_{n}=\sqrt{\dfrac{1}{\pi} f\left(\dfrac{2 \pi}{n}\right)}.
On admet que la fonction f est strictement croissante sur l'intervalle ]0\: ; \pi[ .
1. Montrer que la suite (r_n) est décroissante.
On pourra pour cela commencer par démontrer que, pour tout n \geqslant 4 , on a : 0 \lt \dfrac{2 \pi}{n+1} \lt \dfrac{2 \pi}{n} \lt \pi.
2. On considère l'algorithme suivant où n est un nombre entier non nul.
\boxed{
\begin{array} { l } { \text {n} \leftarrow 4 } \\
\text {Tant que} \sqrt{\dfrac{2}{\text{n} \sin \left(\dfrac{2 \pi}{\text{n}}\right)}}>0{,}58 : \\
\quad \text {n} \leftarrow \text {n}+1 : \\
\text {Fin Tant que}
\end{array}
}
Quelle est la valeur numérique de n à la fin de cet algorithme ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


