49
[Communiquer.]
Soit \text{ABC} un triangle. On note \text{I} le milieu de \text{[BC].}
Que dire de l'aire des triangles \text{ABI} et \text{AIC} ?

Aide

On pourra utiliser la hauteur issue de \text{A.}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

50
Démo
[Raisonner.]

Soient \mathrm{A}\left(x_{\mathrm{A}}\: ; y_{\mathrm{A}}\right) \mathrm{B}\left(x_{\mathrm{B}}\: ; y_{\mathrm{B}}\right) et \mathrm{C}\left(x_{\mathrm{C}} \:; y_{\mathrm{C}}\right) trois points distincts du plan. On note\text{ G,} le centre de gravité du triangle \text{ABC.}
Démontrer que les coordonnées de \text{G} sont \left(\dfrac{x_{\mathrm{A}}+x_{\mathrm{B}}+x_{\mathrm{C}}}{3}\: ; \dfrac{y_{\mathrm{A}}+y_{\mathrm{B}}+y_{\mathrm{C}}}{3}\right).

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

51
[Représenter.]
ABC est un triangle tel que \text{A}', \text{B}' et \text{C}' sont les milieux respectifs de \text{[BC],} \text{[AC]} et \text{[AB].} On note \text{G} le centre de gravité du triangle, puis \text{I} et \text{J} les milieux respectifs des segments \text{[BG]} et \text{[CG].}
Montrer que le quadrilatère \text{C}'\text{IJB}' est un parallélogramme.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

52
[Raisonner.]
Le plan est muni d'un repère orthonormé (\mathrm{O} ; \mathrm{I}, \mathrm{J}).
Soit x un réel. On considère le point \text{P} de coordonnées (x\: ; 0) et le point \text{Q} de coordonnées (0 \:; x). Montrer, à l'aide d'égalités de vecteurs ou des coordonnées, que la médiane issue de \text{O} dans le triangle \text{IOQ} est perpendiculaire à la droite \text{(JP).}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

53
[Réprésenter.]
On se place dans un triangle \text{ABC} quelconque et on note \text{I} le pied de la médiane issue de \text{A.}

1. Construire une figure et y placer le point \text{D} tel que \text{ABDC} soit un parallélogramme.

Cliquez pour accéder à une zone de dessin

Cette fonctionnalité est accessible dans la version Premium.

2. Que peut-on dire de \text{I} pour le parallélogramme \text{ABDC} ?

3. Donner un vecteur égal à \overrightarrow{\mathrm{AC}}.

4. Montrer que \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}=2 \overrightarrow{\mathrm{AI}}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

54
Démo
[Communiquer.]
Dans le carré \text{ABCD,} on note \text{E} et \text{F} les milieux respectifs des segments \text{[AB]} et \text{[AD].} On note \text{I} le pied de la médiane issue de \text{A} dans le triangle \text{ADE.}
On souhaite démontrer que les droites \text{(AI)} et \text{(BF)} sont perpendiculaires.

1. Exprimer \overrightarrow{\mathrm{AI}} en fonction de \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{AD}}.

2. Calculer \overrightarrow{\mathrm{AI}} \cdot \overrightarrow{\mathrm{BF}} puis conclure.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

55
[Calculer.]

Dans le triangle \text{ABC,} on note \text{A}' le milieu de \text{[BC].} On donne les mesures suivantes : \text{AA}' = 6, \text{A}'\text{B} = 4 et \left(\overrightarrow{\mathrm{A}^{\prime} \mathrm{A}}, \overrightarrow{\mathrm{A}^{\prime} \mathrm{B}}\right)=\dfrac{\pi}{3}.

1. À l'aide d'une des formules du théorème de la médiane, calculer \mathrm{AB}^{2}+\mathrm{AC}^{2}.

2. a. Calculer \overrightarrow{\mathrm{A}^{\prime} \mathrm{A}} \cdot \overrightarrow{\mathrm{A}^{\prime} \mathrm{B}}.

b. Écrire \overrightarrow{\mathrm{CB}} en fonction de \overrightarrow{\mathrm{A}^{\prime} \mathrm{B}}.

c. En déduire \overrightarrow{\mathrm{CB}} \cdot \overrightarrow{\mathrm{AA}^{\prime}} et \mathrm{AB}^{2}-\mathrm{AC}^{2}.

3. Quelles sont alors les longueurs des côtés du triangle \text{ABC} ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

56
[Calculer.]
On définit un triangle \text{ABC} par les mesures de ses côtés : \text{AB} = 7, \text{AC} = 3 et \text{BC} = 8. On note \text{I} le milieu de \text{[BC].} Quelle est la longueur \text{AI} ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

57
Démo
[Communiquer.]
On se place dans un triangle \text{ABC} rectangle en \text{A.} En utilisant deux méthodes différentes, démontrer que la médiane issue de \text{A} mesure la moitié de la longueur du côté \text{[BC].}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

58
[Calculer.]
Soit \text{ABCD} un parallélogramme tel que \text{AB} = 15, \text{BC} = 13 et \text{AC} = 14.

1. Déterminer la longueur \text{BD.}

2. En déduire une mesure de l'angle \widehat{\mathrm{ABC}} arrondie au degré près.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

59
GeoGebra
[Calculer.]
On considère la figure suivante qui a été réalisée avec GeoGebra.

Le zoom est accessible dans la version Premium.

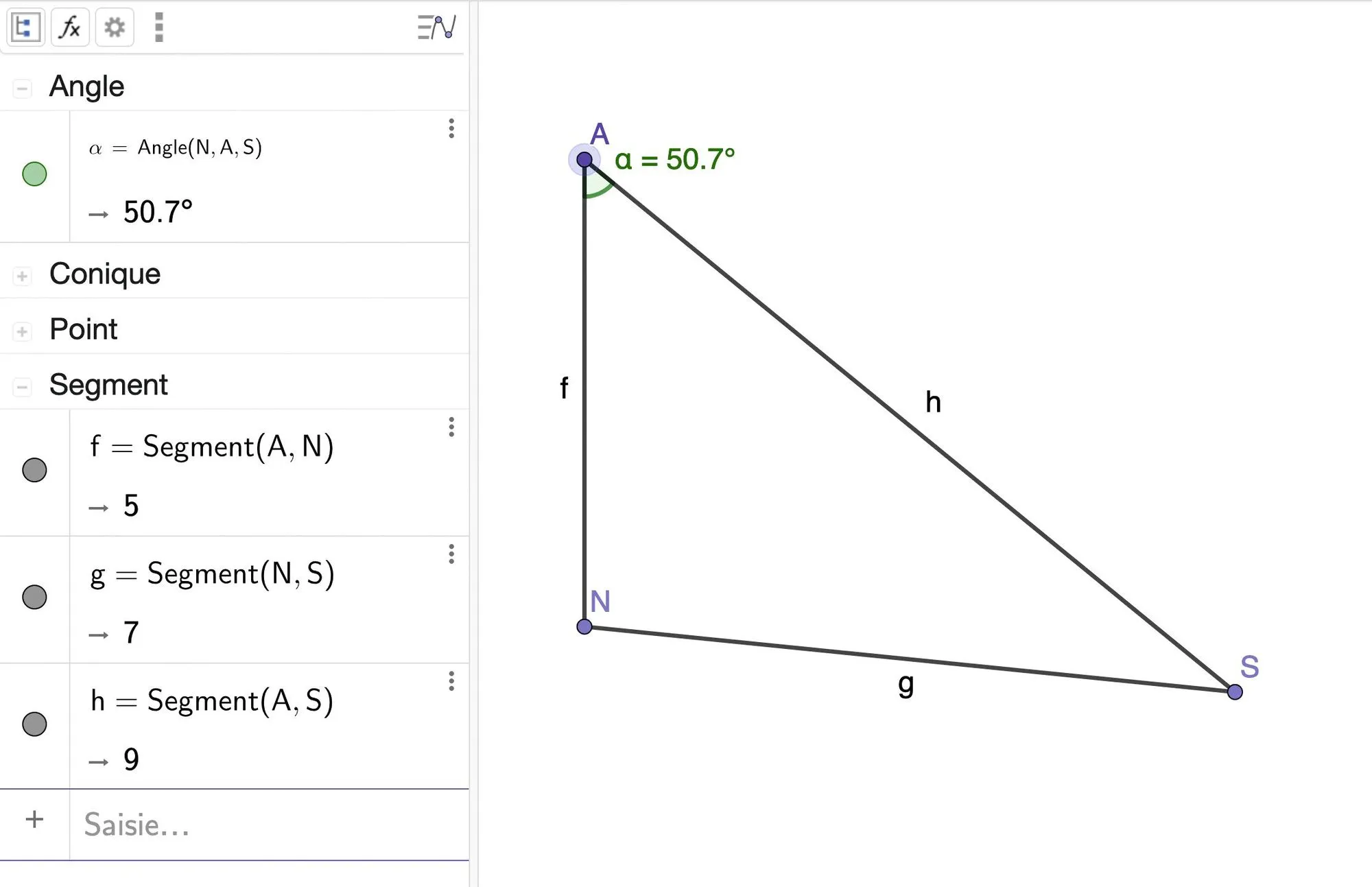
Retrouver, par le calcul, la valeur de l'angle \alpha déterminée par le logiciel.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

60
[Chercher.]
On considère les points \text{R}(3\: ; 5), \text{S}(1 \:; 10) et \text{G}(5\: ; 1). Trouver les coordonnées du point \text{T} telles que le triangle \text{TRS} admette le point \text{G} comme centre de gravité.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.