Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 2
Entraînement
Questions Flash
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
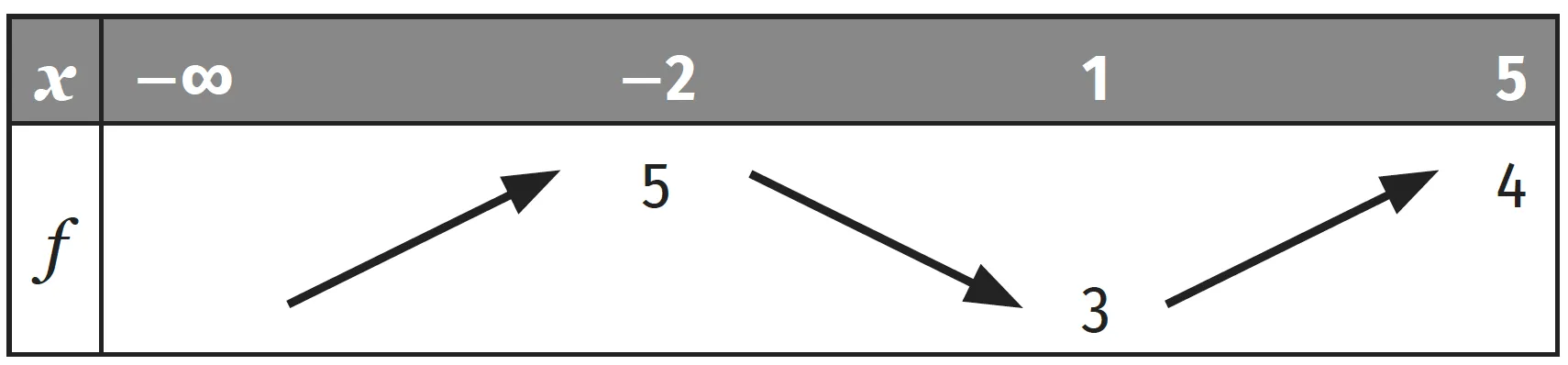
On considère le tableau de variations d'une
fonction f .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
1.
Préciser l'ensemble de définition \text{D} de f .2. En utilisant les termes « croissante » et « décroissante », décrire les variations de f .
3. Peut-on affirmer que :
a. 5 est le maximum de f sur \text{D} ?
b. 3 est le minimum de f sur \text{D} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
1. Comparer, en justifiant, les nombres suivants.
a. f(-10) et f(-5)
b. f(0) et f(1)
c. f(2) et f(3)
2. Est-il possible de comparer f(-4) et f(0) ? Justifier.
3. Quelles sont toutes les images que l'on peut comparer à f(1) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Dans le repère orthonormé, tracer une possible
courbe représentative de f .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Dans le repère orthonormé, tracer une courbe
représentative possible de la fonction g définie sur
\text{D} par g(x)=f(x)-4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
On considère ci-dessous la représentation graphique des fonctions f (en rouge) et g (en vert) dans un repère orthonormé.
1.
Dresser le tableau de variations de chacune de ces
deux fonctions sur \mathbb{R}.
Cliquez pour accéder à une zone de dessin
2.
Résoudre dans \mathbb{R} les inéquations suivantes.
a.f(x) \leqslant 3\:; f(x)>0
b. g(x) \leqslant 0 \:; g(x)>-2
c. f(x) \geqslant g(x)
a.f(x) \leqslant 3\:; f(x)>0
b. g(x) \leqslant 0 \:; g(x)>-2
c. f(x) \geqslant g(x)
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah