Études comparatives

Parcours 1 : exercices

28

;

32

;

39

et

53

Parcours 2 : exercices

30

;

37

;

40

;

47

et

60

Parcours 3 : exercices

42

;

49

;

50

;

57

et

61

35

[Raisonner.]
Soit f une fonction strictement croissante et définie sur \mathbb{R} telle que f(-2)=0 et f(1)=3. Déterminer l'intervalle des nombres réels x tels que :

1. f(x)\lt0

2. f(x) \geqslant 3

36

[Raisonner.] Soit g une fonction strictement décroissante et définie sur \mathbb{R} telle que g(0) = 1 et g(4) = -1. Déterminer l'intervalle des nombres réels x tels que -1\lt g(x) \leqslant 1.

38

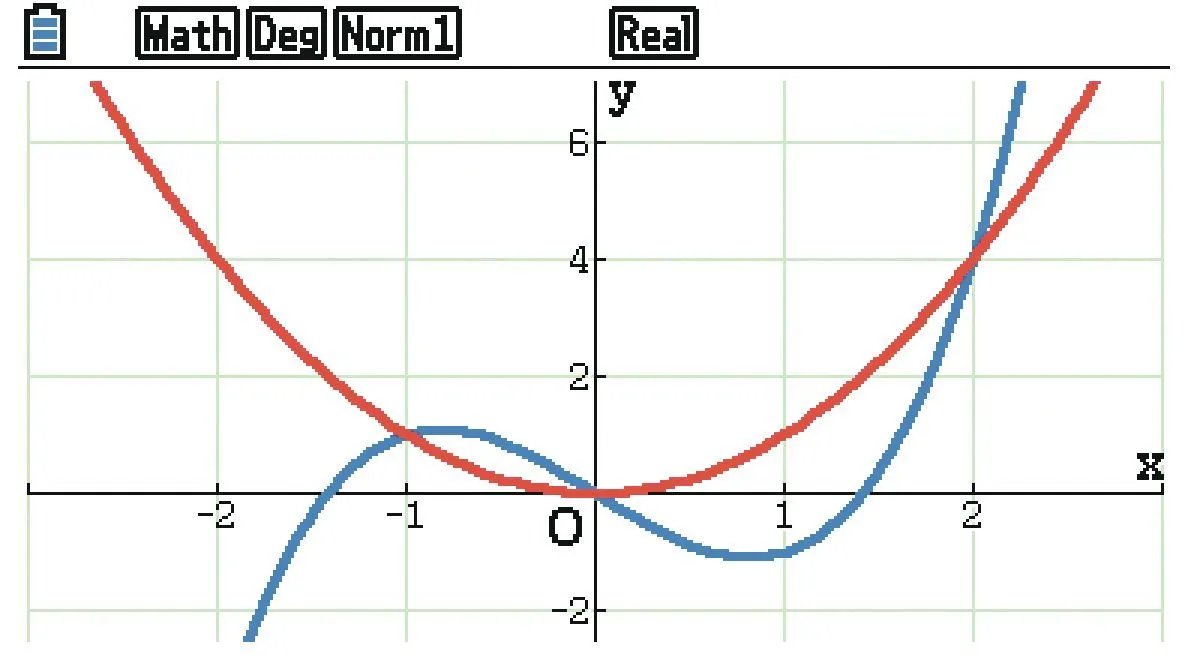
[Représenter.]
Charline a représenté deux fonctions f (en bleu) et g (en rouge) sur sa calculatrice.

Résoudre graphiquement dans \mathbb{R} l'inéquation f(x) \geqslant g(x).

39

[Raisonner.]
Dans un repère orthogonal, on a tracé la représentation graphique d'une fonction f définie sur un intervalle \text{I}.

1. Résoudre sur \text{I} l'inéquation f(x) > 4.

2. Résoudre sur \text{I}\: : 0 \leqslant f(x) \leqslant 4.

3. Indiquer le signe de f(x) suivant les valeurs de x \in \mathrm{I}.

41

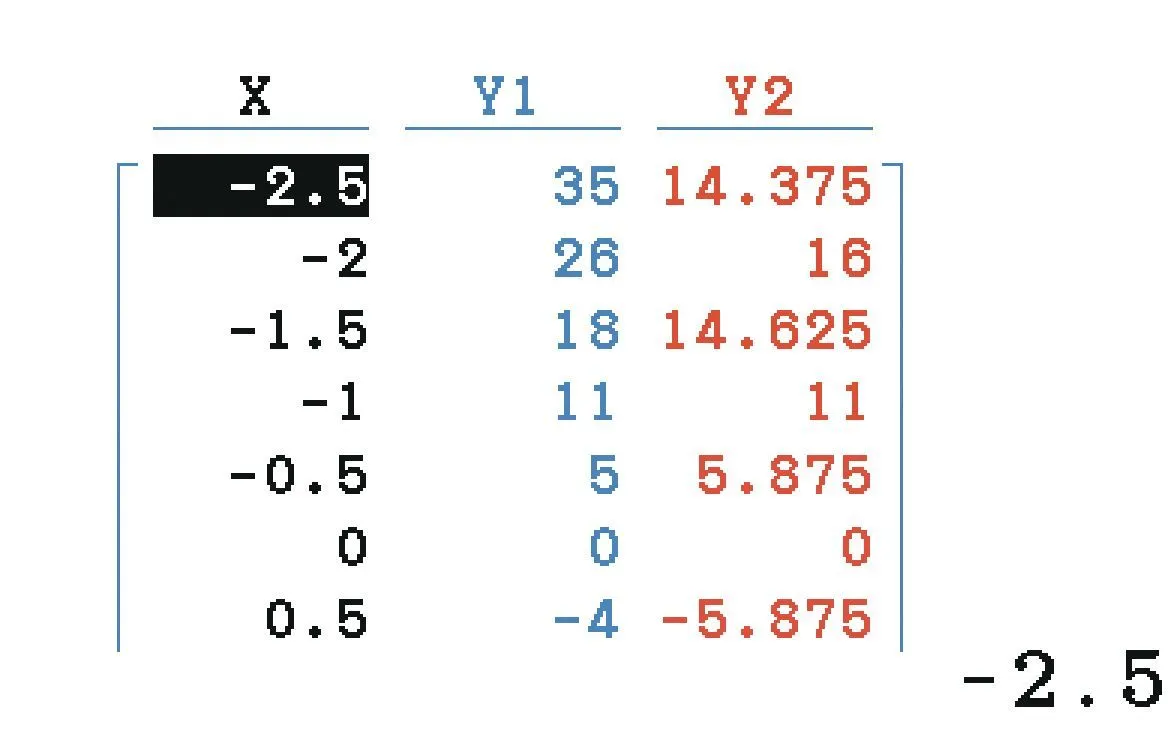
[Raisonner.]
On considère deux fonctions f et g définies sur [-2\text{,}5\:; 4] et dont on a affiché ci-dessous le tableau de valeurs obtenu à la calculatrice (\text{Y}_{1} pour f et \text{Y}_{2} pour g). Par lecture de ces tableaux de valeurs, conjecturer les valeurs de x sur [-2\text{,}5\:; 4] pour lesquelles on a :

1. f(x)=-4

2. f(x)=-10

3. f(x)\lt 0

4. f(x) = 0

5. g(x) = 16

6. f(x) = g(x)

7. f(x) \geqslant g(x)

8. f(x) \leqslant g(x)

42

[Modéliser.]
Sur une feuille A4 (21 \times 29,7 cm), un rédacteur souhaite placer une image carrée de longueur x , que l'on peut faire varier, ainsi qu'un texte explicatif à côté dans une zone de texte alignée avec l'image, avec des marges de 1 cm. Le texte explicatif occupe une aire de 80 cm² dans la zone de texte (il est possible que la zone de texte ait une aire supérieure à 80 cm²).

1. À quel intervalle \mathrm{I} appartient x\:?

2. Montrer que, pour tout x \in \mathrm{I}, l'aire \text{S} de la zone de texte est égale à \text{S}(x)=18 x-x^{2}.

3. Avec x =7, la zone de texte sera-t-elle suffisante ?

4. Le rédacteur se dit qu'il faut réduire x pour augmenter la largeur de la zone de texte. À l'aide de la courbe représentative de \text{S}:
a. résoudre \text{S}(x) = 80 ; \text{S}(x) > 80 ; \text{S}(x) \lt 80\:;

b. conclure sur la méthode du rédacteur.

47

[Chercher.]

49

[Modéliser.]
On considère les trois verres ci-dessous et on note h la hauteur en centimètre du liquide contenu dans chaque verre.

On note \text{V}_{1}(h), \text{V}_{2}(h) et \text{V}_{3}(h) les volumes respectifs de liquide dans ces trois verres en fonction de h. On a tracé dans un repère orthogonal les différentes courbes représentatives des fonctions \text{V}_{1}, \text{V}_{2} et \text{V}_{3}.

1. Pour chacun de ces trois verres, préciser les hauteurs telles que le volume du liquide soit strictement inférieur à 20 cm³.

2. Résoudre et interpréter : \mathrm{V}_{1}(h) \lt \mathrm{V}_{2}(h) ; \mathrm{V}_{1}(h) \lt \mathrm{V}_{3}(h) et \mathrm{V}_{2}(h) \lt \mathrm{V}_{3}(h).

3. a. Préciser, en fonction de la valeur de h , le verre ayant le plus faible volume de liquide.

b. Même question avec le plus grand volume de liquide.

52

[Modéliser.]
On a relevé la température de l'eau T en degré Celsius dans une casserole à feu léger, en fonction du temps t en minute, avec couvercle (A en rouge) et sans couvercle (S en vert) durant 15 min.
1. Déterminer et interpréter A(0) et S(0).

2. a. On suppose que 4 \lt t \lt 5 : encadrer A(t) et S(t).

b. La température de l'eau est comprise entre 70 et 80 °C : encadrer t dans les deux cas.

3. La cuisson d'un aliment doit s'arrêter lorsque T = 90 °C : indiquer le gain de temps en mettant un couvercle.

53

Une grande enseigne commercialise des étagères formée de cinq planches en bois identiques et d'un fond en bois (voir dessin). On note x et y les dimensions variables en centimètre des cinq planches, d'épaisseur négligeable. L'aire totale du bois utilisé est fixée à 7\,500 cm².


Pour x > 0, on peut montrer que y=\dfrac{7\,500-x^{2}}{5 x} et que le volume \text{V} de l'étagère est tel que : \text{V}(x)=\dfrac{7\,500 x-x^{3}}{5}.
On a représenté dans un repère orthogonal la courbe de la fonction \text{V}.


1. Lire la valeur de x telle que \text{V} soit maximale puis calculer y.

2. L'enseigne veut commercialiser des étagères d'un volume supérieur ou égal à 40\,000 cm³ : traduire cela par une inéquation et la résoudre graphiquement.

54

[Représenter.]
On reprend l'exercice précédent et on ajoute une planche supplémentaire (une 6^ème planche pour faire un rayon de rangement en plus). On note \text{W}(x) le volume de l'étagère correspondant. On admet alors que y=\dfrac{7\,500-x^{2}}{6 x} et que \mathrm{W}(x)=\dfrac{5}{6} \mathrm{V}(x) où \text{V}(x) est le volume de l'exercice

53

.
1. Déduire le volume maximum \text{W} et les dimensions de l'étagère.

2. L'enseigne souhaite toujours avoir un volume d'étagère de 40\,000 cm³.
a. Montrer que \text{W}(x) = 40\,000 équivaut à \text{V}(x) = 48\,000 .

b. Déduire par lecture graphique les dimensions x et y correspondantes.

55

[Raisonner.]
Refaire l'exercice

53

mais, cette fois, on décide d'ajouter une planche carrée identique à la planche du fond pour pouvoir fermer l'étagère. Dans ce cas, y=\dfrac{7\,500-2 x^{2}}{5 x} et V(x)=\dfrac{7\,500 x-2 x^{3}}{5}.