Mathématiques 2de
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 2
Synthèse
Exercices de Synthèse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
En SES
Calculatrice
[Chercher.] Un couple contracte un prêt d'un montant de 20 000 € au taux de 6 % par an. Le couple choisi le nombre d'années t pendant lequel il souhaite rembourser ce prêt. On suppose que t > 0. On admet que la somme totale à rembourser après t années est donnée par la fonction \text{S} définie pour tout t > 0 par \mathrm{S}(t)=20 \, 000 \times 1{,}06^{t}. Comme il y a 12 mois dans l'année, le montant à rembourser chaque mois sera donc défini par la fonction \text{M} pour tout t > 0 par \mathrm{M}(t)=\dfrac{\mathrm{S}(t)}{12 t}.
1. Pour chaque fonction :
a. tracer sa courbe représentative sur ]0\:; 40] en choisissant la bonne fenêtre graphique ;
b. conjecturer le tableau de variations sur ]0 \:; 40].
a. tracer sa courbe représentative sur ]0\:; 40] en choisissant la bonne fenêtre graphique ;
b. conjecturer le tableau de variations sur ]0 \:; 40].
Cliquez pour accéder à une zone de dessin
2. Si le couple souhaite payer le moins possible chaque
mois, sur combien d'années doit-il emprunter ? Quelle
sera alors la somme totale à rembourser ?
3. a. Encadrer t tel que \mathrm{S}(t) \in[30\,000 \:; 40\,000].
b. Pour ces valeurs de t, en déduire alors un encadrement de \text{M}(t).
4. Un couple a un budget maximum de 300 € par mois :
a. Résoudre \text{M}(t) \leqslant 300 puis encadrer \text{S}(t).
b. Pourquoi, en pratique, t \in[10 \: ; 17] ? Encadrer alors \text{S}(t) .
3. a. Encadrer t tel que \mathrm{S}(t) \in[30\,000 \:; 40\,000].
b. Pour ces valeurs de t, en déduire alors un encadrement de \text{M}(t).
4. Un couple a un budget maximum de 300 € par mois :
a. Résoudre \text{M}(t) \leqslant 300 puis encadrer \text{S}(t).
b. Pourquoi, en pratique, t \in[10 \: ; 17] ? Encadrer alors \text{S}(t) .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Modéliser.]
L'unité de longueur est le centimètre. \text{ABC} est un triangle tel que \text{AB} = 8 . On appelle \text{J} le milieu de [\text{BC}] et \text{K} celui de [\text{AC}] . Les droites (\text{AJ}) et (\text{BK}) sont sécantes en \text{G}. \text{M} est un point mobile sur [\text{AB}] . La droite (\text{GM}) coupe un autre côté du triangle en \text{N}. On note x = \text{AM} avec x \in[0\:; 8].

Les fonctions m : x \mapsto \mathrm{GM} et n : x \mapsto \mathrm{GN} sont représentées
dans le repère orthogonal ci-dessous.


1. Dresser le tableau de variations de m et de n sur l'intervalle [0\:; 8].
Cliquez pour accéder à une zone de dessin
2. Résoudre graphiquement et interpréter n(x) = m(x) puis n(x) > m(x).
3. Comment peut-on déduire des questions précédentes les solutions de n(x) \lt m(x) ?
3. Comment peut-on déduire des questions précédentes les solutions de n(x) \lt m(x) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
[Modéliser.]
On considère une roue de centre \text{C} et un rayon [\text{CM}].
Le point \text{M} décrit une courbe appelée cycloïde, dessinée en rouge dans le schéma ci-dessous.


On note f la fonction ainsi représentée dans le repère orthonormé ci-dessous :


1. Quel est le rayon du cercle ? En déduire le périmètre
du cercle puis l'ensemble de définition de f.
2. Tracer le tableau de variations de f sur son ensemble de définition.
2. Tracer le tableau de variations de f sur son ensemble de définition.
Cliquez pour accéder à une zone de dessin
3. Pour quelles valeurs de x le point \text{M} se situe-t-il au-dessus de la trajectoire [\text{AB}] décrite par le centre de la roue ? Préciser l'inéquation résolue.
4. Quelle est la courbe décrite par le point \text{M} si la roue continue d'avancer après le point \text{B} ?
4. Quelle est la courbe décrite par le point \text{M} si la roue continue d'avancer après le point \text{B} ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
[Chercher.]
Un hangar a une forme rectangulaire \text{ABCD} avec \text{AB} = 100 m et \text{BC} = 200 m.
Pour surveiller ce hangar, on place une caméra au point
\text{M}, milieu de [\text{AD}] . Son angle de vision est de 30°.


On note x l'angle, en degré, balayé par son axe de
vision (\text{MN}) lors de la rotation de la caméra.


Dans un repère orthogonal, on trace la courbe représentative
de l'aire \text{S} du hangar observable en fonction de
x \in[0 \:; 180] (en bleu sur les dessins précédents).


1. a. Tracer le tableau de variations de \text{S} sur [0\:; 180] .
b. Pour quels angles la fonction atteint-elle ses extremums ? Préciser les points N correspondants.
Cliquez pour accéder à une zone de dessin
b. Pour quels angles la fonction atteint-elle ses extremums ? Préciser les points N correspondants.
2. a. Pour quels angles la caméra a-t-elle un angle de
vision de moins de 30° ?
b. Quelle est l'image de 15° ? En quels angles a-t-on la même aire ?
c. Quel est le minimum de \text{S} sur l'intervalle [15\:; 165]\:? Situer le point \text{N} correspondant.
3. Calculer l'aire de \text{ABCD} .
4. Pour quels angles la caméra balaye-t-elle plus de 20 % de l'aire du hangar ? Moins de 15 % ?
b. Quelle est l'image de 15° ? En quels angles a-t-on la même aire ?
c. Quel est le minimum de \text{S} sur l'intervalle [15\:; 165]\:? Situer le point \text{N} correspondant.
3. Calculer l'aire de \text{ABCD} .
4. Pour quels angles la caméra balaye-t-elle plus de 20 % de l'aire du hangar ? Moins de 15 % ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Chercher.] Solal part de son domicile situé en \text{O} pour se rendre à son bureau \text{E} situé à 6 km. On note x la distance parcourue par Solal sur la route durant son trajet. Deux antennes-relais \text{A} et \text{B} de son opérateur téléphonique sont situées à 1,2 km et 1 km de part et d'autre de la route (perpendiculairement aux points \text{C} et \text{D}).

Le but est d'étudier les zones dans lesquelles Solal pourra recevoir du réseau téléphonique.
On suppose que \text{OC} = \text{CD} = \text{DE} = 2 km. La position de Solal sur la route est représentée par le point \text{P}. Pour étudier l'intensité du signal reçu grâce aux antennes \text{A} et \text{B} , on considère les fonctions f et g définies sur \text{I} = [0\:; 6] par f(x)=\dfrac{10}{\mathrm{AP}^{2}} pour l'antenne \text{A} et par g(x)=\dfrac{10}{\mathrm{BP}^{2}} pour l'antenne \text{B}.
1. Montrer que, pour tout x \in \text{I}, f(x)=\dfrac{10}{1{,}44+(2-x)^{2}} et g(x)=\dfrac{10}{1+(4-x)^{2}}.
2. On a tracé les courbes représentatives des fonctions f et g dans un même repère.

a. Tracer le tableau de variations de f et de g sur \text{I}.
2. On a tracé les courbes représentatives des fonctions f et g dans un même repère.

a. Tracer le tableau de variations de f et de g sur \text{I}.
Cliquez pour accéder à une zone de dessin
b. Préciser les valeurs de x maximisant f puis g :
pouvait-on trouver ces résultats par des considérations
géométriques ?
3. Sachant que le mobile capte le signal de l'antenne qui émet la plus grande intensité : préciser, suivant les valeurs de x, l'antenne qui sera captée par le mobile (en précisant les inéquations correspondantes).
4. En réalité, le réseau est reçu par le mobile lorsque l'intensité du signal est supérieure ou égale à 4.
a. Pour l'antenne \text{A} : quelle inéquation concernant f(x) cela revient-il à résoudre ? Préciser les valeurs de x correspondantes.
b. Répondre à la question précédente pour l'antenne \text{B}.
3. Sachant que le mobile capte le signal de l'antenne qui émet la plus grande intensité : préciser, suivant les valeurs de x, l'antenne qui sera captée par le mobile (en précisant les inéquations correspondantes).
4. En réalité, le réseau est reçu par le mobile lorsque l'intensité du signal est supérieure ou égale à 4.
a. Pour l'antenne \text{A} : quelle inéquation concernant f(x) cela revient-il à résoudre ? Préciser les valeurs de x correspondantes.
b. Répondre à la question précédente pour l'antenne \text{B}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
Calculatrice
[Chercher.]
Un élève a représenté les fonctions suivantes grâce à sa calculatrice graphique, en effectuant les réglages indiqués ci-après.
On précise l'expression de ces fonctions.
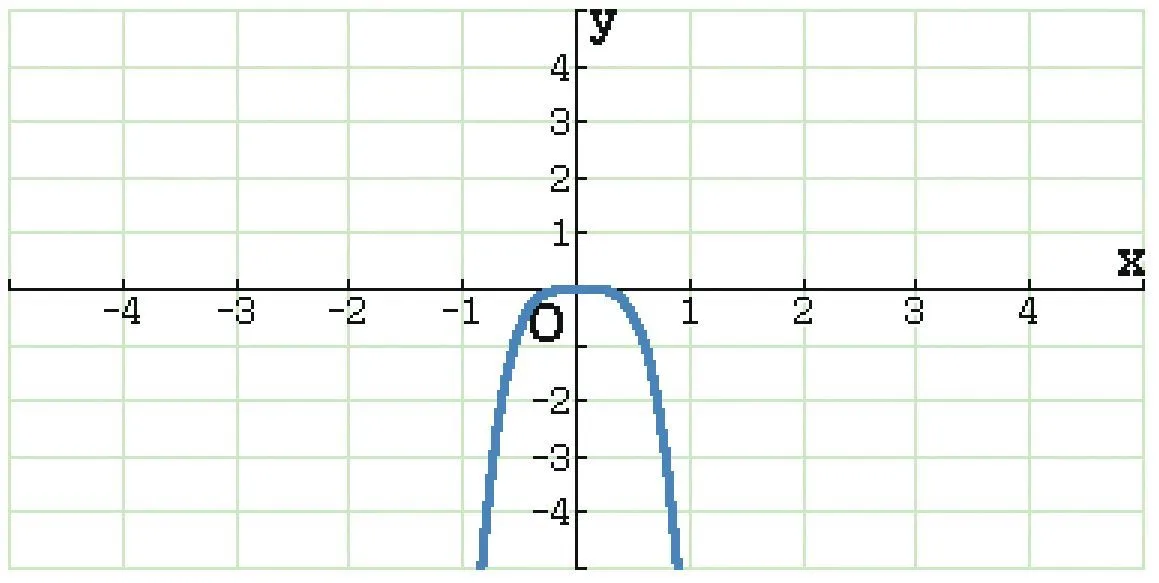
h(x)=-9 x^{4}+x^{3}







i(x)=1{,}54 x+\sqrt{\dfrac{1}{x}-1} (fonction définie sur ]0\:; 1])

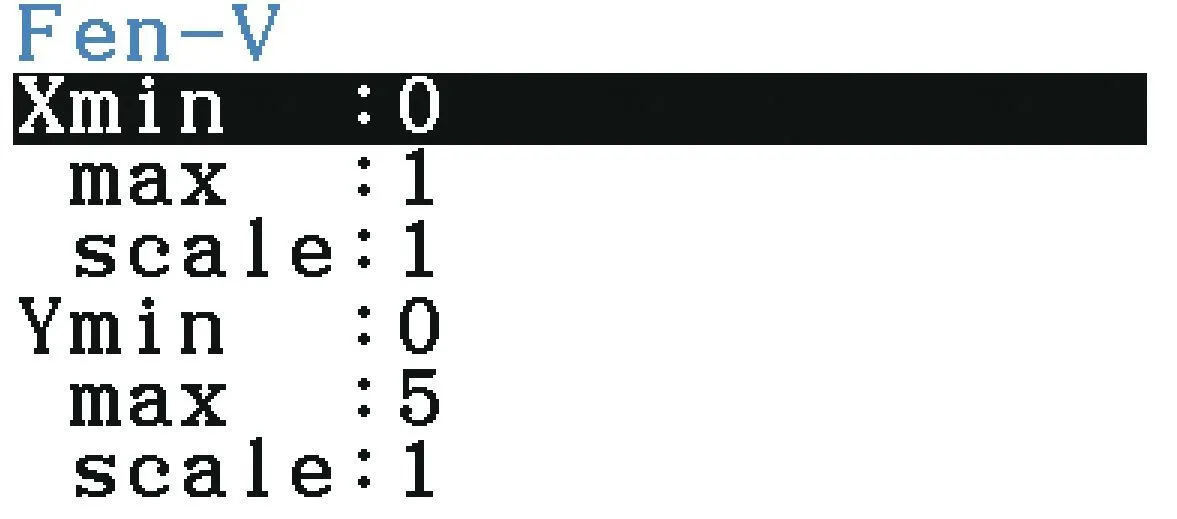

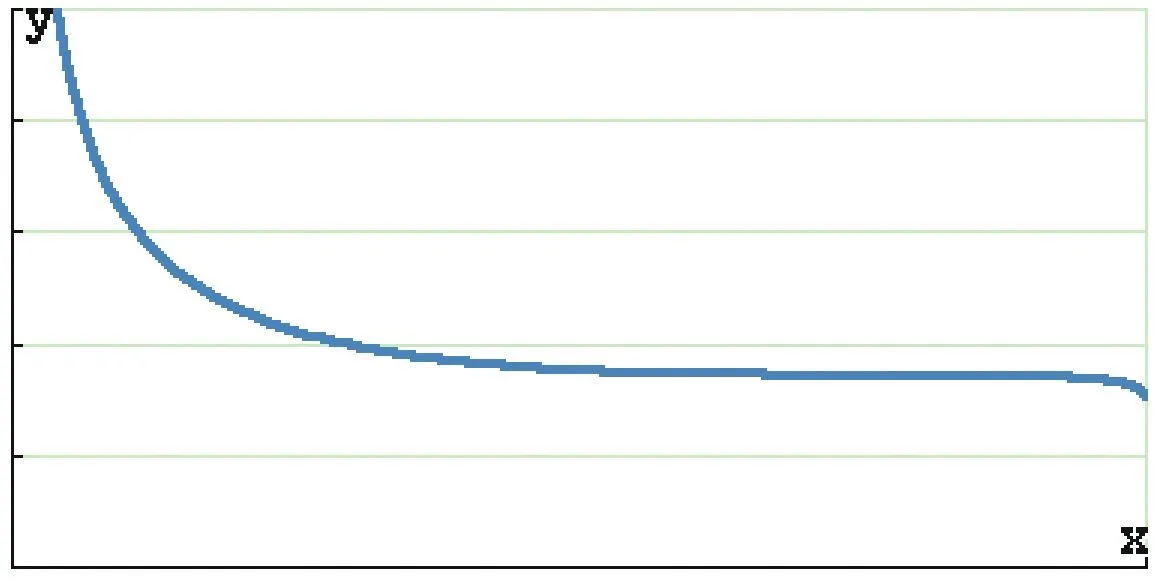




1. À partir de ces représentations graphiques, conjecturer
puis tracer les tableaux de variations de ces
différentes fonctions.
2. Pour la fonction h , on a changé la fenêtre graphique et on a obtenu la courbe ci-dessous.



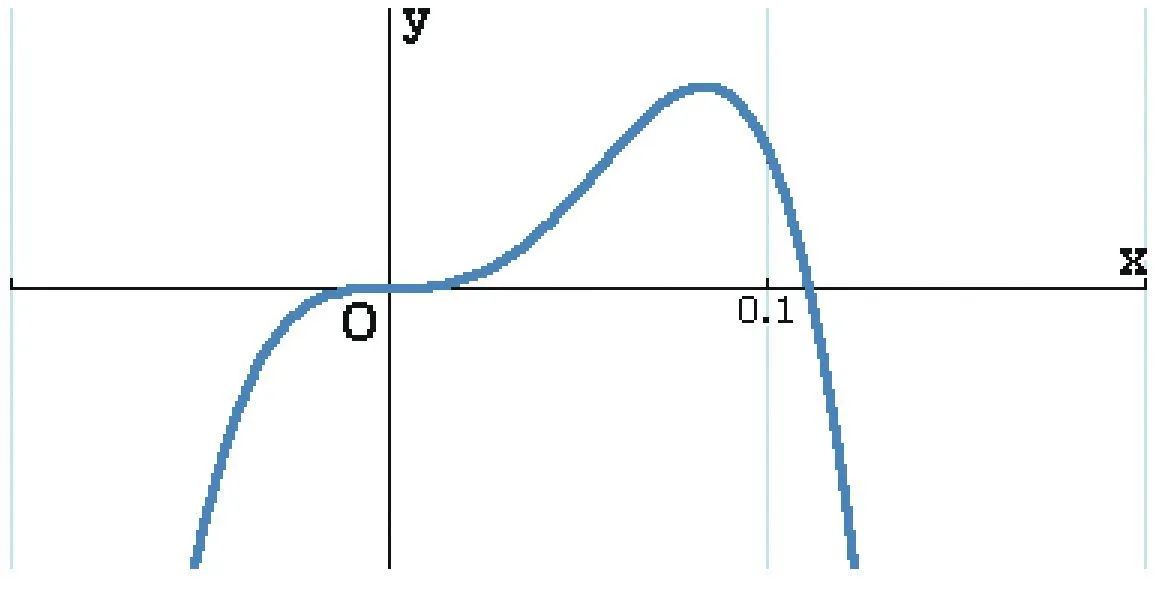
Rectifier le tableau de variations de h en conséquence. Comment expliquer les différences d'un réglage à l'autre ?
3.


Trouver un réglage avec lequel on peut observer les variations ci-dessus.
Cliquez pour accéder à une zone de dessin
2. Pour la fonction h , on a changé la fenêtre graphique et on a obtenu la courbe ci-dessous.




Rectifier le tableau de variations de h en conséquence. Comment expliquer les différences d'un réglage à l'autre ?
Cliquez pour accéder à une zone de dessin
3.
Défi
En réalité, comme pour la fonction h , les variations
de la fonction i ne sont pas correctement visibles
avec la fenêtre graphique choisie.


Trouver un réglage avec lequel on peut observer les variations ci-dessus.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Modéliser.]
Un segment [\text{AB}] de longueur égale à 6 glisse le long de deux axes perpendiculaires sécants en \text{O} . \text{C} et \text{D} sont les points de [\text{AB}] tels que \text{AD} = 1 et \text{BC} = 2 . On note x la longueur \text{OA} : ainsi, x \in[0\: ; 6].
Les fonctions f, g, h et p associent à chaque valeur de x \in[0\:; 6] respectivement les longueurs \text{OC}, \text{OD} et \text{CD} et le périmètre \text{P} du triangle \text{OCD}. On a tracé dans un repère les courbes représentatives de f , g , h et p .


1. Dresser les tableaux de variations de ces quatre fonctions
sur [0\:; 6].
2. a. Déterminer \text{OC} ; \text{OD} ; \text{CD} et \text{P} lorsque x = 2 .
b. Déterminer \text{OD} ; \text{CD} et \text{P} lorsque \text{OC} = 3{,}6 .
c. Le périmètre est égal à 9 : déterminer \text{OC} ; \text{OD} et \text{CD}.
Cliquez pour accéder à une zone de dessin
2. a. Déterminer \text{OC} ; \text{OD} ; \text{CD} et \text{P} lorsque x = 2 .
b. Déterminer \text{OD} ; \text{CD} et \text{P} lorsque \text{OC} = 3{,}6 .
c. Le périmètre est égal à 9 : déterminer \text{OC} ; \text{OD} et \text{CD}.
3. a. Déterminer les valeurs de x pour lesquelles \text{OCD}
est isocèle puis préciser les dimensions des triangles
correspondants.
b. \text{OCD} peut-il être équilatéral ? Justifier.
c. Préciser, suivant les valeurs de x , le plus petit puis le plus grand des côtés du triangle \text{OCD} .
d. Pourquoi peut-on affirmer que \text{OCD} ne peut pas être rectangle en \text{O}\: ?
4. En modifiant la fenêtre graphique de la courbe de p, on a obtenu le graphique suivant.

a. Modifier le tableau de variations de p en conséquence.
b. Déterminer x tel que p(x) > 10.
b. \text{OCD} peut-il être équilatéral ? Justifier.
c. Préciser, suivant les valeurs de x , le plus petit puis le plus grand des côtés du triangle \text{OCD} .
d. Pourquoi peut-on affirmer que \text{OCD} ne peut pas être rectangle en \text{O}\: ?
4. En modifiant la fenêtre graphique de la courbe de p, on a obtenu le graphique suivant.

a. Modifier le tableau de variations de p en conséquence.
Cliquez pour accéder à une zone de dessin
b. Déterminer x tel que p(x) > 10.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Club de Maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
Défi
Un point mobile \text{F} part d'un point \text{A} et fait le tour d'un rectangle de centre \text{O} . On note x la distance parcourue par \text{F} depuis \text{A} et d(x) la distance \text{OF}.

Préciser, uniquement grâce à la courbe représentative de d ci-après et en justifiant la démarche : 1. la longueur des diagonales et des côtés ;
2. le rayon des cercles de centre \text{O} et tangents à au moins un des côtés ; préciser alors si ces cercles coupent les autres côtés ;
3. les rayons des cercles de centre \text{O}:

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
Énigme
On considère un triangle \text{ABC} tel que \text{AB} = 8\: ; \text{BC} = 10\:; \text{CA} = 6 . \text{O} est le milieu de [\text{BC}].
Un point mobile \text{D} part de \text{A} et se déplace le long des côtés de \text{ABC}. On note x la longueur de son déplacement.
Dresser de façon exacte le tableau de variations de la fonction f : x \mapsto \mathrm{OD}.

Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
Casse-tête
Un professeur a demandé à ses élèves de mesurer sur un demi-cercle de centre \text{C} et de diamètre \text{AB} = 4 les longueurs \text{AM} et \text{IM} en fonction de x=\widehat{\mathrm{AIM}} (en degrés) où \text{I} est le milieu du rayon [\text{CS}] perpendiculaire à (\text{AB}) ; puis de tracer la courbe représentative des fonctions f et g correspondantes.
Le lendemain, il donne une interrogation surprise et Nathalie n'a pas fait son travail !
L'aider à répondre aux questions posées.

1. a. Sur quel intervalle les fonctions f et g sont-elles définies ?
b. Dresser leur tableau de variations.
b. Dresser leur tableau de variations.
Cliquez pour accéder à une zone de dessin
2. Indiquer, suivant les valeurs de k , le nombre de solutions de :
a. f(x)=k
b. g(x)=k
3. a. Justifier que f(x) = g(x) admet une unique solution que l'on notera x_{0}.
b. Résoudre f(x) \lt g(x) puis f(x) >g(x).
a. f(x)=k
b. g(x)=k
3. a. Justifier que f(x) = g(x) admet une unique solution que l'on notera x_{0}.
b. Résoudre f(x) \lt g(x) puis f(x) >g(x).
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
