Depuis 2010, les courses à obstacles connaissent une croissance impressionnante. En 2015, on estime à 180 000 le nombre de participants avec depuis une croissance de 20 % par an en moyenne.

Question préliminaire : Calculer \text{V}_{\text{A}}, le nombre de participants recherchés.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Course nature près lac, nombreux coureurs suivent chemin fleuri.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Objectif

Si l'évolution se poursuit ainsi, déterminer à partir de quelle année le nombre de participants aura augmenté de plus de 300 % par rapport à 2015 en utilisant une des trois méthodes.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 1
Python

On note \text{A} le nombre d'années écoulées depuis 2015. On note \text{N} le nombre de participants.

1. Recopier et compléter l'algorithme ci-dessous afin qu'il réponde à la question.

\boxed{ \begin{array} { l } \text{Définir Annee():} \\ \quad \text{A} \leftarrow 0 \\ \quad \text{N} \leftarrow 180\,000 \\ \quad \text {Tant que} \text { ...} : \\ \qquad \text{A} \leftarrow ... \\ \qquad \text{N} \leftarrow ... \\ \quad \text {Fin tant que} \\ \quad \text{Retourner(...)} \end{array} }

2. Programmer cet algorithme en Python et répondre à la question posée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 2
Tableur

On considère la feuille de calcul ci-dessous.

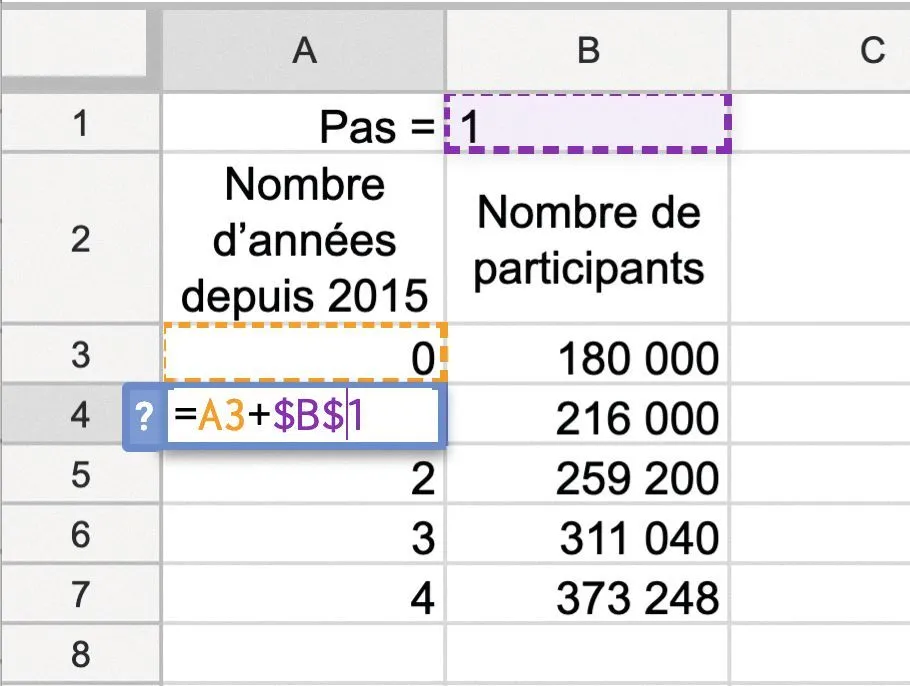
Capture d'écran tableau Excel calcul croissance participants 2015-2019. Formule : =A3+$B$1

1. Justifier la formule inscrite dans la cellule A4.

2. Quelle est la signification de PAS = 1 ? Que faudrait-il indiquer pour avoir une estimation chaque mois ?

3. Quelle formule faut-il inscrire dans la cellule B4 et ensuite étirer vers le bas ?

4. Reproduire cette feuille de calcul en utilisant les formules correctes et répondre alors au problème posé.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 3
Calculatrice

On note x le nombre d'années écoulées depuis 2015. On note f la fonction définie sur \mathbb{R} par f(x)=180\,000 \times 1{,}2^{x}.

1. a. Calculer f(1) et interpréter le résultat.

b. Retrouver l'expression de f lorsque x est un entier naturel.

2. Justifier que le problème se ramène à chercher la plus petite valeur de x telle que f(x)>720\,000.

3. La calculatrice affiche la courbe suivante.

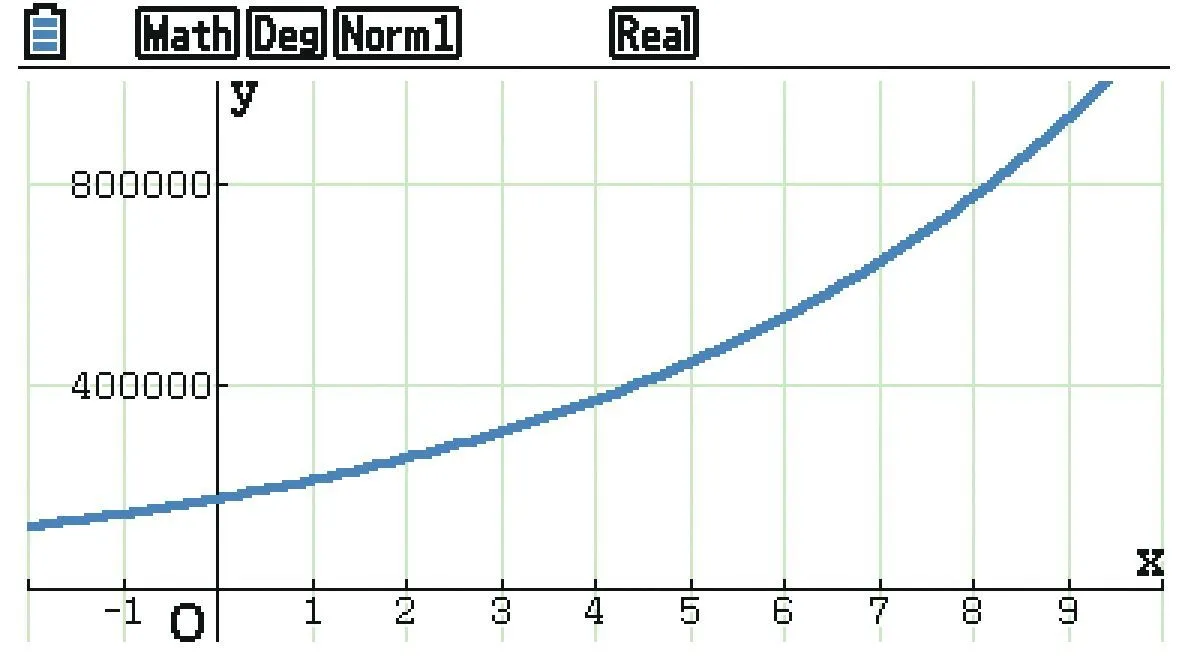
Graphique montrant une courbe exponentielle croissante.

a. Quelles manipulations peut-on faire pour estimer une réponse au problème à l'aide d'une lecture graphique ?

b. Conjecturer alors une réponse au problème.

4. a. Afficher le tableau de valeurs de la calculatrice et, à l'aide de ce tableau, retrouver la conjecture obtenue à la question précédente.

b. Conjecturer une valeur de x à 10^-1 près répondant au problème et interpréter le résultat.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Mathématiques 2de

Combien d'années pour atteindre l'objectif ?

Énoncé

Objectif

Méthode 1Python

Méthode 2Tableur

Méthode 3Calculatrice

Une erreur sur la page ? Une idée à proposer ?

Méthode 1
Python

Méthode 2
Tableur

Méthode 3
Calculatrice