Sommaire
Mes pages
N° Page
ouverture
p. 1-11
Fonctions
Géométrie
Statistiques et probabilités
Annexes
Nos dossiers d'actualité
Dossier d'actualité
/ 339
Page précédente
Chapitre 5
Activités

Repérage et configuration dans le plan

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Le bon repère

Connaître différents repères du plan.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
On considère les repères 1 et 2 définis par les cadres ci‑dessous et le repère 3 défini par le graphique ci‑après.

Repère 1
(\mathrm{OI}) \perp(\mathrm{OJ})
\mathrm{OI}=\mathrm{OJ}

Repère 2
(\mathrm{OI}) \perp(\mathrm{OJ})
\mathrm{OI}\neq\mathrm{OJ}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Repère 3

Repérage et configuration dans le plan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
Compléter l'encadré du repère 3 en reprenant le même modèle que les repères 1 et 2.
2
En utilisant le repère 3, donner, sans justification, les coordonnées des points \text{A ; B ; C ; D ; E ; F ; G} et \text{R .}

3
a) Reproduire la figure du repère 3 sans changer les coordonnées dans le repère 1 ci-dessous.
Le bon repère


b) Reproduire la figure du repère 3 sans changer les coordonnées dans le repère 2 ci-dessous.

Le bon repère

4
En comparant les trois repères, répondre aux questions suivantes.
a) Que peut-on dire du point \text{F}\:? Du point \text{R}\:?

b) Que peut-on dire du quadrilatère \text{ABCD}\:? Du triangle \text{AEB}\:?
c) Que peut-on dire des droites (\mathrm{AC}) et (\mathrm{EB})\:?
d) Que peut-on dire des points \text{F\:; G} et \text{R}\:?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Bilan

Cochez les cases correctes dans le tableau ci‑dessous

 Conservation dans le repère : Non conservation dans le repère :
 L'orthogonalité
 L'alignement et le parallélisme
 Les milieux
 Les distances


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Le radar défectueux : calculs de distance

Découvrir la formule du calcul de distance.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Deux avions de la compagnie Qatar Airways (\text{Q}) et de la compagnie Pegasus Airlines (\mathrm{P}) approchent de la tour de contrôle de l'aéroport d'Istanbul, en Turquie.
L'écran de contrôle de l'avion \text{Q} est défectueux : le cercle est centré sur la tour de contrôle, non visible, alors que le repère (\text{Q ; I , J}) est centré sur la position de l'avion.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Repérage et configuration dans le plan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
Reproduire le repère orthonormé (\text{Q ; I , J}) et placer les points \text{A , B} et \text{C} de coordonnées respectives (-5\:; 5),(-1\:;-3) et (4\:; 2). Tracer le triangle \text{ABC}.

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

2
Construire la médiatrice de chacun des segments [\mathrm{AB}],[\mathrm{BC}] et [\mathrm{AC}] . Que remarquez-vous ?


3
Déterminer graphiquement les coordonnées de \text{O}, point d'intersection des trois médiatrices.


4
a) Justifier l'égalité \mathrm{OA}=\mathrm{OB}=\mathrm{OC}=5
b) Que représente le point \text{O} géométriquement ? Et par rapport au contexte ?


5
Pour mesurer la distance \text{OQ} , on introduit le point \text{H} projeté orthogonal du point \text{O} sur (\mathrm{QI}) .
a) Justifier que le point \text{H} a pour coordonnées (-1\:; 0).
b) Démontrer que \mathrm{QO}^{2}=\left(x_{\mathrm{O}}-x_{\mathrm{Q}}\right)^{2}+\left(y_{\mathrm{O}}-y_{\mathrm{Q}}\right)^{2}
c) En déduire la distance \mathrm{QO}.
d) Calculer, de même, les distances \text{OP} et \text{QP}.

6
En déduire la distance réelle entre l'avion de la compagnie Pegasus Airlines et la tour de contrôle puis entre les deux avions sachant que la distance réelle entre l'avion de la compagnie Qatar Airways et la tour de contrôle est de 32 km.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Bilan

Dans un repère orthonormé, les points \text{A} et \text{B} ont pour coordonnées respectives \left(x_{\mathrm{A}}\:; {y}_{\mathrm{A}}\right) et \left(x_{B}\:; y_{B}\right) . En déduire une formule pour calculer la distance \text{AB} .

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

C
Algorithme et coordonnées du milieu d'un segment

Déterminer les coordonnées du milieu d'un segment.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

On munit le plan d'un repère quelconque (\text{O ; I , J}). On considère les points \text{A}(-1\:;-2) ; \text{B}(-2\:; 3) et \text{C}(4\:; 1). On cherche à déterminer les coordonnées du point \text{K} , milieu du segment [\mathrm{AB}] et du point \text{L} , milieu de [\mathrm{BC}].

Repérage et configuration dans le plan

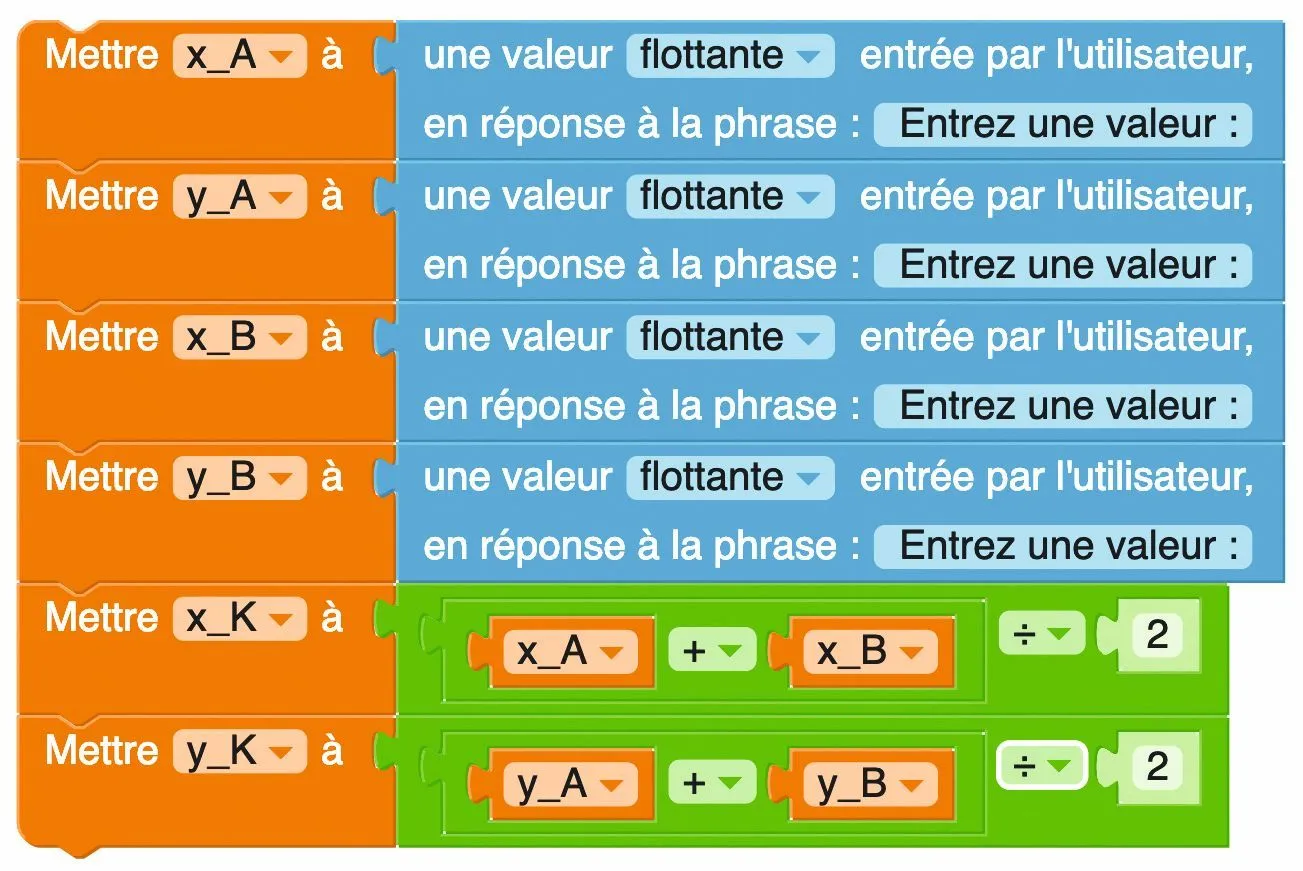
Dans une classe de seconde, Léo, Mélissa et Aïcha proposent les algorithmes de calculs suivants, réalisés avec des outils numériques différents.
  • Algorithme 1 : Léo a utilisé un tableur en écrivant, dans la cellule F2, la formule : =(\mathrm{D} 2+\mathrm{E} 2) / 2.
    Placeholder pour Capture d'écran tableau calcul géométrique: abscisse et ordonnée des points A, B et K. Formule de calcul du milieu K.Capture d'écran tableau calcul géométrique: abscisse et ordonnée des points A, B et K. Formule de calcul du milieu K.

  • Algorithme 2 : Mélissa a utilisé Pyblock ci-dessous.
    Placeholder pour Capture d'écran de blocs de code calculant des coordonnées. L'utilisateur entre des valeurs flottantes pour les points A et B, puis le code calcule les coordonnées du point K.Capture d'écran de blocs de code calculant des coordonnées. L'utilisateur entre des valeurs flottantes pour les points A et B, puis le code calcule les coordonnées du point K.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
  • Algorithme 3 : Aïcha a utilisé un programme en Python ci-après.
    def milieu (xA, yA, xB, yB):
	xK = xA + xB / 2
  yK = yA + yB / 2
  return(xK, yK)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
Placer le point \text{K}, milieu du segment \text{[AB]}, et le point \text{L}, milieu du segment \text{[BC],} sur l'image du repère \text{(O ; I ,J).}

2
Compléter le tableau ci‑dessous.
 x_\text{A} y_\text{A} x_\text{B} y_\text{B} x_\text{K} y_\text{K}
 Algo 1
 Algo 2
 Algo 3

3
Parmi les trois algorithmes, lesquels permettent d'afficher les coordonnées du point \text{K}\:?


4
Les algorithmes de la question
3
fonctionnent-ils pour le point \text{L}\:?


5
En déduire l'algorithme qui convient.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Bilan

Écrire les formules donnant les coordonnées du milieu \mathbf{K}\left(x_{\mathbf{K}}\:; {y}_{\mathbf{K}}\right) du segment [\mathbf{A B}] avec \mathbf{A}\left(x_{\mathrm{A}} ; \boldsymbol{y}_{\mathrm{A}}\right) et \mathbf{B}\left(x_{\mathbf{B}} ; \boldsymbol{y}_{\mathbf{B}}\right)


Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille