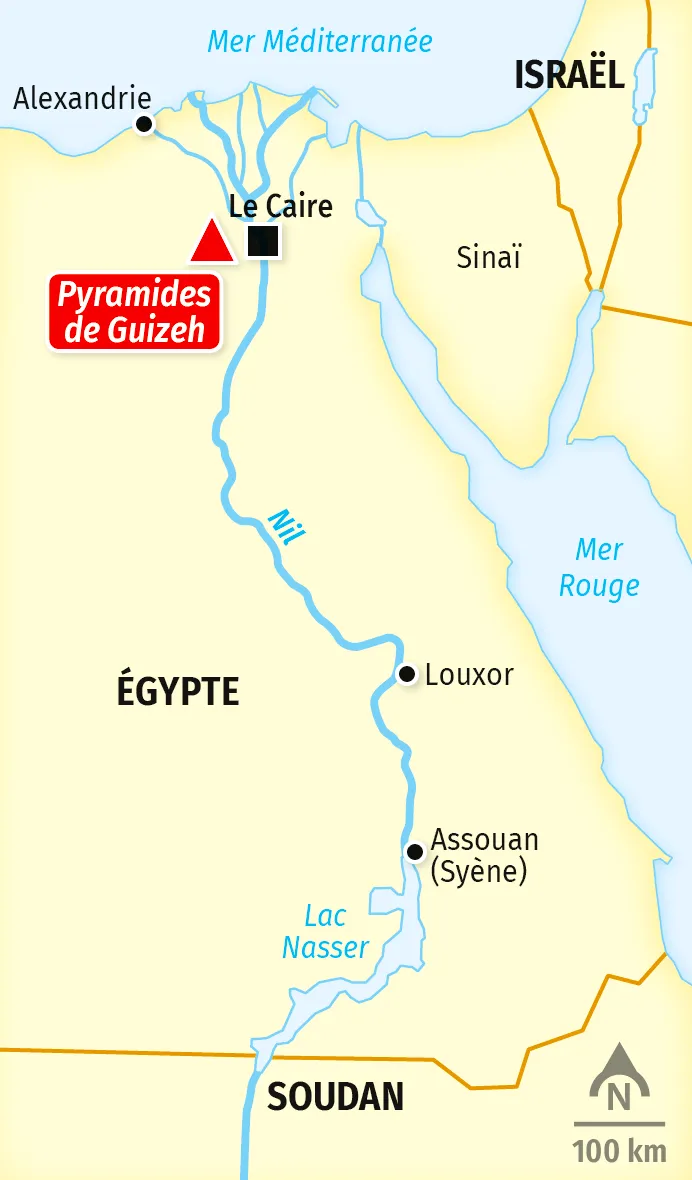
C'est à la bibliothèque d'Alexandrie qu'un papyrus a attiré l'attention d'Ératosthène. Il y a lu qu'à Syène, ville frontière au Sud, située près des premières chutes du Nil, à peu près sur le tropique du Cancer, le 21 juin à midi, un bâton planté à la verticale n'avait pas d'ombre. Il se pose alors la question suivante : pourquoi au même moment, beaucoup plus au Nord, à Alexandrie, un autre bâton, lui, en projette une (le Soleil étant à peu près à 7,2° du zénith) ?
Il suppose que le Soleil est assez éloigné pour que ses rayons frappent la surface terrestre en faisceaux parallèles. Ératosthène ne trouve qu'une seule réponse à sa question : la surface de la Terre est courbe !
Ce constat lui a permis de faire le calcul du rayon de la Terre après avoir mesuré la distance qui séparait Syène d'Alexandrie. Une légende raconte qu'il aurait déterminé cette distance en comptant des pas réguliers de chameaux et que ces mêmes chameaux auraient parcouru 5 000 stades égyptiens. La longueur d'un stade est de 157,5 m.