Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Thème 1 : Une longue histoire de la matière
Ch. 1
Les éléments chimiques
Ch. 2
Des édifices ordonnés : les cristaux
Ch. 3
Une structure complexe : la cellule
Thème 2 : Le Soleil, notre source d'énergie
Ch. 4
Le rayonnement solaire
Ch. 5
Le bilan radiatif terrestre
Ch. 6
Énergie solaire et photosynthèse
Ch. 7
Le bilan thermique du corps humain
Thème 3 : La Terre, un astre singulier
Ch. 8
La forme de la Terre
Ch. 9
L'histoire de l’âge de la Terre
Ch. 10
La Terre dans l’Univers
Thème 4 : Son et musique, porteurs d'information
Ch. 11
Le son, phénomène vibratoire
Ch. 12
Musique et nombres
Ch. 13
Le son, une information à coder
Ch. 14
Entendre la musique
Projet Experimental et Numérique
Livret Maths
Annexes
Chapitre 8
Le coin des experts
Le coin des experts
18 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5 Mesure du rayon de Mars
✔ Conduire un raisonnement quantitatif
.
Dans le film Seul sur Mars, l'astronaute Mark Watney est laissé pour mort par ses coéquipiers qui quittent la planète après une violente tempête. Mais Mark a survécu. Ses journées sont occupées par différentes activités en attendant qu'une mission vienne le récupérer. Il veut calculer le rayon de Mars avec du matériel basique. Il se positionne dans une zone très dégagée de tout relief. Il fixe un pointeur laser sur un support à la hauteur h= 1,70 m. Il pointe avec ce dispositif la pierre la plus lointaine qu'il puisse voir à l'horizon. La distance du laser à la pierre est : 3 395 m.
.
Dans le film Seul sur Mars, l'astronaute Mark Watney est laissé pour mort par ses coéquipiers qui quittent la planète après une violente tempête. Mais Mark a survécu. Ses journées sont occupées par différentes activités en attendant qu'une mission vienne le récupérer. Il veut calculer le rayon de Mars avec du matériel basique. Il se positionne dans une zone très dégagée de tout relief. Il fixe un pointeur laser sur un support à la hauteur h= 1,70 m. Il pointe avec ce dispositif la pierre la plus lointaine qu'il puisse voir à l'horizon. La distance du laser à la pierre est : 3 395 m.
1. Faites un schéma de son montage en traçant le
faisceau du rayon laser, jusqu'à la pierre, les rayons
de Mars au point de la pierre et au point de son
support tenant le laser.
2. Calculez, avec les mesures de Watney, la valeur du rayon de Mars.
3. Comparez cette valeur avec la valeur réelle de 3 390 km avec un calcul d'incertitude.
Cette fonctionnalité est accessible dans la version Premium.
2. Calculez, avec les mesures de Watney, la valeur du rayon de Mars.
3. Comparez cette valeur avec la valeur réelle de 3 390 km avec un calcul d'incertitude.
Doc.
Seul sur Mars de Ridley Scott (2015).
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6 Mesure de distance par visée et calcul de vitesse
✔ Exploiter et interpréter des mesures
Après une escale, le voilier Arpège quitte le rivage. Une personne sur la plage effectue des mesures par la méthode de visée afin de déterminer la distance qui le sépare du voilier. Il vise le voilier à travers une règle. Il tend son bras, de longueur 72 cm, une règle à la main, en visant le voilier. Il mesure la hauteur du voilier vue à travers sa règle : 1,3 cm (de la coque au haut du mât : 25 m en réalité).
Après une escale, le voilier Arpège quitte le rivage. Une personne sur la plage effectue des mesures par la méthode de visée afin de déterminer la distance qui le sépare du voilier. Il vise le voilier à travers une règle. Il tend son bras, de longueur 72 cm, une règle à la main, en visant le voilier. Il mesure la hauteur du voilier vue à travers sa règle : 1,3 cm (de la coque au haut du mât : 25 m en réalité).
1. Après avoir réalisé un schéma de la situation,
déterminez à quelle distance de la personne sur le rivage se trouve le voilier, en utilisant les relations
de proportionnalité énoncées dans le théorème de Thalès.
Cette fonctionnalité est accessible dans la version Premium.
2. Il effectue une seconde mesure 4 minutes plus tard.
La hauteur du voilier dans sa règle est de 0,9 cm. Calculez la distance qui le sépare maintenant du
voilier.
3. Calculez la distance parcourue par le voilier pendant cette durée.
4. Quelle a alors été la vitesse moyenne du voilier pendant cette durée ? Exprimez cette valeur en m·s‑1 puis en nœuds (1 nœud = 1,852 km·h‑1).
5. Le voilier finit par ne plus être visible. Que cela prouve-t-il quant à la forme de la Terre ?
3. Calculez la distance parcourue par le voilier pendant cette durée.
4. Quelle a alors été la vitesse moyenne du voilier pendant cette durée ? Exprimez cette valeur en m·s‑1 puis en nœuds (1 nœud = 1,852 km·h‑1).
5. Le voilier finit par ne plus être visible. Que cela prouve-t-il quant à la forme de la Terre ?
Doc.
Le voilier Arpège
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CDistance Terre-Lune par la méthode des parallaxes
✔ Conduire des raisonnements qualitatifs et quantitatifs
.
.
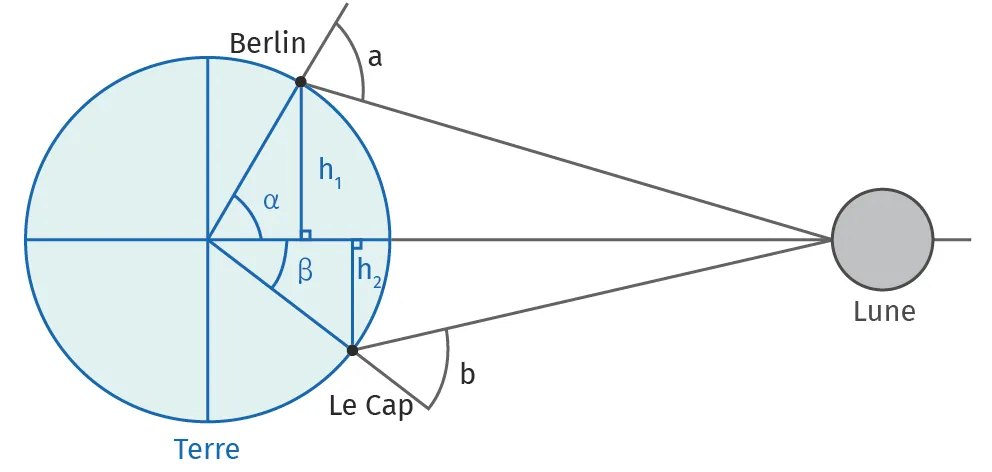
En 1751, Lalande se positionne à Berlin et Lacaille au Cap en Afrique du Sud. Ils observent chacun le centre du disque lunaire lors du passage au méridien de la Lune. Ils mesurent l'angle entre la verticale du lieu et le rayon provenant de la Lune.
1. Montrez que p, l'angle au sommet de la Lune, est lié à a, b, \alpha et \beta par p=(a+b)-(\alpha+\beta).
2. Montrez que la distance d_{BC} qui sépare Berlin du Cap égale à h_1+h_2, est également liée à R_T, sin \alpha et sin \beta par la relation : d_{BC}=R_T\cdot sin \alpha+R_T \cdot sin \beta.
3. Donnez l'expression de la tangente de p, tan(p), en fonction de et de la distance Terre-Lune d_{TL}.
4. Donner alors l'expression de la distance Terre-Lune d_\text{TL} en fonction de tan(p) et de d_\text{BC} pour montrer que d_\text{TL} = \text R_\text T \cdot (\sin \alpha + \sin \beta) + \tan p
5. Calculer d_\text{TL} .
Rayon de la Terre : R_T = 6 370 km
1. Montrez que p, l'angle au sommet de la Lune, est lié à a, b, \alpha et \beta par p=(a+b)-(\alpha+\beta).
2. Montrez que la distance d_{BC} qui sépare Berlin du Cap égale à h_1+h_2, est également liée à R_T, sin \alpha et sin \beta par la relation : d_{BC}=R_T\cdot sin \alpha+R_T \cdot sin \beta.
3. Donnez l'expression de la tangente de p, tan(p), en fonction de et de la distance Terre-Lune d_{TL}.
4. Donner alors l'expression de la distance Terre-Lune d_\text{TL} en fonction de tan(p) et de d_\text{BC} pour montrer que d_\text{TL} = \text R_\text T \cdot (\sin \alpha + \sin \beta) + \tan p
5. Calculer d_\text{TL} .
Données
| Ville | Latitude | Angle |
| Berlin | \alpha = 52,5° Nord | a = 53,32 ° |
| Cap | \beta = 33,9° Sud | b = 34,66° |
Rayon de la Terre : R_T = 6 370 km
Doc. 1
Schéma pour calculer la distance Terre-Lune
Le zoom est accessible dans la version Premium.
Doc. 2
Éclipse lunaire du 31 janvier 2018 vue du Parc naturel
régional des Vosges du Nord
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah