Mathématiques Expertes Terminale
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 7
TP Info 2
Algorithme de PageRank
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
On considère le graphe orienté ci‑contre. Un internaute est placé initialement à t=0 sur le site a. Chaque minute, il choisit un site vers lequel il se dirige. Chaque lien possible est équiprobable : ainsi, à t=1, il a une probabilité égale à 0{,}5 d'être en b et une probabilité égale à 0{,}5 d'être en d.

Question préliminaire :
1. Quelle est la probabilité d'être en c au temps t=2 ?
2. Quelle est la probabilité d'être en a au temps t=2 ?
En assimilant les probabilités aux fréquences obtenues au bout d'un temps très long, on attribue une pondération à chaque sommet du graphe qui permet de classer les sites.
1. Quelle est la probabilité d'être en c au temps t=2 ?
2. Quelle est la probabilité d'être en a au temps t=2 ?
En assimilant les probabilités aux fréquences obtenues au bout d'un temps très long, on attribue une pondération à chaque sommet du graphe qui permet de classer les sites.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Découvrir un algorithme PageRank à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
1. Écrire la matrice de transition \mathrm{P} associée au graphe probabiliste.
2. a. Recopier la feuille de calcul suivante.

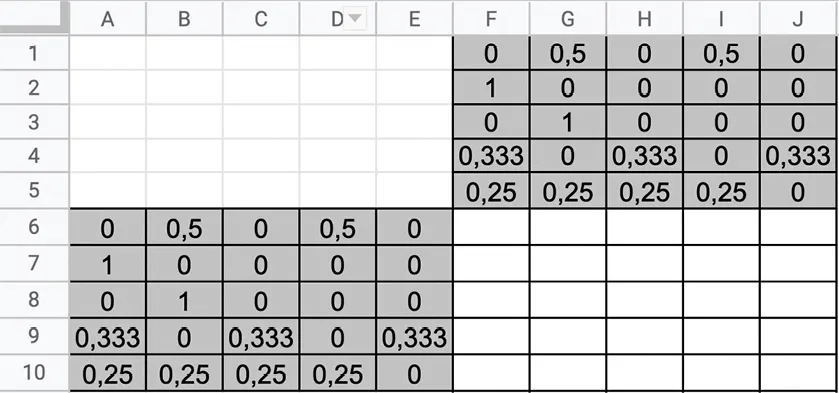
b. Quelle formule faut‑il écrire dans la cellule F6 et étirer sur la plage F6:J10 pour obtenir \mathrm{P}^2 ?
c. Compléter les cellules de la plage F11:J15 en s'inspirant du contenu des cellules de la plage F6:J10 afin d'obtenir \mathrm{P}^3.
Calculer ensuite \mathrm{P}^4 sur la plage F16:J20.
3. En déduire une estimation de la probabilité, au bout d'un temps très long, d'être sur chacun des sites.
4. Cette probabilité dépend‑elle du choix du site de départ ?
2. a. Recopier la feuille de calcul suivante.


b. Quelle formule faut‑il écrire dans la cellule F6 et étirer sur la plage F6:J10 pour obtenir \mathrm{P}^2 ?
c. Compléter les cellules de la plage F11:J15 en s'inspirant du contenu des cellules de la plage F6:J10 afin d'obtenir \mathrm{P}^3.
Calculer ensuite \mathrm{P}^4 sur la plage F16:J20.
3. En déduire une estimation de la probabilité, au bout d'un temps très long, d'être sur chacun des sites.
4. Cette probabilité dépend‑elle du choix du site de départ ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
Le programme suivant permet de déterminer les pondérations de chaque site.
1. Compléter la fonction promenade qui simule les 1 000 premières minutes de la navigation du surfeur.
2. Simuler, avec la fonction PR à compléter ci‑dessous, la navigation de 1 000 surfeurs, et en déduire une estimation de la probabilité d'être sur chacun des sites au bout d'un temps très long.
3. Modifier le programme pour vérifier que le choix du site initial ne modifie pas les probabilités obtenues dans la question précédente.
1. Compléter la fonction promenade qui simule les 1 000 premières minutes de la navigation du surfeur.
import random def promenade(): # Simule les 1000 premières minutes de la marche aléatoire et renvoie le sommet sur lequel est le surfeur à la fin. sommet = "a" for pas in range(...): alea = random.random() if sommet == "a": if alea < 0.5: sommet = "b" else: ... elif ... elif ... elif ... else: ... return sommet
2. Simuler, avec la fonction PR à compléter ci‑dessous, la navigation de 1 000 surfeurs, et en déduire une estimation de la probabilité d'être sur chacun des sites au bout d'un temps très long.
def PR(): effectifs = 5*[0] surfeurs = ... for k in ...: sommetfinal = promenade() if sommetfinal == "a": effectifs[0] = effectifs[0] + 1/surfeurs elif ... elif ... elif ... else: ... return effectifs
3. Modifier le programme pour vérifier que le choix du site initial ne modifie pas les probabilités obtenues dans la question précédente.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
