Pour une distribution initiale \pi_{0}=(0,5 \quad 0,5), quelle est la probabilité de chacun des états de la chaîne de Markov au bout de trois transitions ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Flash

Déterminer une matrice de transition associée à une chaîne de Markov pour laquelle la distribution (0{,}1 \quad 0{,}9) est invariante.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

[Raisonner.]
Dans cet exercice, a et b désignent deux nombres réels de l'intervalle ]0\,; 1[.
Montrer que l'état \left(\frac{b}{a+b} \quad \frac{a}{a+b}\right) est l'unique distribution invariante de la chaîne de Markov associée au graphe probabiliste suivant.

Maths expertes - chapitre 7 - Suites et matrices - exercice 65

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

66
[Calculer.]
Soient x et y deux nombres réels strictements positifs dont la somme est inférieure ou égale à 1.
Montrer que l'état \left(\frac{1}{3} \quad \frac{1}{3} \quad \frac{1}{3}\right) est l'unique distribution invariante du graphe probabiliste suivant.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

67
[Communiquer.]

Photographie d'une table de Noël élégante. Une assiette est décorée d'un serpentins rouge et or et d'une boule de Noël. Décor festif rouge et or.

Selon les années, Nadège passe Noël soit chez ses parents, soit chez la famille de son mari Victor.
En 2020, Nadège fête Noël chez la famille de Victor.
Pour les années suivantes, elle choisit où passer Noël selon la règle suivante :

lorsqu'elle a passé Noël chez ses parents, il y a une probabilité de 0{,}3 qu'elle fête encore Noël chez eux l'année suivante ;
lorsqu'elle passe Noël chez la famille de Victor, il y a une probabilité de 0{,}6 qu'elle fête Noël chez ses parents l'année suivante.

Quelle est la probabilité qu'elle passe Noël chez ses parents en 2035 ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Algo

[Modéliser.]

On considère le graphe probabiliste ci‑dessous.

Maths expertes - chapitre 7 - Suites et matrices - exercice 68

À l'aide d'un programme en Python simulant une marche aléatoire sur le graphe, conjecturer la distribution invariante de cette chaîne de Markov.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Tableur

[Modéliser.]
On considère, dans le plan muni d'un repère orthonormé (\mathrm{O}\,; \overrightarrow{i}\,, \overrightarrow{j}) la suite \left(\mathrm{A}_{n}\right) de points définie par \mathrm{A}_{0}(0\,; 0), \mathrm{A}_{1}(1\,; 0) puis, pour tout entier naturel non nul n, on construit \mathrm{A}_{n+1} en déplaçant \mathrm{A}_{n} de 1 vers la droite ou de 1 vers le haut selon la règle suivante :

si le déplacement de \mathrm{A}_{n-1} vers \mathrm{A}_{n} est vers le haut, alors le déplacement de \mathrm{A}_{n} vers \mathrm{A}_{n+1} le sera aussi avec une probabilité de 0{,}6. Sinon, le déplacement de \mathrm{A}_{n} vers \mathrm{A}_{n+1} est vers la droite ;
si le déplacement de \mathrm{A}_{n-1} vers \mathrm{A}_{n} est vers la droite, alors le déplacement de \mathrm{A}_{n} vers \mathrm{A}_{n+1} le sera aussi avec une probabilité de 0{,}7. Sinon, le déplacement de \mathrm{A}_{n} vers \mathrm{A}_{n+1} est vers le haut.

1. Modéliser la suite des coordonnées de \overrightarrow{\mathrm{A}_{n} \mathrm{A}_{n+1}} par une chaîne de Markov dont on donnera la représentation par un graphe probabiliste.

Cliquez pour accéder à une zone de dessin

2. a. Reproduire le tableur suivant.

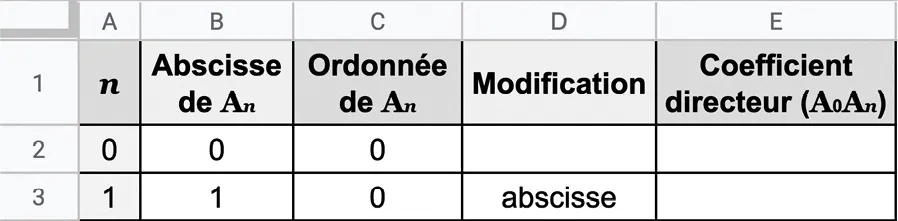
Tableau illustrant l'évolution d'une chaîne de Markov : abscisses, ordonnées et modifications successives sont indiquées.

b. Que doit‑on écrire dans la cellule D3 pour que le tableur écrive « abscisse » ou « ordonnée » selon la direction dans laquelle doit s'effectuer le déplacement de \mathrm{A}_1 ?

c. Compléter les cellules B4 et C4 pour déterminer les coordonnées de \mathrm{A}_2 en fonction de celles de \mathrm{A}_1 et du déplacement indiqué en D4.

d. Compléter la cellule E4 pour obtenir le coefficient directeur de la droite \left(\mathrm{A}_{0} \mathrm{A}_{2}\right).

3. Étirer la ligne 4 vers le bas pour calculer les coordonnées de \mathrm{A}_n pour tout n \leqslant 200 puis conjecturer la limite du coefficient directeur de \left(\mathrm{A}_{0} \mathrm{A}_{n}\right).

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

[Modéliser.]

Photo : formules mathématiques complexes sur fond bleu. Intégrales, racines carrées et équations sont visibles.

Ramanujan est un génie mathématique qui a trois activités au cours d'une journée : conjecturer de nouvelles formules mathématiques, démontrer des résultats et imaginer des applications aux résultats qu'il a déjà inventés.
Chaque heure, il peut changer, ou pas, d'activité.

S'il a conjecturé de nouvelles formules au cours de l'heure précédente, il continue avec une probabilité de 0{,}3 ou il les démontre avec une probabilité égale à 0{,}5 ;
s'il a démontré des résultats, il continue avec une probabilité de 0{,}05 ou il imagine des applications à ses résultats avec une probabilité 0{,}75 ;
s'il a imaginé des applications, il continue avec une probabilité de 0{,}5 ou il conjecture de nouvelles formules avec une probabilité égale à 0{,}2.

1. Représenter graphiquement la chaîne de Markov associée à la situation et déterminer la matrice de transition.

Cliquez pour accéder à une zone de dessin

2. Au début de la journée, Ramanujan commence toujours par conjecturer de nouvelles formules. Quelle est la probabilité que quatre heures plus tard, il soit en train de démontrer un résultat ?

3. Chaque jour, le mathématicien travaille 10 heures. Quelle est la probabilité qu'il s'occupe avec chacune de ces activités lors de sa dernière heure de travail ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

71
[Raisonner.]
On considère une chaîne de Markov à deux états \text{A} et \text{B} dans laquelle \mathrm{P}_{\mathrm{A}}(\mathrm{B})=\mathrm{P}_{\mathrm{B}}(\mathrm{A}) avec \mathrm{P}_{\mathrm{A}}(\mathrm{B}) différent de 0 et de 1.

1. Que peut‑on dire de la matrice de transition ?

2. Montrer qu'à long terme, quelle que soit la distribution de probabilité initiale, les deux états sont équiprobables.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

[Chercher.]a
On considère la chaîne de Markov définie par la matrice de transition \left(\begin{array}{cc}p(2-p) & (1-p)^{2} \\ p & 1-p\end{array}\right), avec p \in[0\,; 1], et par la distribution initiale (0,3 \quad 0,7).

1. Déterminer p pour que la deuxième composante de la distribution de probabilité soit maximale après une transition.

2. Que vaut alors la première composante de cette distribution de probabilité ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

73
[Modéliser.]
Dans un pays, les habitants peuvent soit être des citoyens, soit être des soldats, soit être des dirigeants. Chaque année :

un soldat peut devenir un citoyen avec une probabilité de 0{,}1. Sinon, il reste un soldat ;
un citoyen peut devenir un soldat avec une probabilité de 0{,}2, être élu dirigeant avec une probabilité de 0{,}3 ou rester un citoyen ;
un dirigeant peut se faire réélire avec une probabilité de 0{,}1. Il peut également devenir un soldat avec une probabilité de 0{,}6. Dans tous les autres cas, il devient citoyen.

1. Représenter cette situation par une chaîne de Markov (donnée sous la forme d'un graphe probabiliste).

Cliquez pour accéder à une zone de dessin

2. On choisit un citoyen. Quelle est la probabilité qu'il soit dirigeant dans deux ans ? Dans trois ans ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

74
SVT

[Modéliser.]

Photographie macro d'abeilles sur une ruche, rayons de miel.

Un essaim d'abeilles peut évoluer chaque année de trois manières qui s'excluent mutuellement. Il peut essaimer, produire du miel, ou contracter une maladie.
L'évolution suit les règles suivantes :

s'il a essaimé l'année passée, il contracte une maladie l'année en cours avec une probabilité de 0{,}1 et il produit du miel avec une probabilité de 0{,}8 ;
s'il a produit du miel l'année passée, il essaime avec une probabilité de 0{,}9 et il contracte une maladie avec une probabilité de 0{,}05 ;
s'il a contracté une maladie l'année passée, il en contracte une nouvelle l'année en cours avec une probabilité de 0{,}03 et il produit du miel avec une probabilité de 0{,}8.

La première année, un naturaliste observe que la ruche a essaimé.

1. Quelle est la probabilité qu'elle soit à nouveau en train d'essaimer lorsque le naturaliste reviendra trois années plus tard ?

2. Si on observe le développement de l'essaim sur une longue période, quelle proportion représentent les années où cet essaim a produit du miel ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

75
[Modéliser.]

Photographie d'un long couloir carcéral aux cellules alignées, barreaux jaunes, ambiance sombre.

Les Dalton sont en prison. Chaque semaine, ils tentent de s'évader. Leur tentative est une réussite dans 30 % des cas. Une fois évadés, la probabilité qu'ils se fassent capturer chaque semaine s'élève à 80 %.

1. Modéliser cette situation par une chaîne de Markov à deux états. On notera \text{L} l'état « les Dalton sont libre » et \text{P} l'état « les Dalton sont en prison ».

Cliquez pour accéder à une zone de dessin

2. Déterminer la probabilité qu'ils soient libres au bout de huit semaines.

3. Quelle est la probabilité qu'ils purgent la totalité de leur peine d'un mois de prison (quatre semaines) sans avoir réussi à s'évader une seule fois ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

[Chercher.]
1. Trouver deux nombres réels strictement positifs x et y solutions du système ci‑dessous, vérifiant x+y=1.

\left\{\begin{array}{l}\frac{2}{3} x+\frac{1}{6} y=x \\ \frac{1}{3} x+\frac{5}{6} y=y\end{array}\right..

2. En déduire une distribution invariante de la chaîne de Markov définie par la matrice de transition

\mathrm{P}=\left(\begin{array}{ll}\frac{2}{3} & \frac{1}{3} \\ \frac{1}{6} & \frac{5}{6}\end{array}\right).

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

[Chercher.]
On considère une chaîne de Markov \left(\mathrm{X}_{n}\right) ayant pour distribution invariante \pi. Soit \left(\mathrm{Z}_{n}\right) la chaîne de Markov définie, pour tout n \in \mathbb{N}, par \mathrm{Z}_{n}=\mathrm{X}_{2 n}.
Montrer que \pi est également une distribution invariante de \left(\mathrm{Z}_{n}\right).

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Démo

[Raisonner.]
Soit \left(\mathrm{X}_{n}\right) une chaîne de Markov à deux états numérotés 1 et 2 dont on note \text{P} la matrice de transition associée, les sommets étant rangés dans l'ordre croissants, et \pi_0 la distribution initiale.
On note, pour tout entier naturel n, \pi_n la matrice ligne correspondant à la distribution de probabilité de la variable aléatoire \mathrm{X}_{n}.

1. En revenant à la définition d'une chaîne de Markov \mathrm{X}_{n} et de \text{P}, justifier que, pour tout entier naturel n, \pi_{n+1}=\pi_{n} \mathrm{P}.

2. Montrer alors par récurrence sur n que \pi_{n}=\pi_{0} \mathrm{P}^{n}.

3. Reprendre cette démonstration dans le cadre d'une chaîne de Markov à 3 états.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.