Enseignement scientifique Terminale - 2024

Retourner à l'accueil
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Sciences, climat et société
Ouverture de thème
p. 12-14
Ch. 1
L’atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Se préparer à l'évaluation - Thème 1
Le futur des énergies
Ouverture de thème
p. 83
Ch. 4
Deux siècles d’énergie électrique
Ch. 5
Conversion et transport de l’énergie électrique
Ch. 6
Énergie, développement et futur climatique
Se préparer à l'évaluation - Thème 2
Une histoire du vivant
Une histoire du vivant
Ouverture de thème p. 152-154
Ch. 7
La biodiversité et son évolution
Ch. 8
L’évolution comme grille de lecture du monde
Ch. 9
L’évolution humaine
Ch. 10
Les modèles démographiques
Ch. 11
De l’informatique à l’intelligence artificielle
Se préparer à l'évaluation - Thème 3
Livret maths
Calcul littéral
Livret mathsp. 262-264
Conversions
Livret mathsp. 262
Informations chiffrées
Livret mathsp. 266
Intervalles de confiance et fluctuation d’échantillonnage
Livret mathsp. 267
Probabilités conditionnelles
Livret mathsp. 268
Suites arithmétiques et géométriques
Livret mathsp. 269
Droites et fonctions affines
Livret mathsp. 270-271
Régression linéaire
Livret mathsp. 272
Étude de graphiques complexes
Livret mathsp. 273
Calculs d’aires et de volumes
Livret mathsp. 274
Fiches méthode
Esprit critique et scientifique
Améliorer ses compétences
Fiches histoire
Annexes
Livret maths 1

Calcul littéral

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours 1

Objectif
Je veux revoir le calcul fractionnaire

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Soient a, b, c et d quatre nombres réels, avec b et d non nuls.

  • Somme et différence de fractions

    Pour calculer la somme ou la différence de deux fractions, on commence systématiquement par réduire ces fractions au même dénominateur :
    • \frac{a}{b}+\frac{c}{d}=\frac{a \times d}{b \times d}+\frac{c \times b}{d \times b}=\frac{a d+c b}{b d} \text {; }

    • \frac{a}{b}-\frac{c}{d}=\frac{a \times d}{b \times d}-\frac{c \times b}{d \times b}=\frac{a d-c b}{b d}.
    Remarque
    On peut écrire \frac{a+c}{b}=\frac{a}{b}+\frac{c}{b}. Cependant, \frac{a}{b+d} n'admet pas de décomposition dans le cas général.

  • Produit et quotient de fractions

    On a \frac{a}{b} \times \frac{c}{d}=\frac{a c}{b d}. Il est donc inutile de réduire les deux fractions au même dénominateur.
    On rappelle que diviser par un nombre équivaut à multiplier par son inverse. Ainsi, dans le cas où c est également non nul :
    \frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a}{b} \times \frac{d}{c}=\frac{a d}{b c}.
    • Remarque
    Prendre une fraction d'une quantité, c'est multiplier la quantité par cette fraction.

  • Fractions et pourcentages

    Un pourcentage est une fraction dont le dénominateur vaut 100.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
1
On considère trois nombres réels non nuls \mathrm{R}_1, \mathrm{R}_2 et \mathrm{R}_3. Écrire sous la forme d'une seule fraction la quantité \frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
2
On estime que 71 % de la Terre est occupée par les océans. On estime également la surface terrestre à 510 millions de kilomètres carrés. Quelle est la surface sur Terre occupée par les océans ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours 2

Objectif
Je veux revoir la proportionnalité

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Deux grandeurs sont dites proportionnelles lorsque les valeurs de l'une peuvent être obtenues en multipliant les valeurs de l'autre par un même nombre non nul k appelé coefficient de proportionnalité.
Lorsqu'on connaît trois valeurs d'un tableau de proportionnalité, on peut déterminer la quatrième.

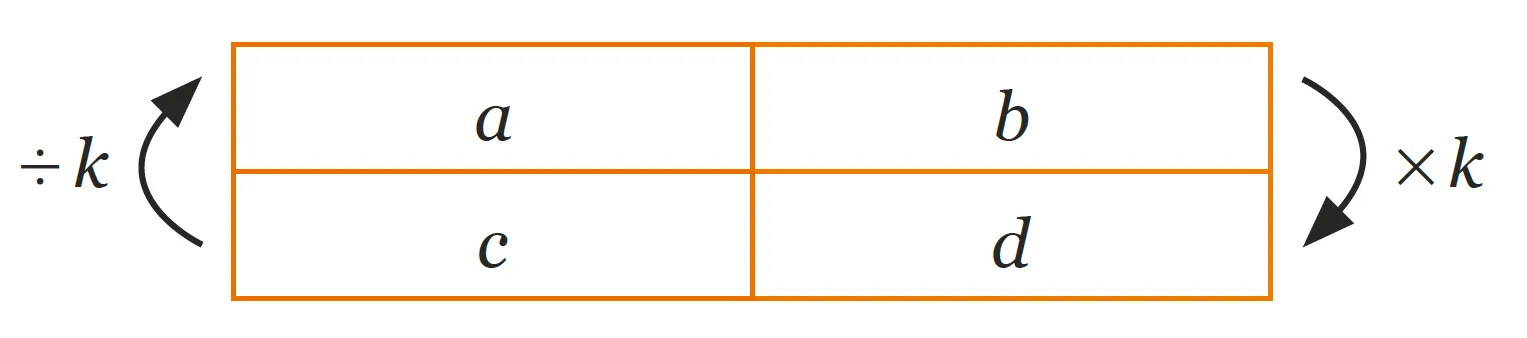
Placeholder pour Tableau de proportionnalitéTableau de proportionnalité

On a a=\frac{b \times c}{d}, b=\frac{a \times d}{c}, c=\frac{a \times d}{b} et d=\frac{b \times c}{a}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Question

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
3
Pour estimer l'abondance \mathrm{N} d'une population dans un milieu, la méthode de capture-marquage-recapture consiste à prélever \mathrm{M} individus, à les marquer, puis à les relâcher.
Dès lors, la proportion d'individus marqués dans la population est \frac{\mathrm{M}}{\mathrm{N}}.
On procède à une deuxième capture de n individus et on observe que, parmi eux, m sont marqués.
On peut supposer que la proportion d'individus marqués ne varie pas selon l'échantillon de population choisi.

a. Expliquer comment on peut estimer la valeur \mathrm{N} du nombre total d'individus dans cette population.
b. On suppose qu'on a procédé au marquage de 1 827 poissons d'une rivière qu'on a ensuite relâchés. Lors de la seconde capture, on pêche 1 337 poissons dont 423 sont marqués. À combien peut-on estimer le nombre de poissons dans cette rivière ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours 3

Objectif
Je veux revoir les règles de calcul sur les racines carrées et les puissances

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

  • Racines carrées

    Soient a un nombre positif ou nul et b un nombre strictement positif.
    On a \sqrt{a \times b}=\sqrt{a} \times \sqrt{b} et \sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}.
    Remarque
    Il n'y a pas d'égalité similaire pour les additions ou les soustractions.
    Il faut également faire attention : dans le cas général, \sqrt{a^2}=|a|.

  • Puissances

    Soient a un nombre réel non nul, et m et n deux entiers. On a les règles de calcul suivantes.

    1. a^{m+n}=a^m \times a^n

    2. \frac{1}{a^n}=a^{-n}
    3. \frac{a^m}{a^n}=a^{m-n}

    4. \left(a^m\right)^n=a^{m \times n}

    Remarque
    2 \times 4^n ne vaut pas 8^n. En revanche, 2 \times 4^n=2 \times\left(2^2\right)^n=2 \times 2^{2 n}=2^{1+2 n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
4
Calculer, sans calculatrice, la valeur exacte des quantités suivantes sous la forme la plus simple possible.

\mathrm{A}=\sqrt{20}-2 \sqrt{45}
\mathrm{B}=\sqrt{300}-4 \sqrt{27}
\mathrm{C}=2 \sqrt{100}+3 \sqrt{9}
\mathrm{D}=5 \sqrt{12}-3 \sqrt{27}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
5
Écrire les nombres suivants sous la forme d'une puissance de 10.

\mathrm{E}=10 000 000 000
\mathrm{F}=1 000 000 \times 0,00001
\mathrm{G}=\frac{10 000 \times 0,0000001}{0,00001 \times 0,00001}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
6
Calculer, en utilisant les puissances de 10, les quantités suivantes.

\mathrm{H}=\left(10^{-9}\right)^3 \times\left(10^3\right)^9
\mathrm{K}=\frac{1 000 \times 10^{-5}}{10^{-3} \times 10^2}
\mathrm{L}=\frac{10^{-5} \times 10^{-3} \times 10^{11}}{0,00001 \times 10^7}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
7
Écrire chacune des quantités suivantes sous la forme d'une seule puissance (m et n sont deux entiers).

\mathrm{M}=8 \times 2^m \times 4^n
\mathrm{N}=\frac{25^m}{5^n}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours 4

Objectif
Je veux utiliser l'écriture scientifique d'un nombre décimal

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
  • Une puissance de 10 est un nombre décimal pouvant s'écrire sous la forme 10^n où n est un entier (éventuellement négatif).
  • Tout nombre décimal non nul peut s'écrire, de manière unique, sous la forme \pm a \times 10^n, où a est un nombre décimal vérifiant 1 \leqslant a\lt10 et n un entier relatif. On dit alors que le nombre est écrit sous forme d'écriture scientifique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemple

  • 578=5,78 \times 10^2
  • 3=3\times 10^0
  • 0,25=2,5 \times 10^{-1}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
L'écriture scientifique est particulièrement adaptée à la comparaison de nombres décimaux. Pour comparer deux nombres écrits sous forme scientifique :
  • on compare leur puissance de 10 ;
  • si les puissances de 10 sont les mêmes, on compare le nombre a correspondant à la notation scientifique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
8
On donne ci-dessous les masses des huit planètes du Système solaire.

PlanèteMercureVénusTerreMarsJupiterSaturneUranusNeptune
Masse (kg)0,329 \times 10^{24}48,7 \times 10^{23}5,97 \times 10^{24}639 \times 10^{21}1,90 \times 10^{27}568 \times 10^{24}8,68 \times 10^{25}1,02 \times 10^{26}

a. Écrire les différentes masses sous forme d'écriture scientifique.
b. Classer les planètes du Système solaire dans l'ordre croissant de masse.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours 5

Objectif
Je veux revoir les règles de développement

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

  • Développement et factorisation

    On considère quatre réels a, b, c et d. On a :
    • a(b+c)=a b+a c
    • (a+b)(c+d)=a c+a d+b c+b d

  • Identités remarquables

    Soient a et b deux réels. On a :
    • (a+b)^2=a^2+2 a b+b^2
    • (a-b)^2=a^2-2 a b+b^2
    • (a+b)(a-b)=a^2-b^2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
9
Développer chacune des expressions suivantes, toutes les données étant des réels.

a. \mathrm{E}_{\mathrm{pp}}=m g\left(z_{\mathrm{A}}-z_{\mathrm{B}}\right)
b. v^2=\left(v_1-v_2\right)^2
c. \mathrm{L}=(2 \mathrm{H}-h)^2
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours 6

Objectif
Je veux isoler une grandeur dans une égalité

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Pour isoler une grandeur qui n'apparaît qu'une fois dans une égalité, il faut, dans un premier temps, lister toutes les opérations la mettant en jeu en prenant garde aux priorités opératoires. Ensuite, on remonte cette liste d'opérations en les inversant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exemple

On veut isoler v dans l'égalité \mathrm{E}_c=\frac{1}{2} m v^2. On observe que v est élevé au carré, puis multiplié par m et par \frac{1}{2}.
Pour l'isoler, on commence par diviser par \frac{1}{2}, c'est-à-dire multiplier par 2 : 2 \mathrm{E}_c=m v^2, puis on divise par m : \frac{2 \mathrm{E}_c}{m}=v^2. En utilisant la racine carrée et puisque v est positif, on obtient v=\sqrt{\frac{2 \mathrm{E}_c}{m}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Question

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
10
Pour chacune des égalités suivantes, isoler le paramètre indiqué. a. Isoler d dans \mathrm{F}=\frac{\mathrm{Gmm'}}{d^2} sachant que d est strictement positif.
b. Isoler \mathrm{T} dans \mathrm{R}=\mathrm{R}_0(1+a \mathrm{~T}) sachant que \mathrm{R}_0 et a sont non nuls.
c. Isoler \mathrm{T} dans \frac{\mathrm{T}^2}{a^3}=\mathrm{C} sachant que \mathrm{T} est positif.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours 7

Objectif
Je veux résoudre des équations

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Résoudre une équation, c'est trouver toutes les valeurs de l'inconnue pour lesquelles l'égalité est vraie.

  • Résolution d'équations du premier degré

    Une équation du premier degré est une équation pouvant s'écrire sous la forme a x+b=c x+d, où a, b, c et d sont quatre nombres réels fixés.
    On résout ces équations en manipulant les égalités de manière à isoler l'inconnue.

  • Résolution d'équations au produit nul

    Une équation au produit nul est une équation de la forme \mathrm{A}(x) \times \mathrm{B}(x)=0.
    Pour résoudre cette équation, on utilise la propriété suivante : un produit de réels est nul si, et seulement si, un de ses facteurs est nul.
    Autrement dit, \mathrm{A}(x) \times \mathrm{B}(x)=0 signifie que soit \mathrm{A}(x)=0, soit \mathrm{B}(x)=0. On résout ensuite ces équations séparément.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Question

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
11
Résoudre dans \mathbb{R} les équations suivantes.
a. 4 x-5=7 x-8
b. 3 x+5=-2 x+4
c. (5 x+1)(-2 x+3)=0
d. (2 x-1)(7 x+3)(-2 x-4)=0
e. x^2-4=0
Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.