Une suite u est arithmétique lorsqu'il existe un nombre réel r appelé raison de la suite arithmétique tel que, pour tout entier naturel n, u(n+1)=u(n)+r. Dans ce cas, pour tout entier naturel n, u(n)=u(0)+n r.
Dans la pratique, ces suites sont utilisées pour modéliser des situations dans lesquelles la variation absolue de la grandeur considérée entre deux instants consécutifs est constante. Dans les faits, on s'autorise à utiliser un modèle de suite arithmétique pour représenter une situation dans laquelle la variation absolue de la grandeur considérée entre deux instants consécutifs est quasi constante.
Graphiquement, la modélisation d'une évolution par une suite arithmétique met en évidence le caractère linéaire de l'évolution.

Une suite u est géométrique lorsqu'il existe un nombre réel q appelé raison de la suite géométrique tel que, pour tout entier naturel n, u(n+1)=q \times u(n). Dans ce cas, pour tout entier naturel n, u(n)=u(0) \times q^n.
Dans la pratique, ces suites sont utilisées pour modéliser des situations dans lesquelles la variation relative de la grandeur considérée entre deux instants consécutifs est constante.
Dans les faits, on s'autorise à utiliser un modèle de suite géométrique pour représenter une situation dans laquelle la variation relative de la grandeur considérée entre deux instants consécutifs est quasi constante.
Graphiquement, la modélisation d'une évolution par une suite géométrique met en évidence le caractère exponentiel de l'évolution.

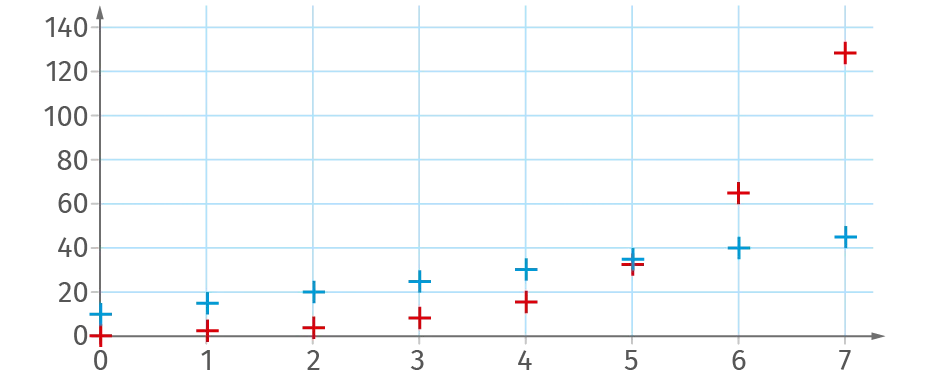
On a représenté ci-contre deux suites. La suite correspondant aux points bleus est la suite arithmétique de raison r=5 et de premier terme u(0)=10. Les points de ce nuage sont alignés (évolution linéaire). La suite correspondant aux points rouges est la suite géométrique de raison q=2 et de premier terme v(0)=1. Ce nuage de points souligne une évolution exponentielle.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Un médicament est prescrit pendant 10 semaines sous forme d'injections qui doivent être administrées une fois par semaine.
Chaque semaine, la quantité de médicament à injecter au patient est indiquée dans le tableau ci-dessous.

Numéro de l'injection	1	2	3	4	5	6
Quantité injectée (mL)	120	126	132,3	138,9	145,9	153,2

a. Placer ces données dans un repère.

Cliquez ici pour avoir accès à un espace de dessin

b. Proposer une suite arithmétique permettant de modéliser la quantité de médicament administrée à chaque injection.

c. En utilisant le modèle, quelle sera la dose de médicament injectée au patient au cours de la dernière injection ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Au moment de la fécondation, un embryon n'est composé que d'une seule cellule. Puis, on estime que chaque jour, durant les premiers jours, les cellules embryonnaires se divisent en deux. On note u(n) le nombre de cellules composant l'embryon au bout de n jours.

a. Déterminer la valeur u(0).

b. Calculer le nombre de cellules composant l'embryon au bout d'un jour, puis au bout de deux jours.

c. Compléter l'égalité suivante : pour tout entier naturel n, u(n+1)=

.

d. La suite u est-elle arithmétique ou géométrique ?

e. Chez les femmes, une grossesse dure environ 40 semaines. Estimer, en utilisant le modèle choisi, le nombre de cellules composant le foetus au terme de ces 40 semaines. Comparer la valeur trouvée au nombre total d'atomes estimés dans l'univers (environ 10⁸⁰). Le modèle étudié est-il réaliste ?

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Enseignement scientifique Terminale - 2024

Suites arithmétiques et géométriques

Point de cours

ObjectifJe veux revoir les généralités sur les suites arithmétiques et géométriques

Questions

Une erreur sur la page ? Une idée à proposer ?

Objectif
Je veux revoir les généralités sur les suites arithmétiques et géométriques