Enseignement scientifique Terminale - 2024
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Sciences, climat et société
Ch. 1
L’atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Se préparer à l'évaluation - Thème 1
Le futur des énergies
Ch. 4
Deux siècles d’énergie électrique
Ch. 5
Conversion et transport de l’énergie électrique
Ch. 6
Énergie, développement et futur climatique
Se préparer à l'évaluation - Thème 2
Une histoire du vivant
Ch. 7
La biodiversité et son évolution
Ch. 8
L’évolution comme grille de lecture du monde
Ch. 9
L’évolution humaine
Ch. 10
Les modèles démographiques
Ch. 11
De l’informatique à l’intelligence artificielle
Se préparer à l'évaluation - Thème 3
Livret maths
Fiches méthode
Esprit critique et scientifique
Améliorer ses compétences
Fiches histoire
Annexes
Livret maths 7
Droites et fonctions affines
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Point de cours
ObjectifJe veux lire un taux d'accroissement sur un graphique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définitions
Une fonction f définie sur \mathbb{R} est une fonction affine lorsqu'il existe deux réels m et p tels que, pour tout
réel x, f(x)=m x+p.
Dans le cas particulier où p = 0, on dit que la fonction f est linéaire.
Dans le cas particulier où p = 0, on dit que la fonction f est linéaire.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
- Lors de l'étude des transferts thermiques, on met en évidence que, sous certaines hypothèses, la répartition de température \mathrm{T}(x) au point d'abscisse x à travers un mur peut s'écrire sous la forme \mathrm{T}(x)=m x+p.
- Lors de l'étude d'un circuit électrique uniquement composé d'un générateur de courant et d'une résistance, la tension \mathrm{U}, en volt (\mathrm{V}), aux bornes de la résistance \mathrm{R}, en ohm (\Omega), ne dépend que de l'intensité du courant \mathrm{I}, en ampère (\mathrm{A}), traversant la résistance. La tension \mathrm{U} est une fonction linéaire de \mathrm{I} qui vérifie \mathrm{U}(\mathrm{I})=\mathrm{R} \times \mathrm{I}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour trouver une expression algébrique d'une fonction affine pour laquelle la représentation graphique est
donnée, on utilise le taux d'accroissement de la droite (aussi appelé coefficient directeur ou pente) qui mesure
l'inclinaison de la droite et qui correspond à la valeur de m. La valeur de p correspond à l'ordonnée à l'origine,
c'est-à-dire l'intersection de la droite avec l'axe des ordonnées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
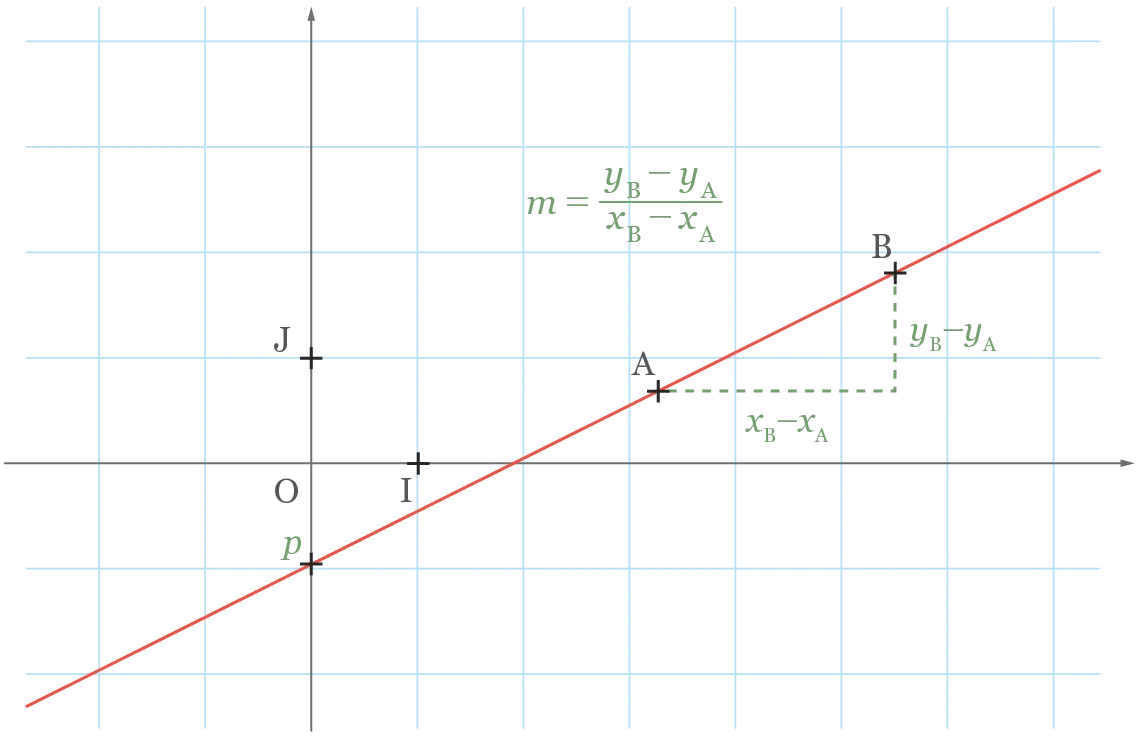
Propriété
Pour calculer le taux d'accroissement d'une droite, on choisit deux points \mathrm{A}\left(x_{\mathrm{A}} ; y_{\mathrm{A}}\right) et \mathrm{B}\left(x_{\mathrm{B}} ; y_{\mathrm{B}}\right) distincts
appartenant à la droite. On a :
Lorsque le taux d'accroissement de la droite est positif, la droite est orientée vers le haut et lorsque le taux d'accroissement est négatif, la droite est orientée vers le bas.
m=\frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{x_{\mathrm{B}}-x_{\mathrm{A}}}
Lorsque le taux d'accroissement de la droite est positif, la droite est orientée vers le haut et lorsque le taux d'accroissement est négatif, la droite est orientée vers le bas.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans le cas particulier où \mathrm{A} et \mathrm{B} sont deux points de la droite tels que x_{\mathrm{B}}-x_{\mathrm{A}}=1, on a :
m=\frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{1}=y_{\mathrm{B}}-y_{\mathrm{A}}.
m=\frac{y_{\mathrm{B}}-y_{\mathrm{A}}}{1}=y_{\mathrm{B}}-y_{\mathrm{A}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
La fonction affine f représentée ci-dessous permet
de convertir une température, exprimée en degré
Celcius (°C), en degré Fahrenheit (°F).

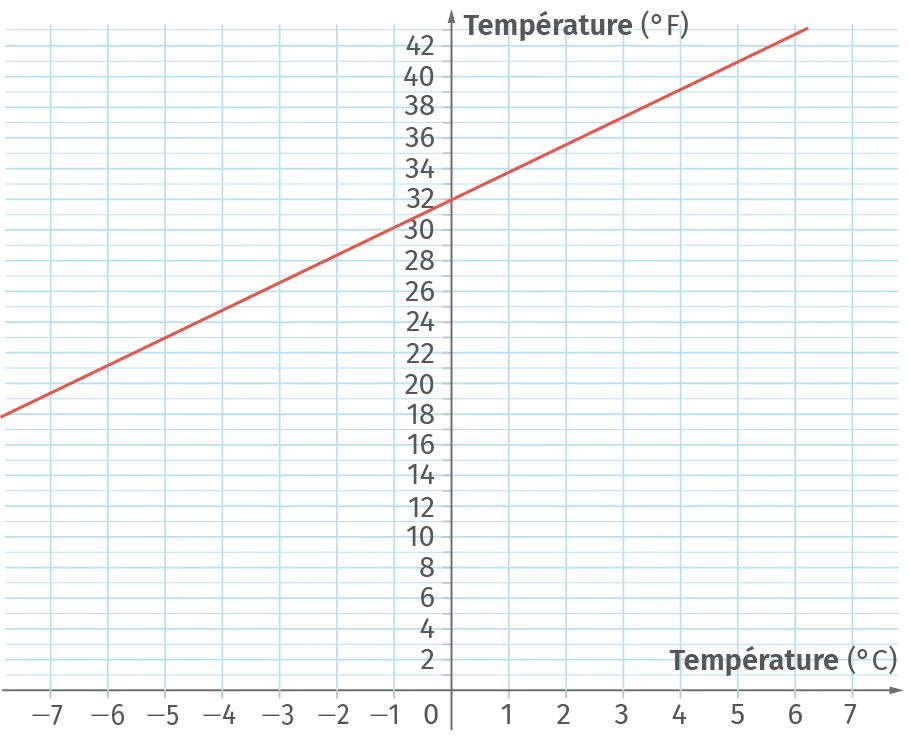
a. À l'aide du graphique, proposer une expression de la fonction f.
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Le modèle de White permet d'exprimer la
température moyenne \mathrm{T} à la surface de la Terre, en
degrés Celcius (°C), en fonction de la concentration en
dioxyde de carbone CO2, notée c et exprimée en partie
par million (ppm), dans l'atmosphère.Le graphique ci-dessous permet de mettre en évidence la dépendance entre cette température et la concentration moyenne de dioxyde de carbone CO2.

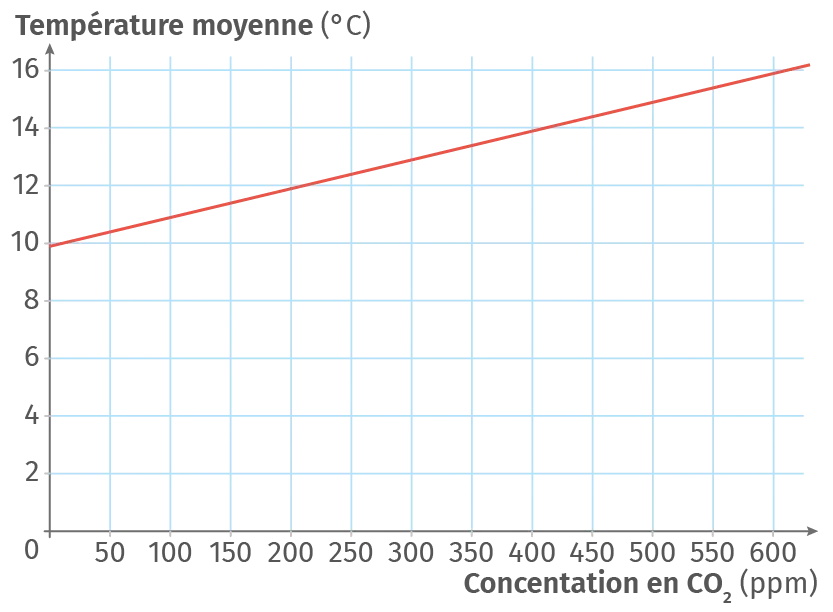
a. Justifier que la courbe représente une fonction affine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
On considère le mur d'une maison d'épaisseur e
séparant deux milieux. L'intérieur de la maison est à
une température \mathrm{T}_1 et l'extérieur de la maison à une
température \mathrm{T}_2. On suppose que \mathrm{T}_1 > \mathrm{T}_2.On souhaite déterminer la température T à travers le mur.
On note x=0 l'abscisse correspondant à la paroi intérieure et x=e l'abscisse correspondant à la paroi extérieure.
On peut montrer que sous certaines conditions, la température du mur à l'abscisse x \in[0 ; e] est donnée par :
\mathrm{T}(x)=\mathrm{T}_1+\frac{x}{e}\left(\mathrm{~T}_2-\mathrm{T}_1\right)
a. Quel est le coefficient directeur de la droite associée à la fonction affine \mathrm{T} ? Quel est son signe ? Que peut-on en déduire ?
Cliquez ici pour avoir accès à un espace de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
La méthode de datation au rubidium-strontium
est une méthode de datation permettant notamment
de déterminer l'âge de certains récifs montagneux.Cette méthode repose sur l'observation d'un élément radioactif, le rubidium 87 (87Rb), qui se désintègre en strontium 87 (87Sr). Plus précisément, on procède à différentes mesures des rapports 87Sr/86Sr et 87Rb/86Sr sur différents échantillons du minéral étudié.
En positionnant les mesures obtenues dans un repère, on peut tracer une droite approchant le nuage de points et dont le coefficient directeur permet de déterminer l'âge du minéral.

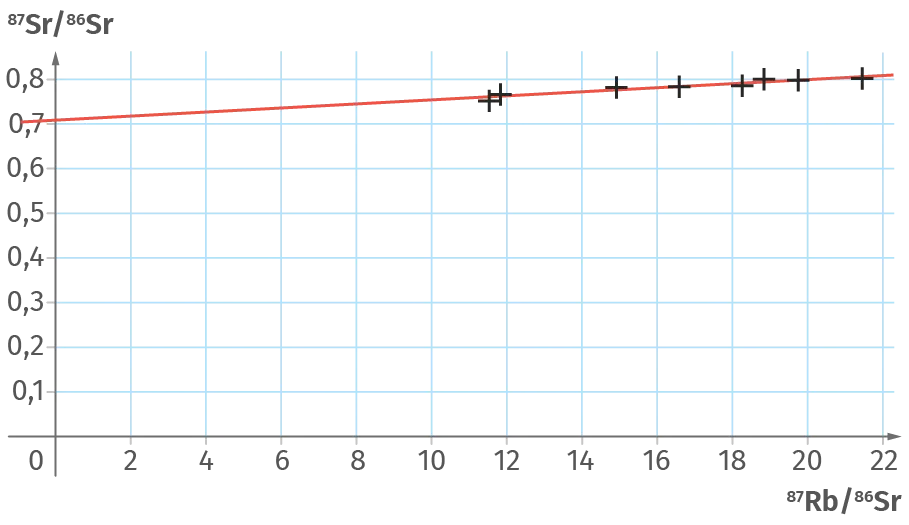
a. Déterminer le coefficient directeur de la droite tracée ci-dessus.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
