Enseignement scientifique Terminale - 2024
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Sciences, climat et société
Ch. 1
L’atmosphère terrestre et la vie
Ch. 2
La complexité du système climatique
Ch. 3
Le climat du futur
Se préparer à l'évaluation - Thème 1
Le futur des énergies
Ch. 4
Deux siècles d’énergie électrique
Ch. 5
Conversion et transport de l’énergie électrique
Ch. 6
Énergie, développement et futur climatique
Se préparer à l'évaluation - Thème 2
Une histoire du vivant
Ch. 7
La biodiversité et son évolution
Ch. 8
L’évolution comme grille de lecture du monde
Ch. 9
L’évolution humaine
Ch. 10
Les modèles démographiques
Ch. 11
De l’informatique à l’intelligence artificielle
Se préparer à l'évaluation - Thème 3
Livret maths
Fiches méthode
Esprit critique et scientifique
Améliorer ses compétences
Fiches histoire
Annexes
Livret maths 5
Probabilités conditionnelles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Point de cours
ObjectifJe veux revoir les probabilités conditionnelles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
On considère une expérience aléatoire pour laquelle on étudie deux événements A et B.

Lorsque \mathrm{P}(\mathrm{A}) \neq 0, on appelle probabilité de \mathrm{B} sachant \mathrm{A}, notée \mathrm{P}_{\mathrm{A}}(\mathrm{B}), la probabilité
que l'évènement \mathrm{B} se produise lorsque l'évènement \mathrm{A} s'est déjà produit.
On a \mathrm{P}_{\mathrm{A}}(\mathrm{B})=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}.
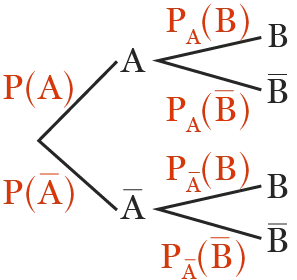
Sur un arbre de probabilités, la situation se représente de la façon ci-contre.
On a \mathrm{P}_{\mathrm{A}}(\mathrm{B})=\frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{A})}.
Sur un arbre de probabilités, la situation se représente de la façon ci-contre.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
On peut utiliser cet arbre de probabilités pour calculer \mathrm{P}(\mathrm{B}) :
\mathrm{P}(\mathrm{B})=\mathrm{P}(\mathrm{A} \cap \mathrm{B})+\mathrm{P}(\overline{\mathrm{A}} \cap \mathrm{B})
Par ailleurs, si \mathrm{P}(\mathrm{B}) ≠ 0, \mathrm{P}B(A)= \frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}.
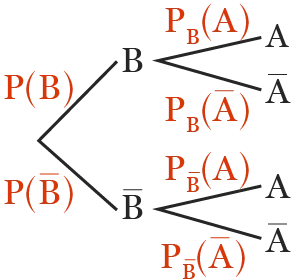
Ces deux formules permettent « d'inverser » l'arbre de probabilités pour obtenir l'arbre ci-contre.
\mathrm{P}(\mathrm{B})=\mathrm{P}(\mathrm{A} \cap \mathrm{B})+\mathrm{P}(\overline{\mathrm{A}} \cap \mathrm{B})
Par ailleurs, si \mathrm{P}(\mathrm{B}) ≠ 0, \mathrm{P}B(A)= \frac{\mathrm{P}(\mathrm{A} \cap \mathrm{B})}{\mathrm{P}(\mathrm{B})}.
Ces deux formules permettent « d'inverser » l'arbre de probabilités pour obtenir l'arbre ci-contre.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il ne faut pas confondre \mathrm{P}(\mathrm{A} \cap \mathrm{B}) et \mathrm{P}_{\mathrm{A}}(\mathrm{B}). En effet :
- \mathrm{P}(\mathrm{A} \cap \mathrm{B}) correspond à la probabilité que les évènements \mathrm{A} et \mathrm{B} se produisent simultanément en prenant en considération toutes les issues possibles de l'expérience ;
- \mathrm{P}_{\mathrm{A}}(\mathrm{B}) correspond à la probabilité que l'évènement \mathrm{B} se produise lorsqu'on sait que \mathrm{A} s'est déjà produit. On ne travaille dès lors plus à partir de toutes les issues possibles de l'expérience mais uniquement avec celles favorables à l'évènement \mathrm{A}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Lors de la mise au point d'un vaccin, on procède
à différents essais thérapeutiques sur un groupe de
patients volontaires. Il a été observé que 30 % d'entre
eux ont été malades. Parmi les patients malades, 1 sur
15 a été vacciné contre la maladie, un placebo ayant été
administré aux autres patients. Enfin, parmi les patients
n'ayant pas contracté la maladie, on compte deux
personnes ayant reçu le placebo pour une personne
ayant réellement été vaccinée.
On note :
- \mathrm{M} l'évènement : « Le patient a contracté la maladie » ;
- \mathrm{V} l'évènement : « Le patient a été vacciné contre la maladie ».
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Pour lutter contre la résistance bactérienne, des
tests rapides ont été mis à disposition des médecins
pour déterminer si une angine est d'origine bactérienne
ou virale. Ce test est positif lorsque le patient est atteint
d'une angine bactérienne, ce qui arrive uniquement
dans 15 % des cas. On dispose des informations
suivantes sur ces tests :
- la probabilité que le test soit positif sachant que le sujet est réellement atteint d'une angine bactérienne est de 90 % ;
- parmi les sujets non atteints d'une angine bactérienne, la probabilité que le test soit négatif est de 95 %.
a. Construire un arbre de probabilités permettant de représenter la situation.
Cliquez ici pour avoir accès à un espace de dessin
b. On choisit un patient au hasard. Quelle est la probabilité que le sujet ait un test bactérien positif ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
