1. Le théorème de Thalès

1. Dans la figure, justifier que les droites (\text{IN}) et (\text{AO}) sont parallèles.

2. On donne \mathrm{PA}=38 \mathrm{~cm}, \mathrm{IA}=28,5 \mathrm{~cm} et \mathrm{IN}=7 \mathrm{~cm}. Déterminer les longueurs \text{PI} puis \text{AO}.

42

[Mod.4 - Mod.5 - Rais.3]

Paul tient une règle verticalement et tend son bras en direction d'une grue parfaitement verticale dont il désire connaître la hauteur. On modélise la situation par le schéma suivant, où \mathrm{S} désigne l'œil de Paul, [\text{AL}] désigne sa règle et [\text{UE}] est la grue. Les points \text{S}, \text{A} et \text{U} sont alignés, ainsi que les points \mathrm{S}, \mathrm{L} et \mathrm{E}.

44

[Mod.4 - Rais.4]

D'après Brevet, Nouvelle-Calédonie, 2013
En se retournant lors d'une marche arrière, le conducteur d'une camionnette voit le sol à 6 mètres derrière son camion. Sur le schéma, la zone grisée correspond à ce que le conducteur ne voit pas lorsqu'il regarde en arrière.

D'après Brevet, Nouvelle-Calédonie, 2020
En lien avec le théorème de Pythagore.
Thomas attache son cerf-volant au sol au point \mathrm{T}. Il fait \text{20} pas pour parcourir la distance \text{TH}. Un pas mesure \text{0,6} mètre. Le schéma illustre la situation. Il n'est pas à l'échelle.

1. Montrer que la hauteur \mathrm{CH} du cerf-volant est égale à 9 \mathrm{~m}.

2. Thomas souhaite que son cerf-volant atteigne une hauteur de 13,5 \mathrm{~m}. Calculer la longueur \text{TE} de la corde nécessaire.

46

[Ch.1 - Ch.2 - Rep.6 - Rais.2]

Lors d'une éclipse totale de Soleil, le centre de la Terre, le centre de la Lune et le centre du Soleil sont supposés alignés. On sait que la distance Terre-Lune est égale à 384~400 \mathrm{~km}, que le rayon de la Lune est égal à 1~737 \mathrm{~km} et que celui du Soleil mesure 696~340 \text{~km}.
Sachant que le disque lunaire recouvre exactement le disque solaire, calculer la distance Terre-Soleil au moment de cette éclipse.

47

[Ch.2 - Com.4 - Rais.4]

La piscine d'un centre de vacances a construit un nouveau plongeoir. On sait que \mathrm{BD}=1,5 \mathrm{~m}, \mathrm{BA}=4 \mathrm{~m}, \mathrm{BE}=1,9 \mathrm{~m} et \mathrm{BC}=5 \mathrm{~m}.
Montrer que ce plongeoir n'est pas parallèle à la surface de l'eau.

48

[Ch.2 - Rais.2 - Com.4]

Une croix de bûcheron est un outil en forme de T, symbolisé dans la figure ci-dessous par les deux segments \text{[OB]} et \text{[AC]} perpendiculaires et de même longueur. Le point \text{O} représente l'œil d'un observateur. L'observateur place la croix de bûcheron devant son œil de manière à recouvrir exactement la hauteur d'un arbre avec le segment \text{[AC]} tout en ayant la droite (\mathrm{OB}) parallèle au sol.

Dans la figure ci-dessous, on sait que (\text{IO}) et (\text{FN}) sont parallèles et que toutes les longueurs sont données en centimètres.

1. Démontrer que la droite \text{(IA)} n'est pas parallèle à la droite \text{(BN)}.

2. Le quadrilatère \text{FIOA} est-il un parallélogramme ?

Le professeur de Bastien donne l'exercice suivant.
\mathrm{ABC} est un triangle tel que \mathrm{AB}=12 \mathrm{~cm}, \mathrm{BC}=7,5 \mathrm{~cm} et \mathrm{AC}=16 \mathrm{~cm}.
\text{M} est un point de \text{[AB]} tel que \text{AM}=8 \mathrm{~cm} et \mathrm{N} est un point de [\mathrm{AC}] tel que \mathrm{AN}=10 \mathrm{~cm}.
De plus, on sait que \text{MN}=5 \mathrm{~cm}.

Quelle erreur a-t-il commise ? Corriger sa copie.

51

[Rais.4 - Com.4]

Pour vérifier une construction, un maçon plante un bâton de 60 \mathrm{~cm} perpendiculairement au sol, à 30 \mathrm{~m} du mur d'une maison qu'il vient de construire. Il sait que le mur de la maison mesure 10 \mathrm{~m} de hauteur et qu'en se positionnant à 2 \mathrm{~m} du bâton, alors les points \mathrm{A}, \mathrm{T} et \mathrm{S} sont alignés.

Démontrer que le mur de la maison n'est pas perpendiculaire au sol.

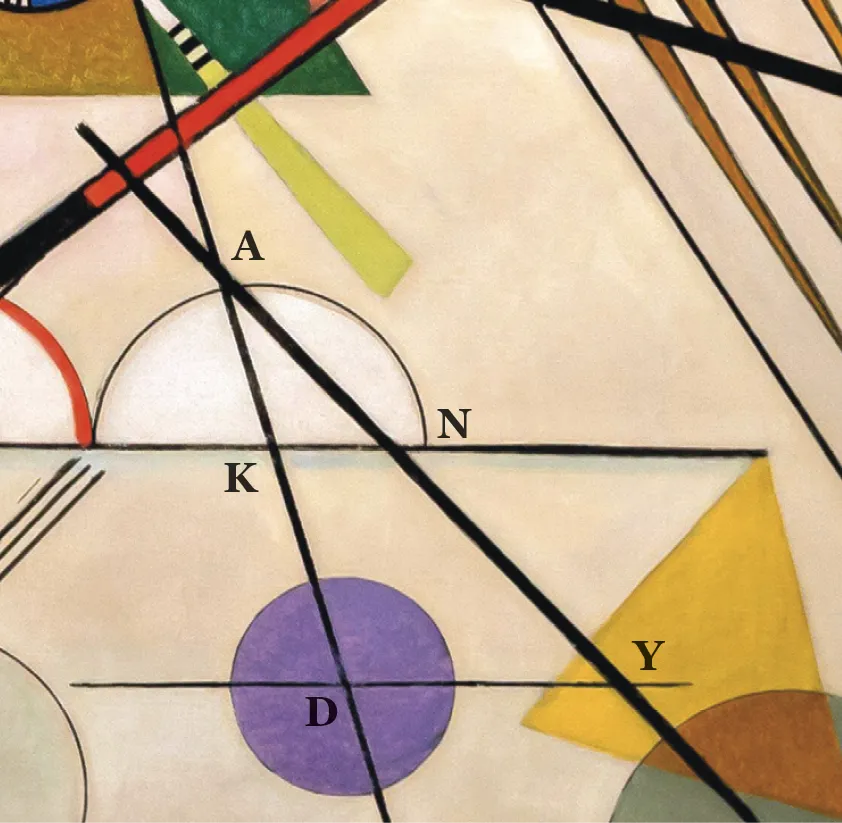
On donne \mathrm{AK}=10,1 \mathrm{~cm}, \mathrm{AD}=23,2 \mathrm{~cm}, \mathrm{AN}=13,4 \mathrm{~cm}, \mathrm{NY}=17,4 \mathrm{~cm}, \mathrm{KN}=6,4 \mathrm{~cm} et \mathrm{DY=14,7 ~cm}.
Les droites \text{(KN)} et \text{(DY)} sont-elles parallèles ?