Chapitre 11
Activités
Découvrir le chapitre : théorème de Thalès
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Thalès de Milet
Thalès de Milet (625-547 av. J.-C.) est un des Sept Sages de l'Antiquité grecque et son nom est entré dans l'Histoire comme celui du premier savant et du premier mathématicien. C'est après un séjour en Égypte, où il étudie les sciences babyloniennes et égyptiennes, qu'il ramène en Grèce des éléments fondateurs de la géométrie. Cinq théorèmes fondamentaux portent son nom, dont celui enseigné dans ce chapitre sur les longueurs de triangles à côtés parallèles. La légende rapporte qu'il aurait calculé la hauteur de la pyramide de Khéops en mesurant son ombre et en la rapportant à celle d'un bâton planté verticalement dans le sol. Aujourd'hui, dans beaucoup d'autres pays que la France, le théorème le plus connu qui porte son nom est celui du triangle rectangle et de son cercle circonscrit. On ne connaît pas d'écrits de Thalès et la première démonstration retrouvée de son théorème sur les triangles à côtés parallèles est celle donnée 250 ans plus tard par Euclide (environ 300 av. J.-C.) dans le livre VI, proposition 2 des Éléments (une encyclopédie mathématique qui constituera l'une des bases du savoir pendant près de deux millénaires).


Faire un schéma qui illustre la méthode utilisée par Thalès pour mesurer la hauteur de la pyramide de Khéops.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Deux triangles emboîtés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
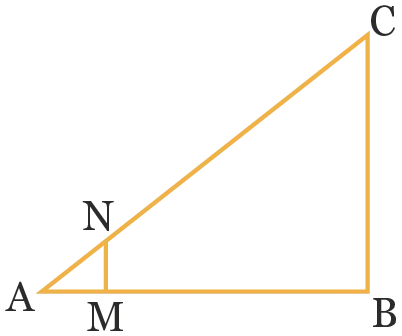
Soit \mathrm{ABC} un triangle. \text M est un point situé sur le côté [\mathrm{AB}] et \mathrm{N} est un point situé sur le côté [\mathrm{AC}]. On a alors deux triangles \mathrm{AMN} et \mathrm{ABC} qui sont emboîtés. De plus, (\mathrm{MN}) est parallèle à (\mathrm{BC}). Voici les longueurs des côtés.
| Triangle \mathrm{ABC} | \mathrm{AB}=10 \mathrm{~cm} | \mathrm{AC}=13 \mathrm{~cm} | \mathrm{BC}=8 \mathrm{~cm} |
|---|---|---|---|
| Triangle \mathrm{AMN} | \mathrm{AM}=2 \mathrm{~cm} | \mathrm{AN}=2,6 \mathrm{~cm} | \mathrm{MN}=1,6 \mathrm{~cm} |
1
S'agit-il d'un tableau de proportionnalité ? Si oui, exprimer son coefficient de proportionnalité à l'aide de trois quotients.Coup de pouce
Chercher un nombre permettant de passer de la première ligne à la deuxième grâce à une multiplication.
2
Que peut-on alors dire du triangle \text{ABC} par rapport au
triangle \text{AMN} ? Justifier.
Bilan
Compléter. Si les triangles \mathrm{AMN} et \mathrm{ABC} sont tels que \mathrm{M}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2Les apparences sont trompeuses
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
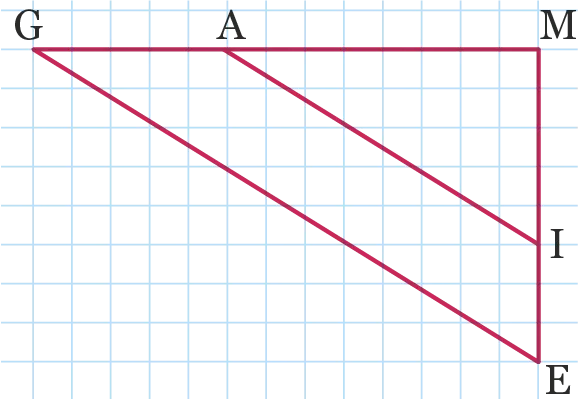
Dans la figure ci-après, chaque carreau mesure 1 cm de côté.
1
Mesurer au rapporteur les angles \widehat{\mathrm{MAI}} et \widehat{\mathrm{AGE}} \text {.}2
Que peut-on alors conjecturer à propos des droites \text {(AI) et (GE)} ?Coup de pouce
Deux angles correspondants de même mesure sont formés par des droites parallèles et une sécante.

3
En détaillant les calculs, déterminer si les quotients
\frac{\mathrm{MA}}{\mathrm{MG}} et \frac{\mathrm{MI}}{\mathrm{ME}} sont égaux.4
Expliquer pourquoi le théorème de Thalès ne peut pas
s'appliquer.5
Reproduire la figure avec GeoGebra puis utiliser la commande
« Angle » pour afficher les valeurs des angles \widehat{\mathrm{MAI}} et \widehat{\mathrm{AGE}} \text {.}6
Conclure à propos de la conjecture faite à la question 2.
Bilan
Dans le cas de deux triangles emboîtés, à quelle condition peut-on être sûr que deux droites ne sont pas parallèles ? Ce raisonnement s'appelle un raisonnement par l'absurde.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 3Quand l'égalité ne suffit pas
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
On donne la figure ci-après, sur laquelle vous allez pouvoir travailler en utilisant notre outil de dessin.2
Justifier que \text {(MN) et (BC)} sont parallèles. 3
Calculer la longueur \text {MN}.4
a. Tracer le cercle de centre \text {M} passant par \text {N}. Ce cercle recoupe le segment \text {[AB]} en \text {P}.
b. Quelle est la longueur du segment \text {[MP]} ?
b. Les droites \text {(MP)} et \text {(BC)} sont-elles parallèles ?
On considère un triangle \text {ABC} avec un point \text {M} sur le côté \text {[AC]} et un point \text {P} sur le côté \text {[AB]}.
Si \frac{\mathrm{M P}}{\mathrm{B C}}=\frac{\mathrm{A M}}{\mathrm{A C}}, peut-on toujours conclure que (\mathrm{M P}) / /(\mathrm{B C}) ?
Si non, déterminer une égalité qui permet de toujours conclure que (\mathrm{M P}) / /(\mathrm{B C}).
5
a. Que peut-on dire des quotients \frac{\mathrm{MP}}{\mathrm{BC}} et \frac{\mathrm{AM}}{\mathrm{AC}} ? b. Les droites \text {(MP)} et \text {(BC)} sont-elles parallèles ?
Bilan
On considère un triangle \text {ABC} avec un point \text {M} sur le côté \text {[AC]} et un point \text {P} sur le côté \text {[AB]}.
Si \frac{\mathrm{M P}}{\mathrm{B C}}=\frac{\mathrm{A M}}{\mathrm{A C}}, peut-on toujours conclure que (\mathrm{M P}) / /(\mathrm{B C}) ?
Si non, déterminer une égalité qui permet de toujours conclure que (\mathrm{M P}) / /(\mathrm{B C}).
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

