Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algorithmique et programmation
Dossier Scratch
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d'équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Prolongement
Chapitre 2
Activités
Addition et soustraction de nombres rationnels
17 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les fractions égyptiennes
Le zoom est accessible dans la version Premium.
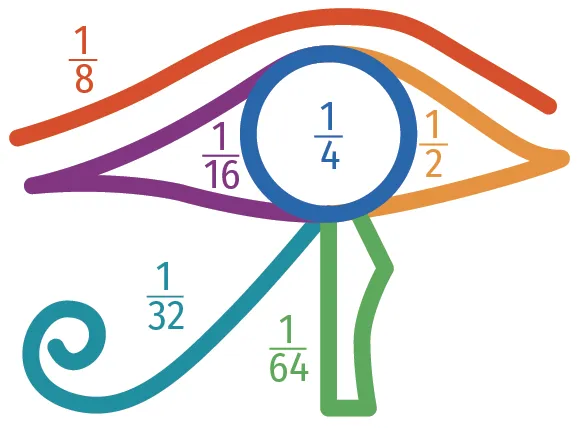
La première grande civilisation à avoir utilisé les fractions est
l'Égypte antique. Les Égyptiens utilisaient des fractions de
numérateur \text{1}, à l'exception de \frac{2}{3}.
Mathématiquement, on peut prouver que tout nombre rationnel peut s'écrire sous la forme d'une somme d'un nombre entier et de fractions de numérateur \text{1}. Pour noter ces fractions, ils utilisaient la décomposition de l'œil du dieu Horus, ou tout simplement leurs nombres surmontés du symbole
.
Mathématiquement, on peut prouver que tout nombre rationnel peut s'écrire sous la forme d'une somme d'un nombre entier et de fractions de numérateur \text{1}. Pour noter ces fractions, ils utilisaient la décomposition de l'œil du dieu Horus, ou tout simplement leurs nombres surmontés du symbole
Le zoom est accessible dans la version Premium.
Par exemple, \text{20} se notait
Le zoom est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
On trouve, par exemple, dans le papyrus de Rhind, les décompositions
\frac{2}{5}=\frac{1}{3}+\frac{1}{15} ou \frac{2}{7}=\frac{1}{4}+\frac{1}{28} ou encore \frac{2}{13}=\frac{1}{8}+\frac{1}{52}+\frac{1}{104} .
Dans d'autres papyrus, on peut trouver différentes décompositions de \frac{2}{45} (qui en possède \text{1967}) telles que :
\frac{2}{45}=\frac{1}{25}+\frac{1}{225} ou \frac{2}{45}=\frac{1}{30}+\frac{1}{90} ou encore \frac{2}{45}=\frac{1}{36}+\frac{1}{60}.
On utilisait la décomposition la plus pratique en fonction du problème à résoudre.
- Dans un rouleau de cuir, on a trouvé la décomposition :
\frac{3}{5}=\frac{1}{2}+\frac{1}{10}.
Inventer une histoire de partage qui pourrait illustrer cette décomposition. Après avoir étudié le chapitre, vérifier que les décompositions ci-dessus sont bien correctes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1À la recherche de points communs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Calculer, puis simplifier, si possible, les expressions suivantes.
a. \text{A}=\frac{5}{3}-\frac{1}{3}
b. \text{B}=\frac{5}{2}+\frac{4}{8}
c. \text{C}=5-\frac{3}{4}
2
Le professeur de mathématiques de Mathis lui demande de calculer la somme \text{D}=\frac{2}{3}+\frac{1}{7}.Quelle distinction peut-on faire entre les dénominateurs de \text{D} et ceux de la question 1 ?
3
a. Dresser les listes des multiples de \text{3} et de \text{7} jusqu'à trouver leur plus petit multiple commun.b. Utiliser ce multiple commun pour réduire les fractions \frac{2}{3} et \frac{1}{7} au même dénominateur, puis calculer \text{D}.
4
Calculer les expressions \mathrm{E}=\frac{3}{5}-\frac{7}{8} et \mathrm{F}=\frac{4}{6}+\frac{7}{4}.Bilan
Comment réduire deux fractions au même dénominateur dans tous les cas ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2Le crible d'Ératosthène
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Dans un tableau de \text{10} lignes et \text{10} colonnes, écrire tous les nombres entiers de \text{1} à \text{100} en commençant par la case en haut à gauche et en complétant ligne par ligne.2
Barrer le nombre \text{1}.3
Entourer le nombre \text{2} dans le tableau puis barrer tous ses
multiples.4
Entourer le nombre \text{3} puis barrer tous ses multiples.5
Entourer le prochain nombre qui n'a pas été barré puis barrer tous ses multiples.6
Procéder ainsi jusqu'au nombre \text{10} puis entourer tous les nombres restant qui n'ont pas été barrés.Cette fonctionnalité est accessible dans la version Premium.
Le zoom est accessible dans la version Premium.
Remarque
Cette technique a été mise au point par Ératosthène, un mathématicien grec de l'Antiquité.
Bilan
Quelle propriété ont en commun les nombres qui ont été entourés ? Pourquoi a-t-on barré le \text{1} au début et ne l'a-t-on pas entouré ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 3Une décomposition bien pratique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Simplifier au maximum les fractions suivantes : \text{A}=\frac{24}{16} ; \text{B}=\frac{27}{21} ; \text{C}=\frac{120}{15} et \text{D}=\frac{72}{81}.2
Le professeur de Johanie lui demande de simplifier la fraction \frac{1575}{2475}. Simplifier cette fraction en utilisant des diviseurs communs à \text{1 575} et \text{2 475}. Que peut-on penser de cette méthode ?3
\text{1 575} peut s'écrire sous la forme 5 \times 315. De même, on pourrait décomposer \text{315} comme un produit de deux facteurs plus petits. Recopier et compléter l'égalité 1575=5 \times 5 \times \ldots,
puis continuer à décomposer tous les facteurs jusqu'à n'avoir que des nombres premiers. L'écriture obtenue s'appelle la décomposition en produit de facteurs premiers.4
En utilisant la même méthode, décomposer en produit de facteurs premiers le nombre \text{2 475}.Bilan
Expliquer comment on peut utiliser ces décompositions pour obtenir la forme la plus simplifiée possible de la fraction \frac{1575}{2475} et rédiger une méthode générale.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah