Mathématiques 2de
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 1
TP / TICE 2
Cinéma
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Un cinéma propose trois tarifs, notés respectivement A, B et C :
A : le billet acheté à l'unité coûte 5,80 € ;
B : une carte de membre coûte 4,35 € par mois, mais permet ensuite de payer chaque entrée 4,35 € ;
C : le tarif qui offre un nombre illimité d'entrées dans le mois est de 34,80 €.
Question préliminaire : Déterminer, pour chaque tarif, le prix total payé dans le mois pour quatre entrées au cinéma.


Question préliminaire : Déterminer, pour chaque tarif, le prix total payé dans le mois pour quatre entrées au cinéma.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Déterminer, en fonction du nombre d'entrées, le tarif le plus intéressant à l'aide d'une des deux méthodes de résolution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
Soit x, le nombre d'entrées achetées au cinéma.
x est un entier naturel compris entre 1 et 10.
1. On note f(x) le prix payé avec le tarif A.
a. Exprimer f(x) en fonction de x.
b. À l'aide de la ligne de saisie, tracer la représentation graphique de f .
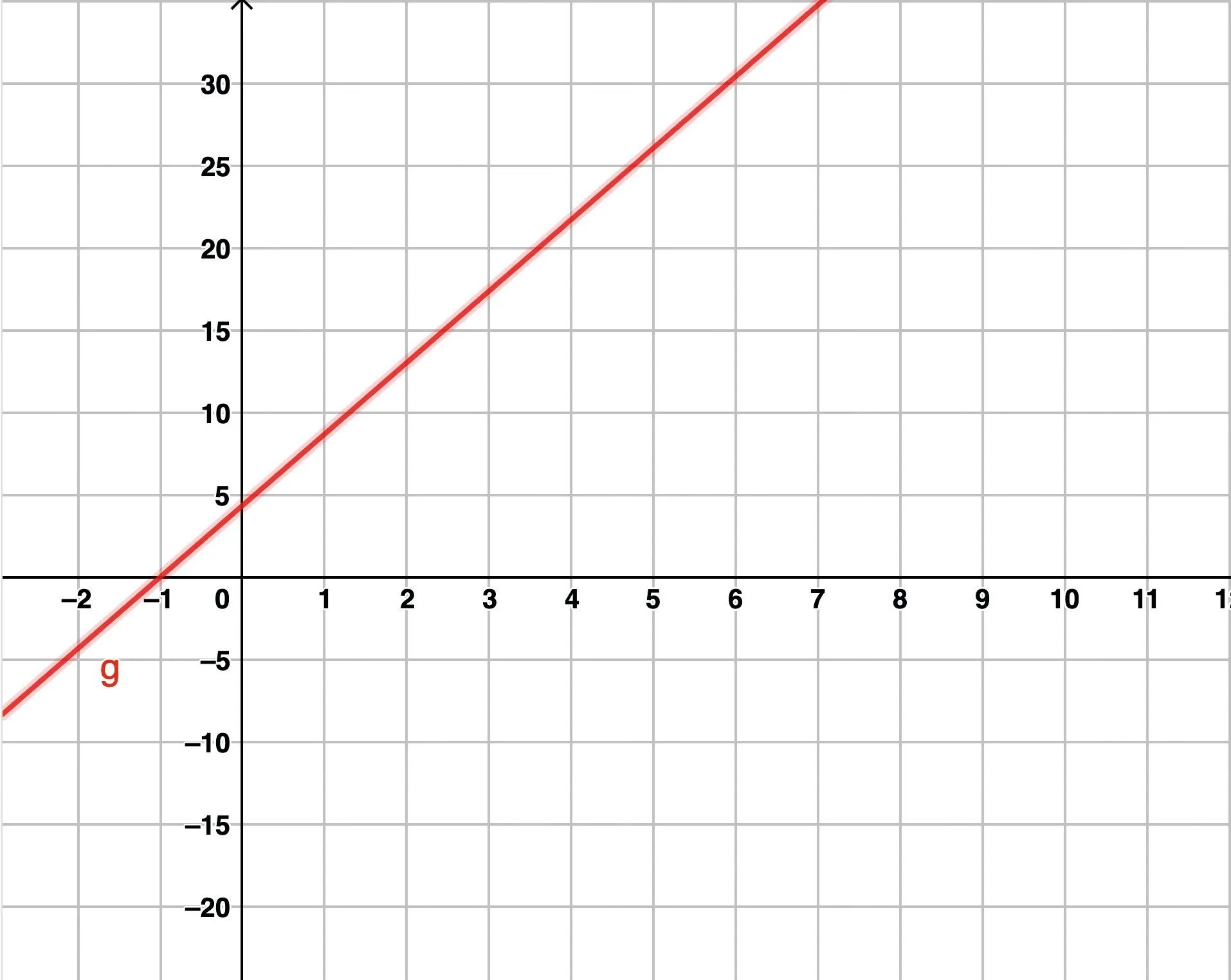
2. On note g(x) le prix payé avec le tarif B.
a. Justifier que g(x) = 4{,}35x + 4{,}35.
b. Tracer sa représentation graphique dans GeoGebra.
Il est possible de changer les graduations sur chaque axe pour visualiser les valeurs qui sont pertinentes.

1. On note f(x) le prix payé avec le tarif A.
a. Exprimer f(x) en fonction de x.
b. À l'aide de la ligne de saisie, tracer la représentation graphique de f .
2. On note g(x) le prix payé avec le tarif B.
a. Justifier que g(x) = 4{,}35x + 4{,}35.
b. Tracer sa représentation graphique dans GeoGebra.
Il est possible de changer les graduations sur chaque axe pour visualiser les valeurs qui sont pertinentes.


3. On note h(x) le prix payé avec le tarif C. Exprimer h(x) en fonction de x puis tracer sa représentation graphique dans GeoGebra.
4. Déterminer graphiquement les nombres d'entrées pour lesquels deux tarifs sont égaux.
5. Conjecturer, selon le nombre d'entrées, le tarif le plus avantageux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
1. Recopier la feuille de calcul suivante.

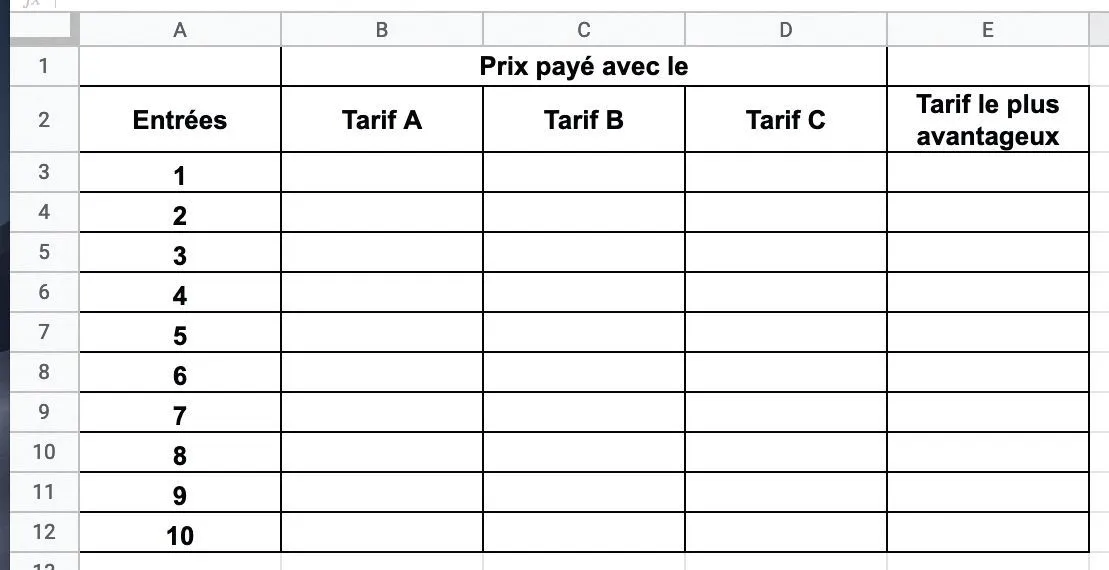
2. On note f(x) le prix payé avec le tarif A.
Exprimer f(x) en fonction de x, puis remplir les cellules de la plage B3:B12.


2. On note f(x) le prix payé avec le tarif A.
Exprimer f(x) en fonction de x, puis remplir les cellules de la plage B3:B12.
3. On note g(x) le prix payé avec le tarif B.
Justifier que g(x) = 4\text{,}35x + 4\text{,}35 puis remplir les cellules
correspondantes.
4. On note h(x) le prix payé avec le tarif C.
Exprimer h(x) en fonction de x, puis remplir les cellules correspondantes.
5. À l'aide de ce tableau de valeurs, déterminer les nombres d'entrées pour lesquels deux tarifs sont égaux.
6. En utilisant la colonne E, conjecturer, selon le nombre d'entrées, le tarif le plus avantageux.
4. On note h(x) le prix payé avec le tarif C.
Exprimer h(x) en fonction de x, puis remplir les cellules correspondantes.
5. À l'aide de ce tableau de valeurs, déterminer les nombres d'entrées pour lesquels deux tarifs sont égaux.
6. En utilisant la colonne E, conjecturer, selon le nombre d'entrées, le tarif le plus avantageux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Déterminer algébriquement le nombre de billets à acheter pour avoir des tarifs égaux deux à deux.
2. Déterminer algébriquement le tarif le plus avantageux en fonction du nombre de billets achetés.
3. Déterminer algébriquement le tarif le plus avantageux en fonction du nombre de billets achetés.
2. Déterminer algébriquement le tarif le plus avantageux en fonction du nombre de billets achetés.
3. Déterminer algébriquement le tarif le plus avantageux en fonction du nombre de billets achetés.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
