Mathématiques 2de
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Partie 2
Histoire des mathématiques
Fonctions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
HistoireTables de valeurs : premiers exemples de la notion de fonction


Extrait d'une traduction arabe de l'Almagest de Ptolémée, IXe siècle.
Le concept de fonction se rencontre dans toutes les disciplines scientifiques et dans les sciences humaines. Il représente initialement l'idée de mettre en relation différentes quantités.
De nombreux exemples d'utilisation nous viennent de l'Antiquité : table de carrés, de racines carrées, d'inverses, de trigonométrie, table de cordes, éphémérides, etc. Ces objets servent à simplifier les calculs ou à aider à trouver sa position. Bien qu'ils soient de véritables tableaux de valeurs de fonctions, on ne peut pas encore réellement parler de conception fonctionnelle.


Table d'inverses, Uruk (Mésopotamie), 300 av. J.-C.


Table d'inverses, Uruk (Mésopotamie), 300 av. J.-C.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
HistoireVers la définition moderne d'une fonction


Leonhard Euler (1707-1783)
Au XIVe siècle, Nicole Oresme exploite l'idée que les lois quantitatives de la nature s'appuient sur des relations fonctionnelles : une fonction peut alors aussi s'exprimer par une description de sa propriété ou par un graphe. Avec l'apport de Viète sur les notations littérales vient le temps des formules. Galilée exploite pleinement tous ces concepts pour l'étude des trajectoires. Descartes expose l'idée d'une relation fonctionnelle entre une grandeur x et une autre grandeur y qui dépend de x . Le premier à utiliser les mots « fonction » et « variable » est Leibniz dans La Méthode inverse des tangentes ou à propos des fonctions (1673). Dans Introductio in analysin infinitorum (1748), Euler définit la fonction d'une quantité variable comme une expression analytique constituée de cette quantité variable et de constantes. On lui doit, entre autres, la notation f(x) et l'étude systématique des fonctions élémentaires.
Après les apports de Cauchy et de Dirichlet et l'avènement de la théorie des ensembles, on peut définir une fonction comme étant une relation entre deux ensembles, pour laquelle chaque élément du premier est en relation avec un unique élément du second.
Après les apports de Cauchy et de Dirichlet et l'avènement de la théorie des ensembles, on peut définir une fonction comme étant une relation entre deux ensembles, pour laquelle chaque élément du premier est en relation avec un unique élément du second.

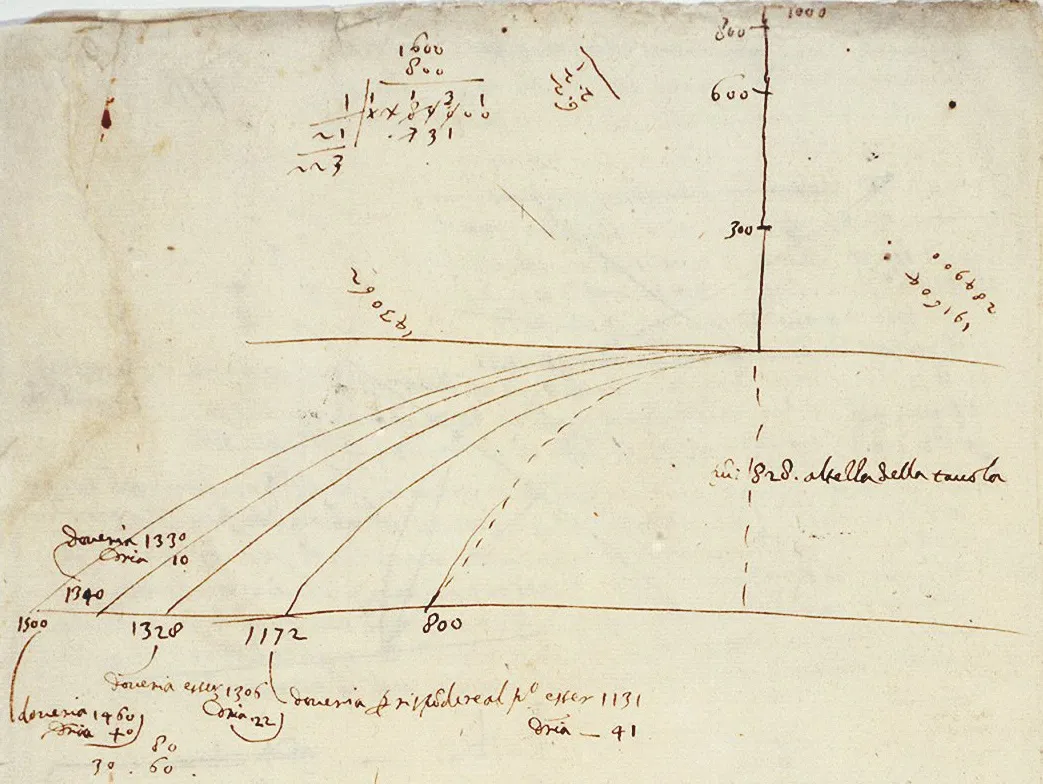
Trajectoires paraboliques d'une bille en chute libre lancée avec différentes vitesses à partir d'une table horizontale. Manuscrit de Galilée - Courtoisie de la Biblioteca Nazionale Centrale, Florence.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question
En quoi les paraboles dessinées par Galilée ou la table d'inverses (qui donne les inverses de différents nombres entiers) peuvent-elles entrer dans le cadre de la définition d'une fonction ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
