Suites arithmétiques

54

[Calculer.]
Pour chacune des suites suivantes, calculer u_{20}. 1. La suite (u_n) est arithmétique de raison r = 3 et telle que u_7 = 12.

2. La suite (u_n) est arithmétique de raison r = 5 et telle que u_{25}= 17.

3. La suite (u_n) est définie par \left\{\begin{array}{l}{u_{0}=3} \\ {u_{n+1}=u_{n}+7}\end{array}\right. pour n \in \N.

4. La suite (u_n) est définie par \left\{\begin{array}{l}{u_{1}=-2} \\ {u_{n+1}=u_{n}-4}\end{array}\right. pour n \in \N.

55

[Calculer.]
Déterminer si les suites suivantes sont arithmétiques. Si oui, donner le premier terme et la raison. 1. Pour tout n \in \N, u_{n}=\dfrac{n+5}{n+1}.

2. Pour tout n \in \N, u_{n}=\dfrac{-3 n+5}{8}.

3. Pour tout n \in \N, u_{n}=\dfrac{n^{2}+4 n+3}{n+3}.

4. Pour tout n \in \N, u_{n}=\dfrac{n^{2}+1}{n+2}.

58

[Représenter.]
Dans le repère orthonormé ci-dessous, on a représenté quelques termes de trois suites arithmétiques.
Pour chacune d'elle, déterminer le premier terme, la raison ainsi que l'expression de u_n en fonction de n. Donner la valeur de u_3 et u_6.

1. Suite verte

2. Suite rouge

3. Suite violette

59

[Modéliser.]
Lorentz place une somme de 1 000 euros au taux simple annuel de 5 % ; c'est-à-dire que chaque année, la somme placée augmentera de 5 % de la somme initiale. Pour tout entier naturel n, u_n désigne le capital de Lorentz n années après son placement. 1. Déterminer u_0, u_1, u_2 et u_3.

2. Exprimer u_{n+1} en fonction de u_n.

3. Prouver que la suite (u_n) est arithmétique. Donner sa raison et son premier terme u_0 .

4. En déduire une expression de u_n en fonction de n.

5. Au bout de combien d'années le capital de Lorentz aura-t-il doublé ?

60

[Calculer.]
Calculer les sommes suivantes. 1. \mathrm{S}=1+2+3+\ldots+73.

2. \mathrm{T}=1+4+7+\ldots+40.

3. \mathrm{U}=71+72+73+\ldots+100.

4. \mathrm{V}=2+4+6+\ldots+50.

61

[Calculer.]
Le but de l'exercice est de manipuler le symbole \Sigma. 1. Écrire chaque somme en développant puis la calculer.
a. \mathrm{S}= \mathop{\sum}\limits_{i=0}\limits^{15} (2i+1)

b. \mathrm{T}= \mathop{\sum}\limits_{i=2}\limits^{7}(3 i-2)

2. Écrire chaque somme avec le symbole \Sigma puis la calculer.
a. \mathrm{U}=3+6+9+\ldots+81

b. \mathrm{V}=5+9+13+\ldots+45

63

[Calculer.]
On souhaite empiler des allumettes. Pour n \in \N^*, on note a_n le nombre d'allumettes nécessaire pour construire la ligne du niveau n . Ainsi, a_1=2 et a_2=4.
1. Déterminer les quatre premiers termes de la suite.

2. Exprimer a_n en fonction de n avec n \in \N^* puis en déduire la nature de la suite.

3. Combien d'allumettes totales seront nécessaires pour construire la dixième étape ?

64

[Modéliser.]
Une famille décide d'épargner afin de pouvoir s'offrir un voyage en Égypte.
La première année, elle économise 500 euros. Chaque année, elle augmente la somme épargnée de 100 euros.


Pour n \geqslant 1 , on note s_n , la somme épargnée l'année n . 1. Déterminer s_1, s_2 et s_3. Pour tout n de \N^*, exprimer s_{n+1} en fonction de s_n .

2. En déduire l'expression de s_n en fonction de l'entier naturel n \geqslant 1.

3. À l'aide de la calculatrice, déterminer dans combien d'années la famille pourra partir en voyage sachant que le voyage coûte 4 200 euros.

66

Tableur

[Représenter.]
Voici un extrait de tableur qui représente une suite (u_n) définie pour tout entier naturel n .

1. Déterminer l'expression de u_n en fonction n.

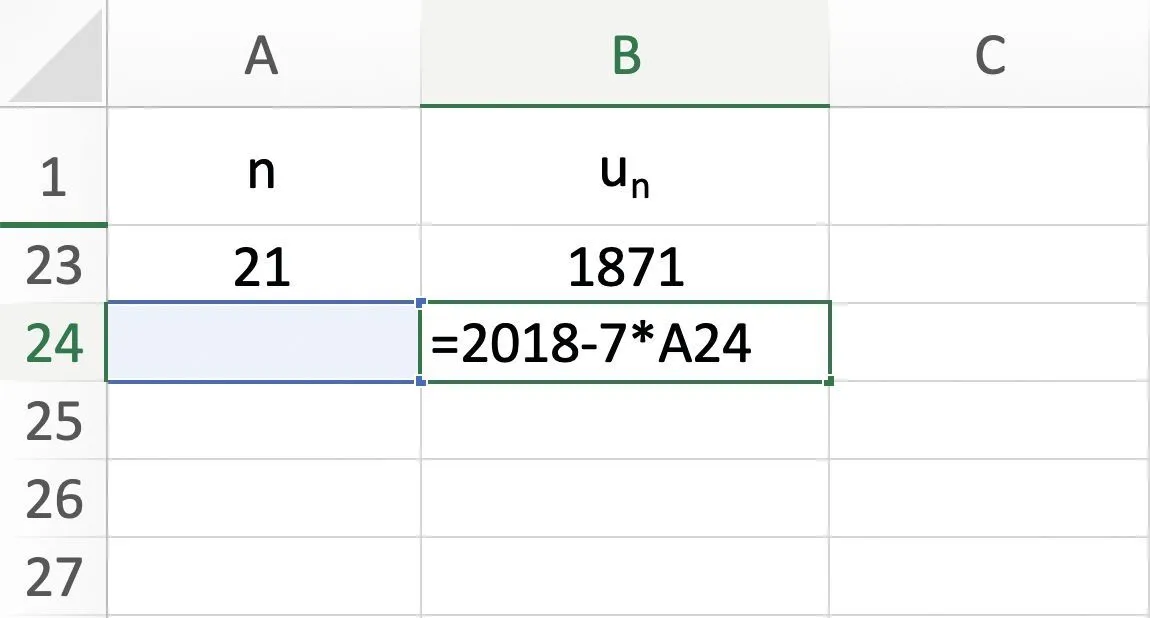
2. Quelle est la nature de la suite (u_n) ? Justifier.

3. Quel est son sens de variation ? Justifier.

4. Calculer le premier terme u_0.

67

[Calculer.]
En 2017, le nombre d'abonnés à une page de réseau social d'un artiste était de 9 000. On suppose que, chaque année, il obtient 1 500 fans supplémentaires.
f_n désigne le nombre d'abonnés en 2017 +\ n pour tout entier naturel n. 1. Calculer le nombre d'abonnés en 2018 et 2019.

2. Exprimer f_{n+1} en fonction de f_n.

3. Quelle est la nature de la suite ? En déduire une expression de f_n en fonction de n.

4. Existe-t-il une année pour laquelle le nombre d'abonnés aura triplé par rapport à 2017 ? Si oui, laquelle ?