Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 1
Entrainement 3
Suites géométriques
10 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
[Calculer.] Pour chacune des suites, calculer v_{20}. 1. La suite (v_n) est géométrique de raison q = 3 et telle que v_3 =12.
2. La suite (v_n) est géométrique de raison q = -2 et telle que v_{31} =32.
3. La suite (v_n) est définie par \left\{\begin{array}{l}{v_{0}=-5} \\ {v_{n+1}=2 v_{n}, n \in \mathbb{N}}\end{array}\right.
4. La suite (v_n) est définie par \left\{\begin{array}{l}{v_{1}=2\,048} \\ {v_{n+1}=-\dfrac{1}{2} v_{n}, n \in \mathbb{N}}\end{array}\right.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
[Calculer.] Déterminer si les suites suivantes sont géométriques. Si oui, donner le premier terme et la raison. 1. Pour tout n \in \N, v_{n}=\dfrac{4^{n}}{3^{n+1}}.
2. Pour tout n \in \N, v_{n}=(-7)^{n}.
3. Pour tout n \in \N, v_{n}=5 n+2^{n}.
4. Pour tout n \in \N, v_{n}=\dfrac{1}{3^{n}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
[Calculer.] Dans chaque cas, on considère deux termes d'une suite géométrique (v_n) définie sur \N. Déterminer la raison et le premier terme puis exprimer v_n en fonction de n, pour tout n \in \N. 1. v_3=6 et v_8=1\,458.
2. v_6=-18 et v_{12}=-\dfrac{9}{32}.
3. v_{10}=15 et v_{15}=46\, 875.
4. v_{21}=65\, 536 et v_{23}=262\, 144.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
[Calculer.] Calculer les sommes suivantes. 1. \mathrm{S}=1+4+16+\ldots+262\,144
2. \mathrm{T}=3-6+12-24+\ldots+192
3. \mathrm{U}=9+3+1+\dfrac{1}{3}+\ldots+\dfrac{1}{729}
4. \mathrm{V}=1+0{,}5+0{,}25+\ldots+0{,}031 25
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
[Calculer.]
Le but de l'exercice est de manipuler le symbole \Sigma. 1. Écrire chaque somme en développant puis la calculer.
a. \mathrm{S}=\mathop{\sum}\limits_{i=0}\limits^{15} 2^i
b. \mathrm{T}=\mathop{\sum}\limits_{i=2}\limits^{7} \left( \dfrac{1}{4} \right)^i
2. Écrire chaque somme avec le symbole \Sigma puis la calculer.
a. \mathrm{U}=1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+\ldots+\dfrac{1}{256}
b. \mathrm{V}=2+6+18+54+\ldots+13 \, 122
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
En médecine
[Modéliser.] Afin de greffer 10 cm² de peau à une personne brûlée, on lui en prélève 20 mm². La culture permet d'augmenter de 15 % la surface de peau chaque jour.
Dans combien de jours pourra se faire la greffe de peau ? 1. Calculer la surface les deuxième et troisième jours.
2. Pour tout entier naturel n , v_n modélise la surface de peau le jour n . Écrire une relation entre v_{n+1} et v_n.
3. Quelle est la nature de la suite (v_n) ?
4. Donner l'expression de v_n en fonction de n .
5. Répondre au problème posé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
En SNT
[Modéliser.] Pour stocker des photos numériques, on utilise un algorithme de compression. On estime qu'à chaque niveau de compression, la taille diminue de 21,4 %.
La taille initiale d'une photo est de 4 Mo. On pose T_0 =4 et, pour tout entier naturel non nul n , T_n désigne la taille de cette photo après une compression de niveau n. 1. Calculer T_1 et T_2 .
2. Pour tout n \in \N, exprimer T_{n+1} en fonction de T_n . En déduire la nature de la suite (T_n).
3. Exprimer T_n en fonction de n .
4. Peut-on stocker 20 000 photos sur une clé USB d'une capacité de 32 Go ? Avec quelle compression ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
Algo
[Calculer.]
On reprend l'énoncé de l'exercice précédent. 1. Écrire un algorithme afin de déterminer le niveau de compression nécessaire pour stocker 100 000 photos sur une clé USB d'une capacité de 64 Go.
2. Le programmer sous Python afin de répondre à la question.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
[Chercher.]
Déterminer le sens de variation des suites géométriques suivantes définies sur \N.
1. a. v_{n}=\dfrac{4^{n}}{3^{n+1}}
b. v_{n}=(-7)^{n}
c. v_{n}=5^{n} \times 2^{n}
d. v_{n}=\dfrac{1}{3^{n}}
b. v_{n}=(-7)^{n}
c. v_{n}=5^{n} \times 2^{n}
d. v_{n}=\dfrac{1}{3^{n}}
2. a. v_{3}=6 et v_{8}=1\,458
b. v_{6}=-18 et v_{12}=-\dfrac{9}{32}
c. v_{10}=15 et v_{15}=46\, 875
d. v_{21}=65\, 536 et v_{23}=262\, 144
b. v_{6}=-18 et v_{12}=-\dfrac{9}{32}
c. v_{10}=15 et v_{15}=46\, 875
d. v_{21}=65\, 536 et v_{23}=262\, 144
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78
[Calculer.]
Soit (u_n) la suite définie par \left\{\begin{array}{l}{u_{0}=-3} \\ {u_{n+1}=\dfrac{1}{2} u_{n}-4, n \in \mathbb{N}}\end{array}\right.
On pose v_n = u_n +8 pour tout n \in \N. 1. Montrer que la suite (v_n) est géométrique. Donner sa raison et son premier terme.
2. Exprimer v_n puis u_n en fonction de n .
3. Déterminer le sens de variation de chaque suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79
Tableur
[Modéliser.]
On considère la suite géométrique (u_n) définie par u_{n}=\left(1-\dfrac{1{,}23}{100}\right)^{n} pour tout n \in \N. 1. Déterminer le premier terme et la raison de cette suite.
2. Cette suite est-elle croissante ou décroissante ?
3. On cherche à déterminer le plus petit nombre n tel que u_n \lt 0{,}5 .
Le zoom est accessible dans la version Premium.
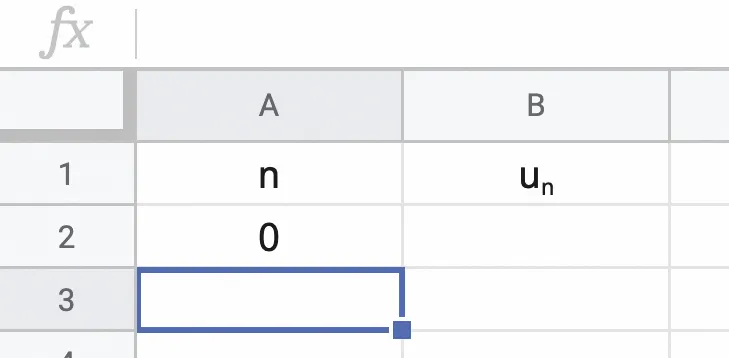
a. Reproduire la feuille de calcul ci-dessus et entrer dans la cellule A3 la formule permettant d'afficher toutes les valeurs de n lorsqu'on l'étire vers le bas. Étirer cette cellule jusqu'à la ligne 101.
GeoGebra
b. Entrer dans la cellule B2 la formule permettant d'afficher la valeur de u_0 à partir de la valeur de la cellule A2 puis étirer cette cellule jusqu'à la ligne 101.
c. Conclure.
Les archéologues et les paléontologues sont parfois amené(e)s à déterminer l'âge d'un squelette ou d'un fossile. Ils utilisent pour cela la datation au carbone 14 qui est étudiée dans le cours d'enseignement scientique. Cette technique de datation nécessite l'utilisation de suites numériques similaires à celle étudiée dans l'exercice précédent ainsi que la fonction exponentielle étudiée dans le chapitre 6.
c. Conclure.
Dans la vie professionnelle
Le zoom est accessible dans la version Premium.
Les archéologues et les paléontologues sont parfois amené(e)s à déterminer l'âge d'un squelette ou d'un fossile. Ils utilisent pour cela la datation au carbone 14 qui est étudiée dans le cours d'enseignement scientique. Cette technique de datation nécessite l'utilisation de suites numériques similaires à celle étudiée dans l'exercice précédent ainsi que la fonction exponentielle étudiée dans le chapitre 6.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
80
[Modéliser.]
Deux amis partent pour une randonnée de 200 km. Le premier jour, ils marchent 20 km. En raison de la fatigue, la distance parcourue diminue de 5 % par jour. Déterminer à l'aide de la calculatrice en combien de jours ils termineront leur randonnée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
81
[Modéliser.]
Clément se sert plusieurs fois de la pizza. À chaque fois, il mange la moitié de ce qui reste. 1. Quelle portion de pizza a-t-il mangée après s'être servi cinq fois ?
2. Quelle part de pizza restera-t-il pour son frère Florian ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82
[Modéliser.]
Le format d'une feuille de papier est tel que le rapport entre la longueur et la largeur soit constant.
La surface du format A0 est de 1 m². Pour le format A1, la longueur est divisée par deux et devient la nouvelle largeur. On recommence ainsi pour chaque format en divisant la longueur du format précédent par deux et en conservant le même rapport entre la longueur et la largeur.
Le zoom est accessible dans la version Premium.
1. On souhaite que le rapport des longueurs aux largeurs soit toujours le même.
a. À partir de l'égalité \dfrac{\mathrm{L}_{1}}{\ell_{1}}=\dfrac{\mathrm{L}_{0}}{l_{0}} en déduire la valeur du rapport \dfrac{\mathrm{L}_{0}}{\ell_{0}}.
b. Sachant que la feuille au format A0 a une aire de 1 m², en déduire les valeurs \mathrm{L}_0 et \ell_{0}.
Le zoom est accessible dans la version Premium.
a. À partir de l'égalité \dfrac{\mathrm{L}_{1}}{\ell_{1}}=\dfrac{\mathrm{L}_{0}}{l_{0}} en déduire la valeur du rapport \dfrac{\mathrm{L}_{0}}{\ell_{0}}.
b. Sachant que la feuille au format A0 a une aire de 1 m², en déduire les valeurs \mathrm{L}_0 et \ell_{0}.
2. a. Prouver que la suite (L_n) des longueurs des feuilles A_n est une suite géométrique de raison q=\dfrac{\sqrt{2}}{2}.
b. Quel est son sens de variation ?
c. Donner une expression du terme général L_n en fonction de n \in \N .
3. Quelle est la nature de la suite (\ell_n) des largeurs ? Quel est son sens de variation ?
4. Retrouver alors les dimensions d'une feuille A4.
b. Quel est son sens de variation ?
c. Donner une expression du terme général L_n en fonction de n \in \N .
3. Quelle est la nature de la suite (\ell_n) des largeurs ? Quel est son sens de variation ?
4. Retrouver alors les dimensions d'une feuille A4.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah