Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Partie 4
Histoire des mathématiques
Probabilités et statistiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
HistoireNaissance des probabilités indépendantes et conditionnelles
Les probabilités conditionnelles sont omniprésentes dans la vie courante et leur utilisation inappropriée mène facilement à de fausses interprétations. Un événement a-t-il plus de chances de se réaliser si sa probabilité vaut 0,0001 ou s'il se réalise 1 fois sur 10 000 ? La perception de probabilité varie pour chaque individu, d'où l'importance de bien en maîtriser les notions de base. Après le traité de Huygens, De ratiociniis in ludo aleae (1657), cette branche des mathématiques connaîtra un rapide développement.




Dans The Doctrine of Chances (voir l'extrait) publié à Londres en 1718, Abraham de Moivre (1667-1754) est le premier mathématicien à aborder la notion d'indépendance d'événements. En 1733, il utilise la formule de Stirling pour décrire la loi normale comme une approximation de la loi binomiale qu'il venait de formuler. C'est à une œuvre de Thomas Bayes (1702-1761), publiée à titre posthume, que l'on doit la première théorie sur les probabilités conditionnelles.




Dans The Doctrine of Chances (voir l'extrait) publié à Londres en 1718, Abraham de Moivre (1667-1754) est le premier mathématicien à aborder la notion d'indépendance d'événements. En 1733, il utilise la formule de Stirling pour décrire la loi normale comme une approximation de la loi binomiale qu'il venait de formuler. C'est à une œuvre de Thomas Bayes (1702-1761), publiée à titre posthume, que l'on doit la première théorie sur les probabilités conditionnelles.


Extrait du livre de Moivre, The Doctrine of Chances, 1718.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
HistoireVariable aléatoire et espérance
L'histoire des probabilités contribue à la réflexion sur la codification d'une théorie scientifique. De grosses avancées ont été faites à partir du XVIIe siècle mais il faudra attendre le début des années 1930 pour que la description actuelle en termes d'univers s'impose. La notion de variable aléatoire apparaît alors comme une fonction particulière définie sur son univers.

La famille Bernoulli est une famille de scientifiques suisses : Jacques (1654-1705), Jean (1667-1748) et Daniel (1700-1782) en sont les trois mathématiciens les plus célèbres.
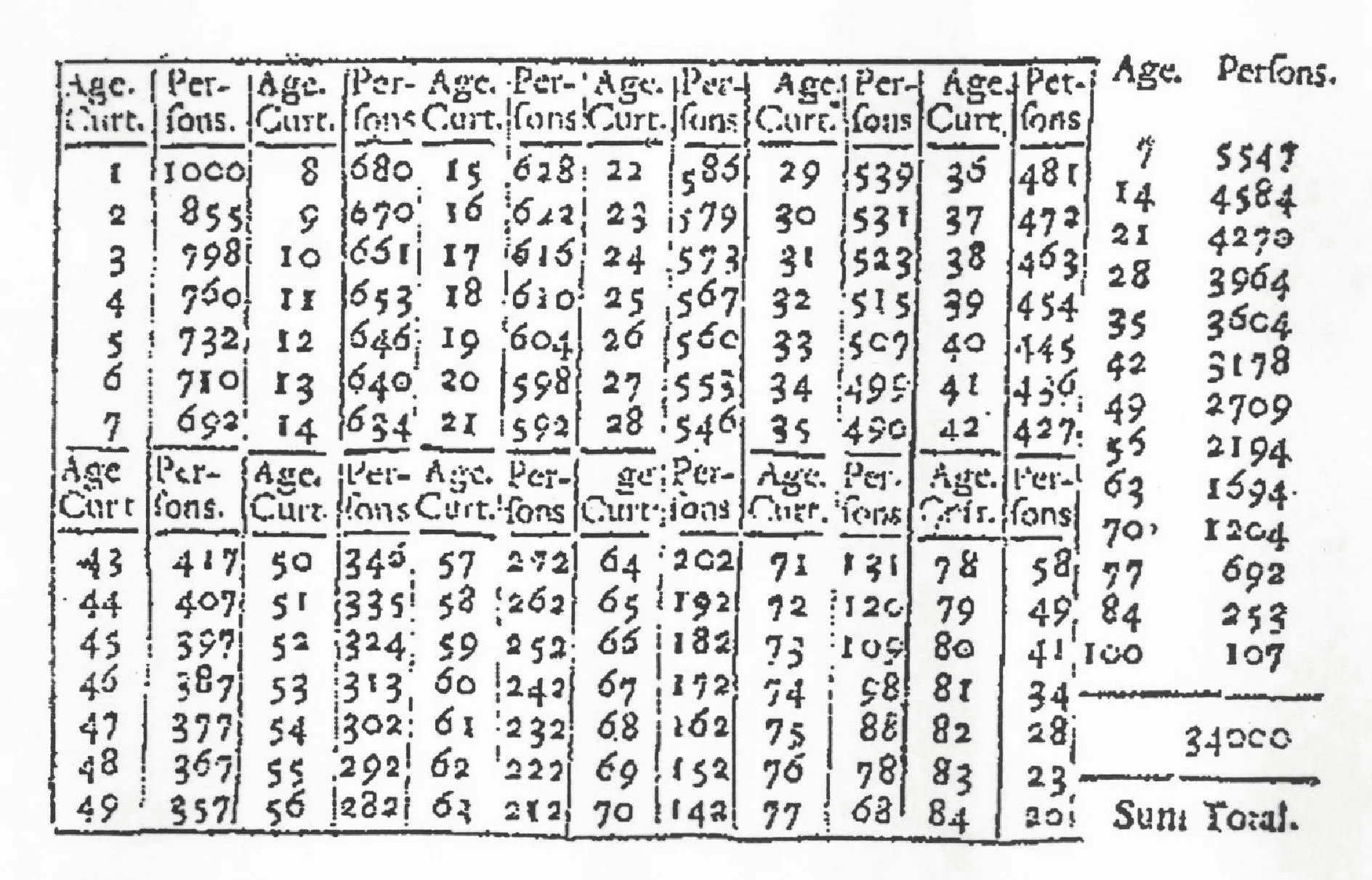
Daniel a écrit en 1760 son Essai d'une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l'inoculation pour la prévenir. C'est le premier texte mathématique appliqué à la médecine. Pour établir cette conclusion, il utilise ses connaissances sur les probabilités (variables aléatoires et espérance), ainsi que la table de mortalité établie par Edmond Halley (1656-1742). Suite aux travaux sur la vaccination du médecin Edward Jenner (1749-1823), la vaccination contre la variole devient systématique et, en 1980, l'OMS (Organisation mondiale de la santé) déclare la maladie officiellement éradiquée.
Daniel a écrit en 1760 son Essai d'une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l'inoculation pour la prévenir. C'est le premier texte mathématique appliqué à la médecine. Pour établir cette conclusion, il utilise ses connaissances sur les probabilités (variables aléatoires et espérance), ainsi que la table de mortalité établie par Edmond Halley (1656-1742). Suite aux travaux sur la vaccination du médecin Edward Jenner (1749-1823), la vaccination contre la variole devient systématique et, en 1980, l'OMS (Organisation mondiale de la santé) déclare la maladie officiellement éradiquée.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
1. Comment expliquer qu'Abraham de Moivre, né en France en 1667, ait principalement publié ses recherches en anglais ? (Indice : révocation de l'édit de Nantes, 1685.)
2. Déterminer la moyenne d'âge de la population étudiée par Edmond Halley pour établir sa table de mortalité (il faut y ajouter 1 300 nouveaux-nés).
3. Après avoir étudié le chapitre 11, donner la formule de Bayes.
2. Déterminer la moyenne d'âge de la population étudiée par Edmond Halley pour établir sa table de mortalité (il faut y ajouter 1 300 nouveaux-nés).
3. Après avoir étudié le chapitre 11, donner la formule de Bayes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
