On cherche à calculer \text{P(B)} avec différentes valeurs de \text{P(R),} \mathrm{P(\overline{R}) ,} \mathrm{P_{R}(B)} et \mathrm{P_{\overline{R}}(B)} choisies au hasard. On détermine ensuite si on a simultanément :

\mathrm{P(B)} supérieure à la valeur de référence (ligne 2) ;

\mathrm{P_{R}(B)} inférieure à la valeur de référence (ligne 2) ;

\mathrm{P_{\overline{R}}(B)} inférieure à la valeur de référence (ligne 2).

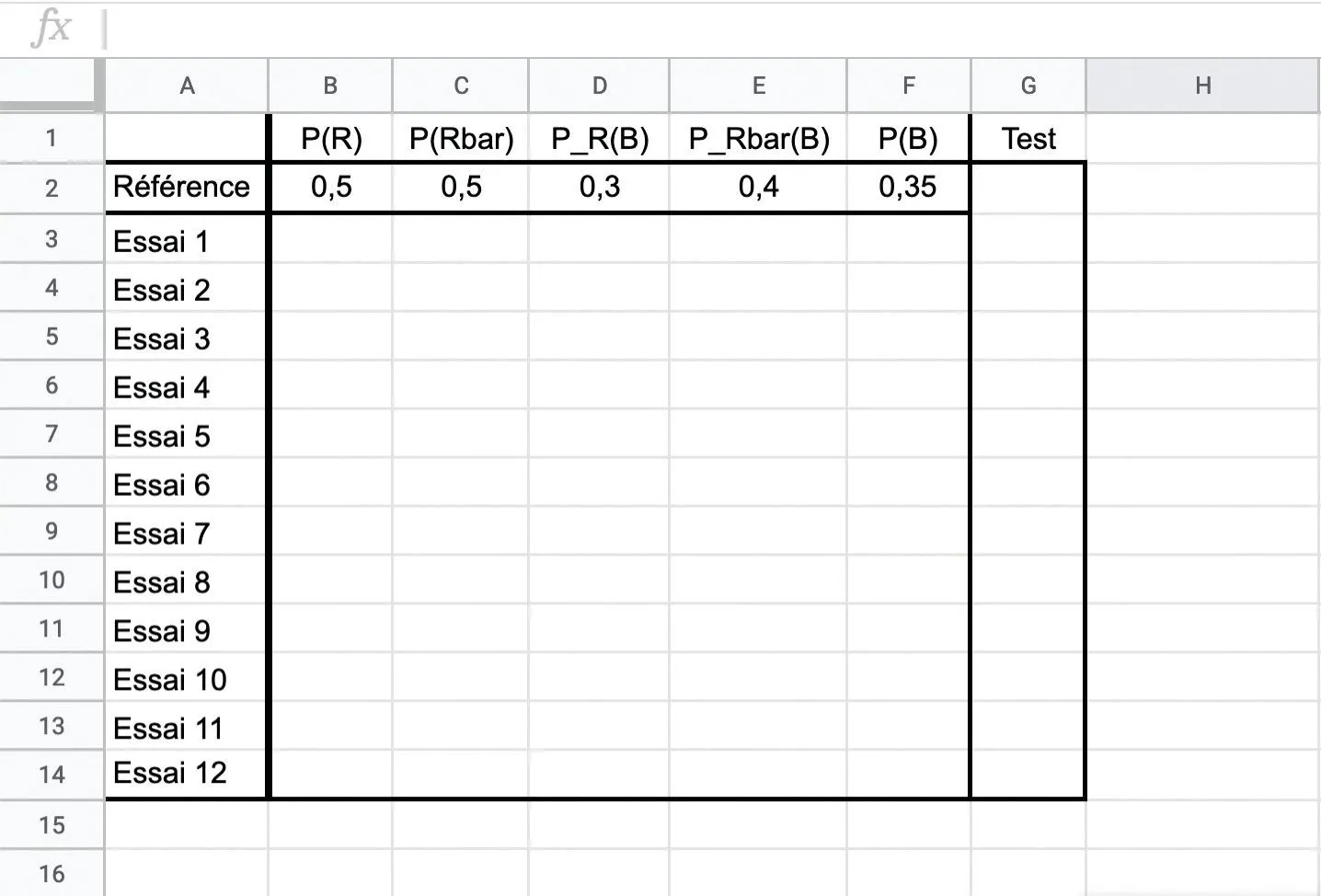
1. Recopier la feuille de calcul ci-dessus.
a. Que faut-il écrire dans les cellules B3, C3, D3 et E3 pour obtenir des probabilités ?

b. Comment calculer \mathrm{P(B)} dans F3 ?

2. Quelle formule écrire dans la cellule G3 pour tester les trois conditions de la consigne ?

3. En copiant la ligne 3 vers le bas au moins 20 fois, faire apparaître une situation réalisant les trois conditions de la consigne.

\text{A} est le point fixe de coordonnées (0\,; 0).

Le point \text{B} est le point fixe de coordonnées (0\,;1).

Le point \text{E} est un point mobile appartenant au segment [\text{AB}].

Le point \text{C} peut varier sur l'axe des abscisses entre \text{A} et le point de coordonnées (2\,;0).

\text{ACDB} est un rectangle.

Le point \text{G} peut varier entre \text{A} et \text{C} avec \mathrm{AG} \leqslant 1 et \mathrm{GC} \leqslant 1.

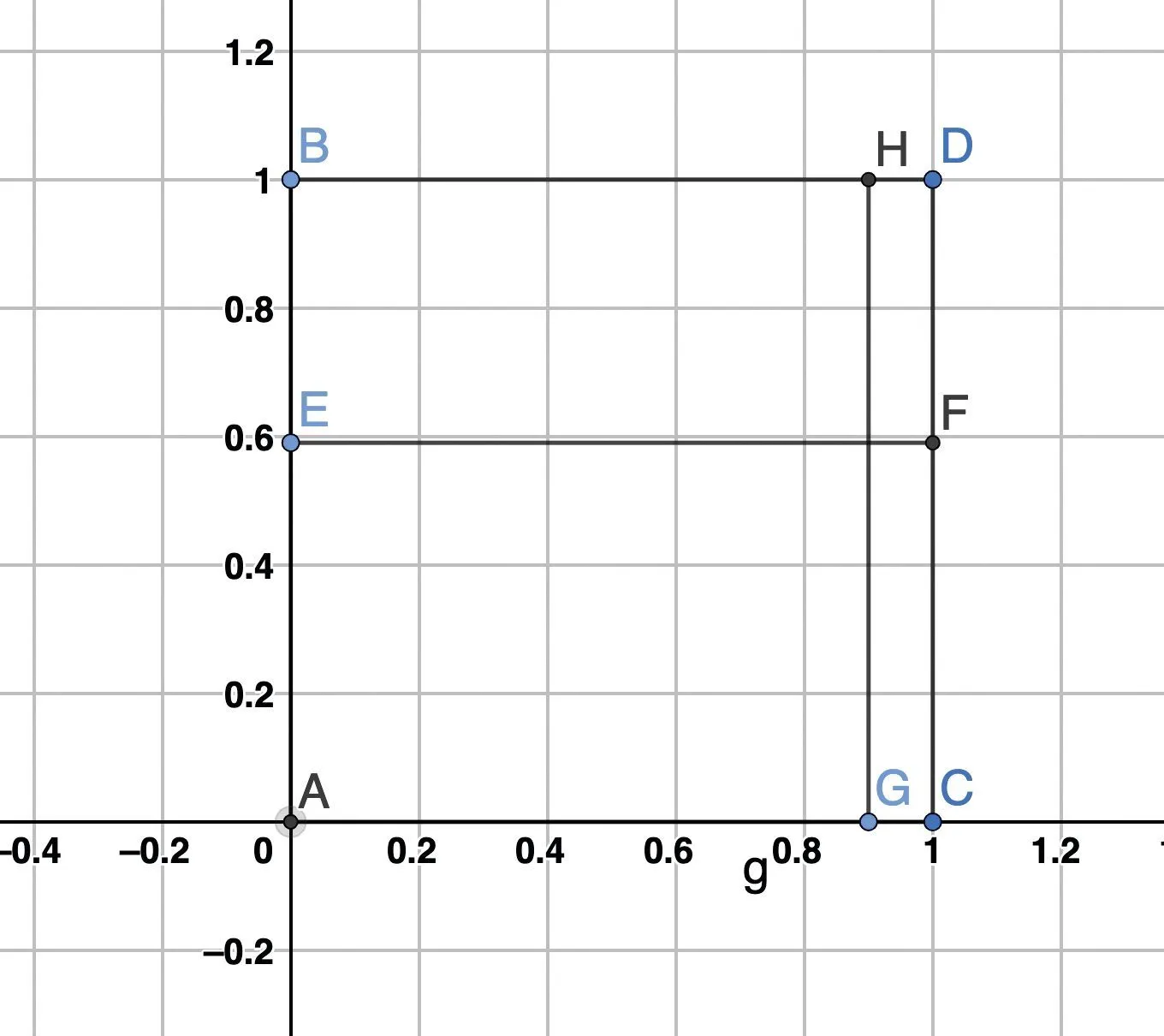
2. Si l'on note \mathrm{P(R) = BE }, interpréter \text{AE} en termes de probabilité.

3. Si l'on pose \mathrm{AG = P_{R}(B)} et \mathrm{GC = P_{\overline{R}}(B),} colorier sur la figure une figure dont l'aire est \text{P(B).}

4. En faisant varier la position des points \text{E} , \text{C} et \text{G} , établir qu'une baisse de \mathrm{P_{R}(B)} et de \mathrm{P_{\overline{R}}(B)} n'implique pas une baisse de \mathrm{P(B)}.

Voici un exemple historique illustrant le paradoxe de Simpson : en 1964, les États-Unis ont voté une loi historique, le Civil Rights Act, qui fut un pas déterminant vers l'abolition de la ségrégation raciale. En comparant les résultats des États du Nord et ceux du Sud du pays, on constate que les démocrates ont davantage voté que les républicains en faveur de la loi, aussi bien au Nord qu'au Sud. Pourtant, sur l'ensemble du pays, 80 % des républicains ont voté en sa faveur, contre seulement 61 % des démocrates. Étonnant !

1. Comment peut-on expliquer ce paradoxe ?

2. Retrouver sur internet d'autres exemples illustrant ce paradoxe.

3. Visionner une vidéo pour en apprendre plus sur le paradoxe de Simpson :