Fiche méthode 21
Exclusivité numérique
Utiliser le langage de programmation Python
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Présentation
Python est un langage de programmation développé depuis 1989. Sa syntaxe simple, basée sur l'indentation plutôt que sur les symboles, en fait l'un des langages les plus utilisés.
Pour pouvoir programmer en Python, on peut opter pour une utilisation en ligne avec le ou bien pour différentes distributions comme ou . Les parties suivantes s'intéressent à deux aspects de la programmation en Python pour la Physique-Chimie, à savoir l'import de données et la représentation graphique.
Pour pouvoir programmer en Python, on peut opter pour une utilisation en ligne avec le ou bien pour différentes distributions comme ou . Les parties suivantes s'intéressent à deux aspects de la programmation en Python pour la Physique-Chimie, à savoir l'import de données et la représentation graphique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Import de données
Pour importer des données dans un programme Python, on peut avoir recours à la bibliothèque numpy qui permet notamment de récupérer des données dans un fichier .txt et de les mettre en forme dans un tableau.
On présente ci-dessous des données obtenues à partir d'un logiciel de pointage vidéo. Suivant les logiciels, la forme du fichier de données peut différer. Plusieurs points importants sont à identifier :
❯ Fichier de données nommé donnees.txt.
L'ensemble de ces paramètres sont à identifier pour pouvoir utiliser correctement la fonction numpy.loadtxt(). On peut illustrer le but de chaque paramètre dans l'exemple ci-dessous :
❯ Programme Python permettant de récupérer des données dans un fichier externe donnees.txt, situé dans le même dossier, à l'aide de la fonction programmation.
On présente ci-dessous des données obtenues à partir d'un logiciel de pointage vidéo. Suivant les logiciels, la forme du fichier de données peut différer. Plusieurs points importants sont à identifier :
- le type de séparation entre les colonnes (un espace, une tabulation, une virgule, etc.) ;
- l'utilisation de la virgule ou du point pour séparer la partie entière de la partie décimale des valeurs. S'il s'agit d'une virgule, on peut réaliser une commande « Rechercher/Remplacer » automatique pour convertir toutes les virgules en points ;
- le nombre de lignes à ignorer pour l'import des données (titres des colonnes, unités éventuelles, etc.) ;
- les colonnes à importer.
| t | x | y |
| s | >m | m |
| 0 | 0,273 6 | 1,501 2 |
| 0,033 4 | 0,271 2 | 1,484 3 |
| 0,066 7 | 0,271 2 | 1,464 9 |
| 0,1001 | 0,266 3 | 1,435 8 |
| 0,133 5 | 0,2688 | 1,389 8 |
| 0,166 8 | 0,2688 | 1,336 6 |
| 0,2002 | 0,268 8 | 1,273 6 |
| 0,233 6 | 0,268 8 | 1,203 4 |
| 0,266 9 | 0,268 8 | 1,1186 |
| 0,3003 | 0,273 6 | 1,026 6 |
| 0,333 7 | 0,266 3 | 0,929 8 |
| 0,3670 | 0,268 8 | 0,8111 |
| 0,4004 | 0,266 3 | 0,6828 |
| 0,4338 | 0,266 3 | 0,564 2 |
❯ Fichier de données nommé donnees.txt.
L'ensemble de ces paramètres sont à identifier pour pouvoir utiliser correctement la fonction numpy.loadtxt(). On peut illustrer le but de chaque paramètre dans l'exemple ci-dessous :
- fname : le nom du fichier, sous forme de chaîne de caractères (ici « donnees.txt ») ;
- unpack : si True, chaque colonne est séparée des autres ;
- usecols : permet la sélection des colonnes à importer (ici, la première, la seconde et la troisième) ;
- delimiter : précise le symbole de séparation des colonnes (ici, \t correspond au symbole d'une tabulation) ;
- skiprows : indique le nombre de lignes à sauter avant l'import des données (ici, les deux premières sont ignorées).
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
# Lecture des données du fichier txt
t, x, y = np.loadtxt('donnees.txt', unpack = True, usecols = (0, 1, 2), delimiter = '\t', skiprows = 2)
❯ Programme Python permettant de récupérer des données dans un fichier externe donnees.txt, situé dans le même dossier, à l'aide de la fonction programmation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Représentation graphique
Pour représenter graphiquement un nuage de points à l'aide de Python, le plus courant est d'utiliser la bibliothèque programmation.
Cette bibliothèque regroupe de très nombreuses fonctions utiles. On se propose ici de commenter l'exemple ci-dessous :
Bien d'autres fonctions de la bibliothèque matplotlib.pyplot sont à retrouver en .
❯ Programme Python permettant de récupérer des données dans un fichier externe de type .txt et de représenter graphiquement les positions et les vecteurs vitesse.

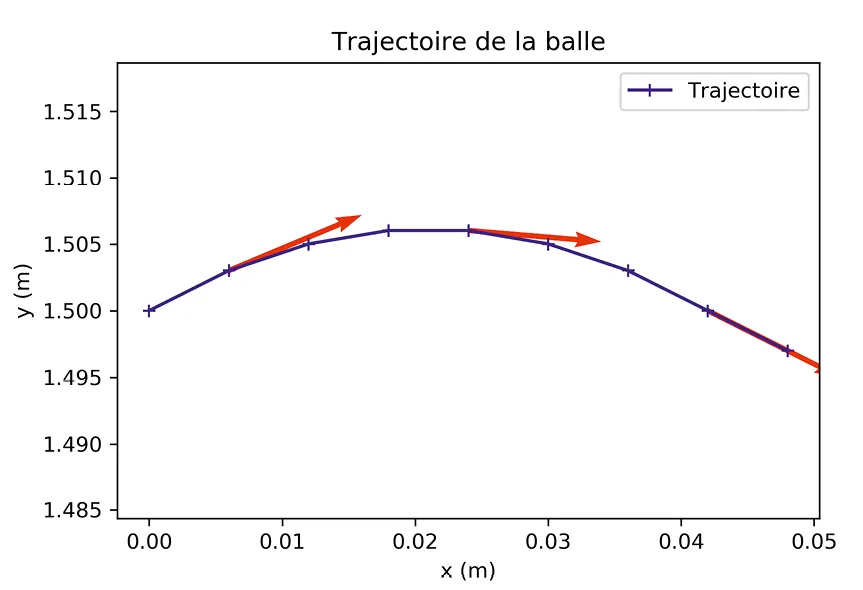
❯ La figure ci-dessus représente la trajectoire de la chute d'une balle avec matplotlib. Quelques vecteurs vitesse y sont représentés.
Cette bibliothèque regroupe de très nombreuses fonctions utiles. On se propose ici de commenter l'exemple ci-dessous :
- axis() : fonction permettant de paramétrer les axes du graphe (ici, le paramètre option est utilisé avec la valeur equal permettant d'avoir des axes orthonormés) ;
- title() : fonction permettant d'affecter et d'afficher un titre au graphe ;
- xlabel() et ylabel() : fonctions permettant d'affecter un titre aux axes ;
- plot() : fonction permettant de positionner des points dont les abscisses et les ordonnées proviennent des listes x et y (l'utilisation des paramètres color, label et marker permettent de personnaliser l'affichage des points) ;
- quiver() : fonction permettant de tracer des vecteurs avec pour paramètres les coordonnées du point d'origine x et y, les coordonnées du vecteur et divers paramètres utiles pour un affichage pertinent ;
- legend() : fonction permettant d'afficher la légende du graphe ;
- show() : fonction permettant d'afficher le graphe à l'écran.
Bien d'autres fonctions de la bibliothèque matplotlib.pyplot sont à retrouver en .
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
# Lecture des données du fichier txt
t, x, y = np.loadtxt('donnees.txt', unpack=True, usecols=(0, 1, 2), delimiter = '\t', skiprows = 2)
# Fonction de tracé des vecteurs vitesse
def vecteur_vitesse(x, y, t, i):
"""Création de la fonction permettant de tracer un vecteur vitesse au point Mi"""
vx = (x[i+1] - x[i-1])/(t[i+1] - t[i-1])
vy = (y[i+1] - y[i-1])/(t[i+1] - t[i-1])
plt.quiver(x[i], y[i], vx, vy, angles = "xy", scale_units = "xy", scale = 60, color = "red")
# Création du graphique
plt.axis('equal')
plt.title('Trajectoire de la balle')
plt.xlabel('x (m)')
plt.ylabel('y (m)')
plt.plot(x, y, color = 'blue', label = 'Trajectoire', marker = '+')
for i in range(1, len(t), 3) :
Vecteur_vitesse(x, y, t, i)
# Fin de la création du graphique
plt.legend()
plt.savefig('image.png', dpi=600)
plt.show()
❯ Programme Python permettant de récupérer des données dans un fichier externe de type .txt et de représenter graphiquement les positions et les vecteurs vitesse.


❯ La figure ci-dessus représente la trajectoire de la chute d'une balle avec matplotlib. Quelques vecteurs vitesse y sont représentés.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

