Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
1. Constitution et transformations de la matière
Ch. 1
Identification des espèces chimiques
Ch. 2
Composition des solutions aqueuses
Ch. 3
Dénombrer les entités
Ch. 4
Le noyau de l’atome
Ch. 5
Le cortège électronique
Ch. 6
Stabilité des entités chimiques
Ch. 7
Modélisation des transformations physiques
Ch. 8
Modélisation des transformations chimiques
Ch. 9
Synthèse de molécules naturelles
Ch. 10
Modélisation des transformations nucléaires
2. Mouvement et interactions
Ch. 11
Décrire un mouvement
Ch. 12
Modéliser une action sur un système
Ch. 13
Principe d’inertie
3. Ondes et signaux
Ch. 14
Émission et perception d’un son
Ch. 15
Analyse spectrale des ondes lumineuses
Ch. 16
Propagation des ondes lumineuses
Ch. 17
Signaux et capteurs
Méthode
Fiches méthode
Fiches méthode compétences
Annexes
Fiche méthode 4
Exclusivité numérique
Les angles
Télécharger la fiche au format PDF .15 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Exprimer un angle
❯
Mesure et unités
Un angle (noté \theta) s'exprime souvent en degrés (°) ou en radians (rad).
On utilise un rapporteur pour le mesurer.
Un angle (noté \theta) s'exprime souvent en degrés (°) ou en radians (rad).
On utilise un rapporteur pour le mesurer.
Le zoom est accessible dans la version Premium.
❯ Conversions d'unités
Un tour de cercle complet représente 360° ou 2 \pi \mathrm{rad}. On se sert de cette relation de proportionnalité pour convertir les mesures.
Exemple : L'angle mesuré ci-contre est de 35°.
Convertir cette mesure en radians : \theta(\mathrm{rad})=\dfrac{35 \times 2 \pi}{360}=0\text{,}61\, \mathrm{rad}
Un tour de cercle complet représente 360° ou 2 \pi \mathrm{rad}. On se sert de cette relation de proportionnalité pour convertir les mesures.
Exemple : L'angle mesuré ci-contre est de 35°.
Convertir cette mesure en radians : \theta(\mathrm{rad})=\dfrac{35 \times 2 \pi}{360}=0\text{,}61\, \mathrm{rad}
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Longueur d'un arc de cercle
❯ Angle quelconque
Le périmètre P du cercle mesure 2 \pi R et correspond à un angle \theta = 360°.
On se sert de la proportionnalité entre la longueur de l'arc et l'angle.
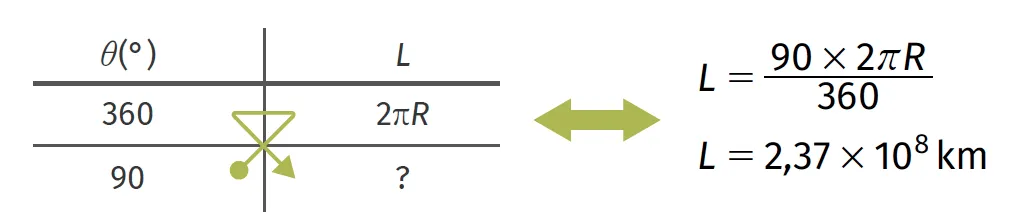
Exemple : Pour calculer la distance L parcourue par la Terre en 3 mois (¼ de tour de Soleil, donc un angle de 90°) : R=d_{\text {Terre-Soleil }}=150 \times 10^{6} km
Le périmètre P du cercle mesure 2 \pi R et correspond à un angle \theta = 360°.
On se sert de la proportionnalité entre la longueur de l'arc et l'angle.
Exemple : Pour calculer la distance L parcourue par la Terre en 3 mois (¼ de tour de Soleil, donc un angle de 90°) : R=d_{\text {Terre-Soleil }}=150 \times 10^{6} km
Le zoom est accessible dans la version Premium.
l = longueur du segment \text{[AB]}
L = longueur de l'arc
\theta = angle au centre délimitant l'arc \widehat{\mathrm{AB}}
Le zoom est accessible dans la version Premium.
❯ Si l'angle \theta est petit
L est alors très proche de l : on peut alors considérer que L = l.
Mesurer directement l à la règle par exemple.
L est alors très proche de l : on peut alors considérer que L = l.
Mesurer directement l à la règle par exemple.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Relations de trigonométrie
❯ Définitions
\cos (\theta)=\dfrac{\operatorname{adj}}{\operatorname{hyp}}=\dfrac{\mathrm{AC}}{\mathrm{AB}}
\sin (\theta)=\dfrac{\text { opp }}{\text { hyp }}=\dfrac{\mathrm{BC}}{\mathrm{AB}}
\tan (\theta)=\dfrac{\sin (\theta)}{\cos (\theta)}=\dfrac{\mathrm{opp}}{\mathrm{adj}}=\dfrac{\mathrm{BC}}{\mathrm{AC}}
Faire l'unité d'angle sur la calculatrice.
\cos (\theta)=\dfrac{\operatorname{adj}}{\operatorname{hyp}}=\dfrac{\mathrm{AC}}{\mathrm{AB}}
\sin (\theta)=\dfrac{\text { opp }}{\text { hyp }}=\dfrac{\mathrm{BC}}{\mathrm{AB}}
\tan (\theta)=\dfrac{\sin (\theta)}{\cos (\theta)}=\dfrac{\mathrm{opp}}{\mathrm{adj}}=\dfrac{\mathrm{BC}}{\mathrm{AC}}
Faire l'unité d'angle sur la calculatrice.
Le zoom est accessible dans la version Premium.
❯ Calculer l'angle à partir de la valeur du cosinus, du sinus ou de la tangente
Utiliser les fonction arccos (aussi écrit cos-1), arcsin (sin-1) ou arctan (tan-1) de la calculatrice (en couleur au dessus des touches cos, sin ou tan.
Accessibles avec la touche
Accessibles avec la touche
SHIFT
ou 2nde
.
Ex : Si \text{BC} = 4 cm et \text{AB} = 6 cm
\sin (\theta)=\dfrac{\mathrm{BC}}{\mathrm{AB}}=\dfrac{4}{6}=0\text{,}67
\theta=\sin ^{-1}(0\text{,}67)=42^{\circ}=0\text{,}73 rad
\sin (\theta)=\dfrac{\mathrm{BC}}{\mathrm{AB}}=\dfrac{4}{6}=0\text{,}67
\theta=\sin ^{-1}(0\text{,}67)=42^{\circ}=0\text{,}73 rad
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah