Mathématiques 4e - 2022
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algorithmique et programmation
Dossier Scratch
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d'équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Prolongement
Chapitre 5
Activités
Calcul littéral
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Naissance du calcul littéral
Dans son livre qui marque la naissance de l'algèbre, les équations présentées par Al-Khwarizmi au IXe siècle sont écrites en toutes lettres et forment des phrases ; les méthodes pour les résoudre sont géométriques. En cherchant à aller plus vite, les mathématiciens tentent alors de réduire ces phrases en utilisant des abréviations. Au XVIe siècle, tout s'accélère. Par exemple :
« le cube d'un nombre additionné de trois fois son carré égale 21 » est noté par Gerolamo Cardano « cubus & quadrata 3 aequantur 21 » et plus simplement encore par Rafael Bombelli \text{«~}
{\overset{3}{\breve1}~p.~\overset{2}{\breve3}~a~21}\text{~»}.
Bien que les symboles + et - soient utilisés entre des nombres un siècle plus tôt par Johannes Widmann, les mathématiciens Christoff Rudolff et Michael Stifel ont été les premiers à les utiliser entre des lettres qui indiquent des grandeurs inconnues. Quant au symbole =, il a été introduit par le mathématicien Robert Recorde. À la fin du XVIe siècle, c'est à François Viète que l'on doit l'utilisation systématique de lettres pour indiquer des grandeurs inconnues mais aussi leurs coefficients, ce qui permet dans une même écriture d'avoir des inconnues différentes et de faire des opérations algébriques sur ces lettres. C'est enfin grâce aux évolutions données par René Descartes au XVIIe siècle que se mettent en place les notations que nous utilisons encore. Il aurait écrit notre équation initiale : x^{3}+3 x x\propto 21. Des écritures littérales se détachent alors des objets concrets qu'elles représentent et l'algèbre se développe de façon autonome.


Écrire l'équation {\boldsymbol{x^{2}+4=10}} à la manière de Gerolamo Cardano puis de Rafael Bombelli.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Un bracelet et des perles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Éléana souhaite fabriquer un bracelet en alternant des perles cubiques et des perles rondes. Elle commence et termine son bracelet avec des perles rondes. De plus, chaque perle cubique est incrustée de quatre perles rondes.
1
Si elle utilise deux perles cubiques, justifier qu'il y aura onze perles rondes sur son bracelet.2
Même question avec trois perles cubiques, cinq perles cubiques et vingt perles cubiques.
3
Si l'on note x le nombre de perles cubiques, déterminer, en fonction de x, le nombre de perles rondes utilisées puis calculer le nombre de perles rondes nécessaires avec 25 perles cubiques.Bilan
Pourquoi est-il préférable d'utiliser une expression littérale pour déterminer le nombre de perles rondes dans ce bracelet ?Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2Gagner de la place
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
On rappelle que {1x = x}.a) Expliquer rapidement pourquoi x+x+x+x=4 \times x.
2
La capture d'écran suivante vient du logiciel GeoGebra.
Proposer une méthode de calcul pouvant expliquer les résultats obtenus en gras.

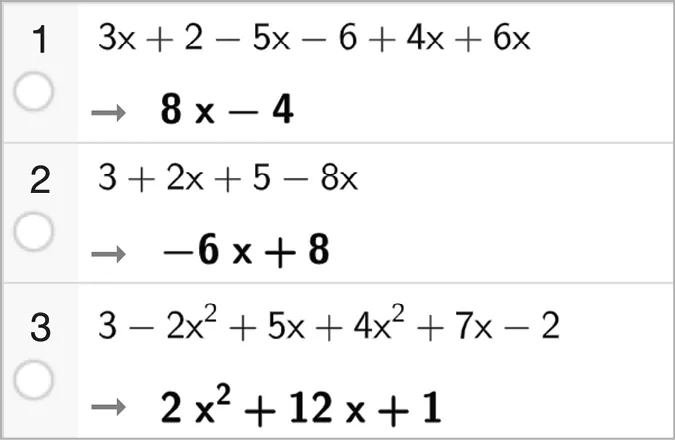
Bilan
Comment faire pour réduire une expression littérale ? Donner un intérêt.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 3La distributivité dans un rectangle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On considère le rectangle \text{ABCD} suivant. Les points \text{E} et \text{F} sont placés comme sur la figure de telle sorte que \text{DAFE} et \text{EFBC} soient des rectangles. k, a et b représentent les longueurs respectives des segments \text{[AD]}, \text{[AF]} et \text{[FB]}.
On en déduit que k, a et b sont des nombres strictement positifs.

On en déduit que k, a et b sont des nombres strictement positifs.

1
Calculer l'aire du rectangle \text{ABCD} lorsque {k = 4\text{~cm}}, {a = 3\text{~cm}} et {b = 6\text{~cm}}.Coup de pouce
On rappelle que la formule pour calculer l'aire d'un rectangle est \text{L} \times \ell.
2
Même question avec {k = 3\text{~cm}}, {a = 2\text{~cm}} et {b = 5\text{~cm}}.
3
Dans cette question, on ne connaît pas les valeurs de k, a et b. Exprimer de deux façons différentes l'aire du rectangle \text{ABCD} en utilisant les lettres k, a et b.
Bilan
En utilisant les questions précédentes, compléter l'égalité suivante pour tous nombres strictement positifs k, a et b : k \times(a+b)= Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
