Mathématiques Expertes Terminale
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 4
Synthèse
Exercices de synthèse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
112
Python
[Calculer, Communiquer.]
D'après bac S, Polynésie, juin 2014
Un magicien propose le tour suivant : « Multipliez par 12 le numéro de votre jour de naissance. Ajoutez à ce résultat le numéro de votre mois de naissance multiplié par 31. Je vais deviner votre date de naissance ».
Un magicien propose le tour suivant : « Multipliez par 12 le numéro de votre jour de naissance. Ajoutez à ce résultat le numéro de votre mois de naissance multiplié par 31. Je vais deviner votre date de naissance ».


1. Résoudre dans \mathbb{Z}^2 l'équation (\text E_0) : 12\text X = 31 \text Y.
2. Déterminer une solution particulière dans \mathbb{Z}^2 de
l'équation (\text E_1) : 12 x + 31 y = 1.
3. En déduire une solution particulière (x_0 \, ; y_0) \in \mathbb{Z}^2 de
l'équation (\text E) : 12x + 31y = 503.
4. Montrer que si (x \, ; y) \in \mathbb{Z}^2 est solution de l'équation
(\text E), alors le couple (x-x_0\, ; y_0-y) est solution de (\text E_0). En déduire l'ensemble des solutions de (\text E).
5. Justifier que (\text E) admet une unique solution vérifiant 1 \leqslant y \leqslant 12 et la déterminer. Quelle est la date de naissance d'une personne obtenant 503 ?
6. a. On considère l'algorithme suivant.
Modifier cet algorithme afin qu'il prenne en argument un nombre entier m et retourne les valeurs de x et de y telles que 12x + 31y = m et 1 \leqslant y \leqslant 12.
\boxed{
\begin{array} { l } { \text {Pour} \ x \ \text{allant de 1 à 31 faire : }} \\
\quad \text {Pour}\ y\ \text{allant de 1 à 12 faire : }\\
\quad \quad z \leftarrow {12 x + 31 y}\\
\quad \quad \text {Afficher } z \\
\quad \text {Fin Pour} \\
\text {Fin Pour} \\
\end{array}
}
Modifier cet algorithme afin qu'il prenne en argument un nombre entier m et retourne les valeurs de x et de y telles que 12x + 31y = m et 1 \leqslant y \leqslant 12.
b. Programmer et exécuter cet algorithme afin de déterminer
la date de naissance d'une personne qui obtient 355.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
113
[Calculer, Raisonner.]
Soit n un entier naturel tel que n \equiv 9[17] et n \equiv 3[5].
1. Montrer qu'il existe un couple (u \, ; v) \in \mathbb{Z}^2 tel que n = 17u + 9, n = 5v + 3 et 5v - 17u = 6.
2. Justifier que l'équation 5v - 17u = 6 admet des solutions entières et en déterminer une.
2. Justifier que l'équation 5v - 17u = 6 admet des solutions entières et en déterminer une.
3. En déduire l'ensemble des solutions de l'équation
5v - 17u = 6 puis en déduire que n \in \{43 + 85k, k \in \mathbb{Z} \}.
4. Montrer que, pour tout entier relatif k, 43 + 85k est solution du problème. Conclure.
4. Montrer que, pour tout entier relatif k, 43 + 85k est solution du problème. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
114
Démo
[Communiquer, Raisonner.]
Soient a et b deux entiers relatifs non nuls. On pose d = \text{PGCD}(a \, ; b). 1. On considère deux entiers u et v tels que au + bv = 1.
a. Justifier que d divise au + bv.
b. En déduire alors que a et b sont premiers entre eux.
Justifier que l'ensemble \text{E} n'est pas vide ; autrement dit qu'il existe un entier k > 0 tel que au + bv = k.
On admet pour toute la suite que \text E admet un plus petit élément noté c.
3. a. Écrire la division euclidienne de a par c en notant
q le quotient et r le reste.
b. Justifier qu'il existe deux entiers \text{U} et \text{V} tels que r = a\text U + b\text V et en déduire que si r > 0, alors r \in \text E.
c. En déduire alors que r = 0 et donc que c | a.
b. Justifier qu'il existe deux entiers \text{U} et \text{V} tels que r = a\text U + b\text V et en déduire que si r > 0, alors r \in \text E.
c. En déduire alors que r = 0 et donc que c | a.
4. a. Démontrer que c | b.
b. En déduire alors que c = 1.
c. Conclure en rédigeant intégralement la propriété démontrée par les questions 2. à 4..
b. En déduire alors que c = 1.
c. Conclure en rédigeant intégralement la propriété démontrée par les questions 2. à 4..
5. Quelle équivalence cet exercice a-il permis de
démontrer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
115
[Calculer, Chercher.]
Théorème des restes chinois




Dix‑sept pirates ont gagné un gros butin. Ils comptent
qu'en prenant tous la même part, il reste trois pièces
pour le cuisinier chinois.
Un soir, une mutinerie éclate au cours de laquelle six pirates sont tués. Ils comptent alors qu'en se répartissant le butin, il reste quatre pièces pour le cuisinier.
Or, avant qu'ils aient distribué cet argent, cinq autres membres meurent du scorbut. Le cuisinier chinois compte alors qu'en donnant la même somme à chaque pirate restant, il lui reviendra cinq pièces.
On cherche à déterminer de combien de pièces est constitué ce butin.
Un soir, une mutinerie éclate au cours de laquelle six pirates sont tués. Ils comptent alors qu'en se répartissant le butin, il reste quatre pièces pour le cuisinier.
Or, avant qu'ils aient distribué cet argent, cinq autres membres meurent du scorbut. Le cuisinier chinois compte alors qu'en donnant la même somme à chaque pirate restant, il lui reviendra cinq pièces.
On cherche à déterminer de combien de pièces est constitué ce butin.
1. Soit b le butin des pirates. Traduire l'énoncé par un
système de trois congruences.
2. À la fin, chaque pirate a 84 pièces de plus que dans le premier partage. Montrer que si b \in \mathbb{N} est une solution du système, alors il existe trois entiers naturels x, y et z tels que 17x - 11y = 1, 11y - 6z = 1 et z - x = 84.
3. Déterminer l'ensemble des solutions de chacune des deux premières équations.
2. À la fin, chaque pirate a 84 pièces de plus que dans le premier partage. Montrer que si b \in \mathbb{N} est une solution du système, alors il existe trois entiers naturels x, y et z tels que 17x - 11y = 1, 11y - 6z = 1 et z - x = 84.
3. Déterminer l'ensemble des solutions de chacune des deux premières équations.
4. En utilisant l'équation z - x = 84, donner la relation entre les deux paramètres définissant les solutions des
équations 17x - 11y = 1 et 11y - 6z = 1.
5. En déduire la valeur de ces paramètres, puis la solution du problème.
5. En déduire la valeur de ces paramètres, puis la solution du problème.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
116
[Calculer, Chercher.]
Chiffrement
1. a. Déterminer un entier u_0 tel que 5u_0 \equiv 1[28].
b. Soient u et v deux entiers tels que 5u + 28v = 1.
Montrer que 5u-5u_0 \equiv 0[28] et en déduire les valeurs de u et v telles que u \in \{0 \,; ... \,; 28\}.
b. Soient u et v deux entiers tels que 5u + 28v = 1.
Montrer que 5u-5u_0 \equiv 0[28] et en déduire les valeurs de u et v telles que u \in \{0 \,; ... \,; 28\}.
2. On chiffre un message de la manière suivante : à chaque lettre est associé un entier entre 0 et 25 en suivant l'ordre alphabétique.
Un entier n \in \{0 \,; ... \,; 25\} sera codé par l'unique entier m \in \{0 ; ... ; 28\} tel que m \equiv n^5 [29].
a. Soient n \in \{0 \,; ... \,; 25\} et m \in \{0 \,; ... \,; 28\} la version chiffrée de n. Montrer que m^{17} \equiv n \times n^{28\times3}[29].
b. On admet que n^{28} \equiv 1 [29].
Déduire de ce qui précède que la fonction de décodage consiste à calculer le reste de la division euclidienne de m^{17} par 29.
Un entier n \in \{0 \,; ... \,; 25\} sera codé par l'unique entier m \in \{0 ; ... ; 28\} tel que m \equiv n^5 [29].
a. Soient n \in \{0 \,; ... \,; 25\} et m \in \{0 \,; ... \,; 28\} la version chiffrée de n. Montrer que m^{17} \equiv n \times n^{28\times3}[29].
b. On admet que n^{28} \equiv 1 [29].
Déduire de ce qui précède que la fonction de décodage consiste à calculer le reste de la division euclidienne de m^{17} par 29.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
117
Devoir maison
[Communiquer, Modéliser.]


Un distributeur de pièces ne dispose que de deux
sortes de pièces de montants a et b, où a et b sont des entiers naturels non nuls. Pour distribuer une somme \text S,
il doit trouver une combinaison linéaire à coefficients
entiers positifs de a et b.
1. On suppose que a = 2 et que b est un entier impair
supérieur ou égal à 3.
a. Montrer que le distributeur peut payer toutes les sommes paires.
Soient \text S \geqslant b un entier naturel impair et respectivement q et r le quotient et le reste de la division euclidienne de \text{S} par b.
a. Montrer que le distributeur peut payer toutes les sommes paires.
Soient \text S \geqslant b un entier naturel impair et respectivement q et r le quotient et le reste de la division euclidienne de \text{S} par b.
b. Montrer que si q est impair, alors r est pair, et que
si q est pair, alors b + r est pair. En déduire que le
distributeur peut payer toutes les sommes supérieures
ou égales à b.
\boxed{
\begin{array} { l } \text {Demander S} \\
q \leftarrow \text E(\text S/b) \\
r \leftarrow \text S - b \times q \\
\text {Si } q \text { est impair : } \\
\quad \quad \begin{cases}
n_a= ...\\
n_b=... \\
\text S = ...
\end{cases}\\
\text{Sinon :}\\
\quad \quad\begin{cases}
n_a=...\\
n_b=...\\
\text S=...
\end{cases}
\end{array}
}
On souhaite montrer qu'on ne peut pas payer la somme ab - a - b.
Supposons donc par l'absurde qu'il existe (x \,; y) \in \mathbb{N}^2 tel que ax + by = ab - a - b.
a. Montrer qu'il existe alors k \in \mathbb{Z} tel que x + 1 = kb.
b. En déduire que y = a - 1 - ak.
c. Montrer que l'égalité x + 1 = kb implique que k > 0 et que l'égalité y = a - 1 - ak implique que k \lt 1.
d. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
118
[Calculer, Raisonner.]
Soit (a \,; b) un couple d'entiers strictement positifs tels que a^2 = b^3. On note d = \text{PGCD}(a \,; b). Soient x et y les entiers tels que a = dx et b = dy.
1. Montrer le lemme suivant : « Pour tous entiers x et y premiers entre eux, y \vert x^2 \Rightarrow y \vert x. »
2. Montrer que x^2 = dy^3.
3. Justifier que y \vert x et en déduire que y = 1.
4. En déduire que a et b sont respectivement le cube et le carré d'un même entier.
5. Soit x un entier naturel non nul.
a. Quels sont les restes possibles dans la division euclidienne de x^2 par 7 ? Et de x^6 par 7 ?
b. En déduire que si n est le carré d'un entier et le cube d'un autre entier, alors n \equiv 0[7] ou n \equiv 1[7].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
119
[Calculer, Chercher.]
Une jeune fille portait des œufs pour les vendre au marché. Elle rencontra un jeune homme qui voulut jouer avec elle et qui cassa tous ses œufs sans les lui rembourser.
Le juge condamna le jeune homme à payer les œufs. Mais le juge ne savait pas combien il y en avait et le demanda à la jeune fille.
Elle prétendit ne pas les avoir comptés, mais qu'elle avait essayé de les ranger par 2 et qu'il restait 1 oeuf, puis par 3 et qu'il en restait encore 1, puis par 4, par 5 et par 6 et que, dans chaque cas, il en restait 1 et enfin par 7 et que cette fois il n'y avait pas d'œuf en reste.
1. Traduire cet énoncé par un système de congruences.
2. En déduire que le nombre d'œufs n vérifie n \equiv 1[60] et n \equiv 0[7].
3. En déduire qu'il existe des entiers a et b tels que n = 7a = 60b + 1 et déterminer l'ensemble des couples (a \,; b) d'entiers vérifiant 7a = 60b + 1.
4. En déduire le plus petit nombre d'œufs possible de la jeune fille.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
120
Un problème chinois
Le problème des cent volailles a été énoncé au Ve siècle
en Chin : « Un coq vaut cinq pièces, une poule trois
pièces et trois poussins valent une pièce. Avec cent
pièces, on achète cent volailles. Combien y a‑t‑il de
coqs, de poules et de poussins ? »
L'auteur donne une méthode pour trouver toutes les solutions à partir d'une solution particulière : accroître les coqs chaque fois par 4, décroître les poules chaque fois par 7 et accroître les poussins chaque fois par 3.
L'auteur donne une méthode pour trouver toutes les solutions à partir d'une solution particulière : accroître les coqs chaque fois par 4, décroître les poules chaque fois par 7 et accroître les poussins chaque fois par 3.
1. Soient x le nombre de coqs, y le nombre de poules et
z le nombre de poussins.
Montrer que (x \, ; y \,; z) vérifie \begin{cases} z = 100 - x - y \\ 14 x + 8y = 200 \end{cases}.
Montrer que (x \, ; y \,; z) vérifie \begin{cases} z = 100 - x - y \\ 14 x + 8y = 200 \end{cases}.
a. Montrer que 7(x-x_0)=4(y_0-y) et en déduire les
expressions de x et y en fonction de x_0 et y_0. Vérifier que cela confirme la méthode donnée.
b. Justifier que le nombre de poussins augmente de 3
entre chaque triplet solution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
121
Racines rationnelles d'un polynôme
Partie A : Étude d'un cas particulier
Le but est de déterminer les éventuelles solutions rationnelles de l'équation polynomiale 15x^3 - 7x + 3 = 0.
Le but est de déterminer les éventuelles solutions rationnelles de l'équation polynomiale 15x^3 - 7x + 3 = 0.
1. a. Soit x \in \mathbb{Z}.
Que peut‑on dire du \text{PGCD} de x et x^3 ?
Que peut‑on dire du \text{PGCD} de x et x^3 ?
b. Supposons qu'il existe une solution entière x.
Justifier que x ne peut valoir que -3 ; -1 ; 1 ou 3.
c. Conclure sur l'existence de solutions entières.
a. Montrer que 15p^3 - 7pq^2 = -3q^3.
b. En appliquant le théorème de Gauss, démontrer que
p divise 3.
c. De même, montrer que q divise 15p^3, puis que q
divise 15.
d. En déduire les valeurs positives possibles de
\dfrac{p}{q}.
Sont‑elles solutions ?
1. Soient a, b et c trois entiers naturels non nuls. Montrer que pour tout n \in \mathbb{N}, si c \vert a \times b^n et \text{PGCD}(b\,;c) = 1, alors c \vert a.
2. On considère l'équation polynomiale à coefficients entiers a_5x^5+a_4x^4+a_3x^3+a_2x^2+a_1x+a_0=0.
Soit (p \, ; q) \in \mathbb{Z}^2 avec q \neq 0 tel que \dfrac{p}{q} soit solution de cette équation avec \text{PGCD}(p\, ; q)= 1.
a. Montrer que : a_5p^5+a_4p^4q+a_3p^3q^2+a_2p^2q^3+a_1pq^4=-a_0q^5.
En déduire que p divise a_0.
En déduire que p divise a_0.
b. De même, montrer que q divise a_5.
a. Déduire de ce qui précède que l'ensemble des
rationnels non entiers solutions de l'équation 2x^5+41x^4-7x-6=0 est inclus dans \left\{\dfrac{1}{2}\, ; \dfrac{-1}{2} \, ; \dfrac{3}{2} \, ; \dfrac{-3}{2}\right\}.
b. En déduire l'ensemble des solutions rationnelles de
cette équation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
122
Triplets pythagoriciens
Un triplet pythagoricien est un triplet (x \,; y \,; z) d'entiers naturels non nuls tels que x^2 + y^2 = z^2 (\text E).
1. Peut‑il y avoir des solutions si z = 1 ou z = 2 ?
2. Supposons que z > 2 et que (x \,; y \,; z) est un triplet pythagoricien.
Que peut‑on dire du \text{PGCD} de x et y ?
3. Montrer que si x et y ont la même parité, alors z est pair, et que s'ils sont de parités différentes, alors z est impair.
4. On suppose dans la suite que x est pair.
Soit x' tel que x = 2x'.
Vérifier que 4x'^2 = (z - y)(z + y).
5. Justifier que z - y et z + y sont pairs et montrer que si \text{PGCD}(y \, ; z) = 1, alors \text{PGCD} \left(\dfrac{z-y}{2} \, ; \dfrac{z+y}{2} \right) = 1.
6. On suppose dans la suite de l'exercice que \text{PGCD}(y \, ; z) = 1.
On admet le lemme suivant : « Soient a, b, c trois entiers naturels tels que \text{PGCD}(a \,; b) = 1 et ab = c^2. Alors il existe deux entiers relatifs u et v premiers entre eux tels que a = u^2 et b = v^2. »
En déduire qu'il existe deux entiers relatifs premiers entre eux tels que \dfrac{z-y}{2} = u^2 et \dfrac{z+y}{2}=v^2.
2. Supposons que z > 2 et que (x \,; y \,; z) est un triplet pythagoricien.
Que peut‑on dire du \text{PGCD} de x et y ?
3. Montrer que si x et y ont la même parité, alors z est pair, et que s'ils sont de parités différentes, alors z est impair.
4. On suppose dans la suite que x est pair.
Soit x' tel que x = 2x'.
Vérifier que 4x'^2 = (z - y)(z + y).
5. Justifier que z - y et z + y sont pairs et montrer que si \text{PGCD}(y \, ; z) = 1, alors \text{PGCD} \left(\dfrac{z-y}{2} \, ; \dfrac{z+y}{2} \right) = 1.
6. On suppose dans la suite de l'exercice que \text{PGCD}(y \, ; z) = 1.
On admet le lemme suivant : « Soient a, b, c trois entiers naturels tels que \text{PGCD}(a \,; b) = 1 et ab = c^2. Alors il existe deux entiers relatifs u et v premiers entre eux tels que a = u^2 et b = v^2. »
En déduire qu'il existe deux entiers relatifs premiers entre eux tels que \dfrac{z-y}{2} = u^2 et \dfrac{z+y}{2}=v^2.
7. En déduire que z est la somme des carrés de deux
entiers, et exprimer x et y en fonction de ces entiers.
8. Application : Les équations x^2 + y^2 = 25 et x^2 + y^2 = 49 admettent-elles des solutions ?

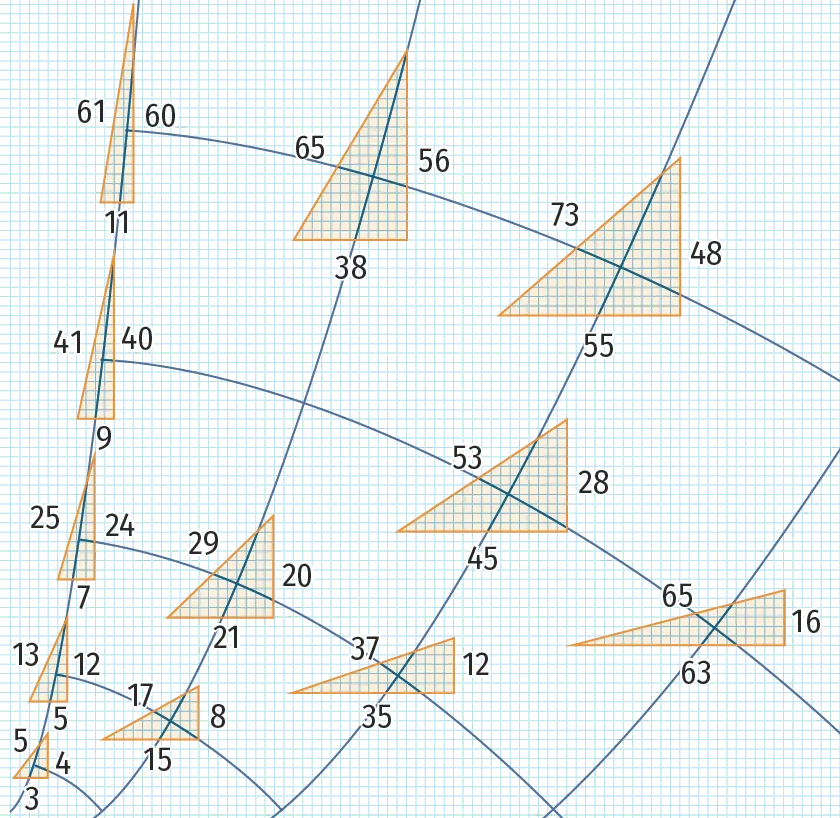
Exemples de triplets pythagoriciens représentés par des triangles rectangles.
8. Application : Les équations x^2 + y^2 = 25 et x^2 + y^2 = 49 admettent-elles des solutions ?


Exemples de triplets pythagoriciens représentés par des triangles rectangles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
123
Casse-tête
Un jour, dans une auberge, s'arrête un groupe de voyageurs. Des hommes, mais aussi des femmes, en moindre nombre mais tout autant affamées, s'attablent. Il est convenu à l'issue du repas que les hommes paieront chacun 19 sous et les femmes 13 sous chacune. L'aubergiste récolte ainsi exactement 1 000 sous.
Combien y avait‑il d'hommes et de femmes dans ce groupe ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
124
Défi
Un triangle pythagoricien est un triangle rectangle dont
les trois côtés ont des mesures entières.
Le triangle de mesures 3, 4 et 5 est par exemple un triangle pythagoricien.
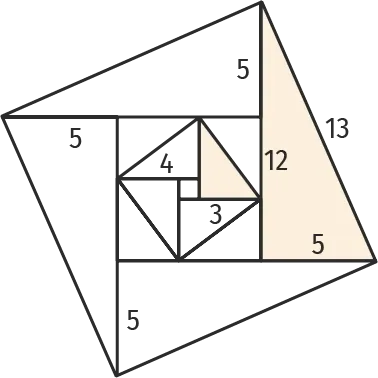
Déterminer les 20 triplets pythagoriciens qu'on obtiendrait si on construisait les triangles successifs comme sur le schéma ci-dessous.
Le petit côté du triangle augmente toujours de 2.
Le tout petit carré central a pour côté \color{black}1. Quel est le côté du carré au centre de la 2e série de triangles ?
Le triangle de mesures 3, 4 et 5 est par exemple un triangle pythagoricien.
Déterminer les 20 triplets pythagoriciens qu'on obtiendrait si on construisait les triangles successifs comme sur le schéma ci-dessous.
Aide

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le Grand Oral
Entraînez-vous au Grand Oral et enregistrez-vous sur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Comme le suggère le programme, les problèmes abordés en maths expertes peuvent servir d'appui à des questions de Grand Oral. Voici un exemple, basé sur l'enseignement de spécialité, utilisant des notions de ce chapitre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans le cadre de l'enseignement de spécialité, vous avez étudié le théorème des valeurs intermédiaires.
1. Citer ce théorème en précisant ses hypothèses de validité.
2. a. Utiliser ce théorème pour montrer que l'équation 8x^3 + 15x^2 + 22x - 3 = 0 admet une unique solution \alpha sur \mathbb{R}.
b. Quelle méthode connaissez-vous pour obtenir une approximation de la valeur de la solution \alpha ?
2. a. Utiliser ce théorème pour montrer que l'équation 8x^3 + 15x^2 + 22x - 3 = 0 admet une unique solution \alpha sur \mathbb{R}.
b. Quelle méthode connaissez-vous pour obtenir une approximation de la valeur de la solution \alpha ?
3. Expliquer en quoi les méthodes du chapitre permettent de déterminer les éventuelles solutions rationnelles de l'équation 8x^3 + 15x^2 + 22x - 3 = 0. Quelle valeur de la solution obtient‑on ?
4. Citer des exemples de situations concrètes faisant intervenir une équation de cette forme.
4. Citer des exemples de situations concrètes faisant intervenir une équation de cette forme.
Méthodologie
Consulter les fiches méthode de ce manuel pour le
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
