Quelle condition la longueur c du côté d'un carreau doit-elle vérifier pour que les carreaux remplissent la surface sans qu'on ait besoin de les couper ?

Soient a et b deux entiers naturels non nuls avec a > b.
a) Montrer que les diviseurs communs à a et b sont exactement les diviseurs communs à b et r, où r désigne le reste de la division euclidienne de a par b.

Aide

Écrire la division euclidienne de a par b : elle permet d'écrire r comme combinaison linéaire de a et b.

b) On appelle \text{PGCD} de a et b le plus grand diviseur commun de a et b.
En déduire que le \text{PGCD} de a et b est égal au \text{PGCD} de b et r.

Pour tout réel x, on note \text{E}(x) la partie entière de x, l'unique entier tel que \text{E}(x) \leqslant x \lt \text{E}(x) + 1. On considère l'algorithme suivant.

\begin{array}{|l|l|} \hline \text { 1. } & a \leftarrow 250 \\ \text { 2. } & b \leftarrow 70 \\ \text { 3. } & r \leftarrow 250-70 \times \mathrm{E}\left(\frac{250}{70}\right) \\ \text { 4. } & \text { Tant que } r \neq 0 \text { faire : } \\ \text { 5. } & a \leftarrow b \\ \text { 6. } & b \leftarrow r \\ \text { 7. } & r \leftarrow a-b \times \mathrm{E}\left(\frac{a}{b}\right) \\ \text { 8. } & \text { Fin Tant que } \\ \text { 9. } & \text { Afficher } b \\ \hline \end{array}

a) À quoi les nombres 250-70 \times E\left(\frac{250}{70}\right) et a-b \times \mathrm{E}\left(\frac{a}{b}\right) (lignes 3 et 7) correspondent-ils ?

b) Exécuter cet algorithme à la main en recopiant et complétant le tableau suivant.

\boldsymbol{\color{white}a}	250
\boldsymbol{\color{white}b}	70
\boldsymbol{\color{white}r}

c) Pourquoi peut-on être sûr, sans l'exécuter, que cet algorithme se termine nécessairement ?

d) Que représente le nombre affiché en sortie ?
Que peut-on déduire sur les dimensions possibles du pavage ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Bilan

Cet algorithme de divisions successives porte aujourd'hui le nom d'Euclide. Euclide a en réalité décrit un algorithme voisin dans son livre Les Éléments pour expliciter une méthode de détermination du \mathbf{PGCD} de deux entiers naturels non nuls.

Soient \boldsymbol{a} et \boldsymbol{b} deux entiers naturels non nuls. Expliquer comment on peut déterminer l'ensemble des diviseurs communs à \boldsymbol{a} et \boldsymbol{b} connaissant leur \mathbf{PGCD}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Un problème de Bachet

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Objectif : Utiliser le théorème de Bézout en « remontant » l'algorithme d'Euclide.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Deux bons compagnons ont 8 pintes de vin à partager entre eux également, lesquelles sont dans un vase contenant justement 8 pintes, et pour faire leur partage ils n'ont que deux autres vases dont l'un contient 5 pintes et l'autre 3. On demande comment ils pourront partager justement leur vin, ne se servant que de ces trois vases.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Remarque

Une pinte est une unité de mesure d'un volume.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Ce problème est posé par Bachet de Méziriac (1581-1638) dans Problèmes plaisants et délectables (1612). L'énoncé ci-dessus est tiré d'une réédition commentée de 1874. Une des méthodes qu'il donne consiste à remplir le vase \text{V}_5 (de cinq pintes) et à le vider dans le vase \text{V}_3 (de trois pintes) et ce jusqu'à obtenir une quantité de quatre pintes dans l'un des vases.
Le problème revient donc à déterminer combien de fois il faut remplir entièrement \text{V}_5 et combien de fois il faut lui retirer trois pintes pour qu'il contienne quatre pintes.

Écrire le problème sous la forme mx-py=4 avec (m \ ; \ p ) \in \N^2 et déterminer un couple (x \ ; \ y ) solution.

Bachet raisonne en prenant le problème par la fin : quatre pintes, ce sont cinq pintes dont on a retiré une pinte. Comment retirer une pinte ? Il suffit par exemple que le vase de trois pintes en contienne déjà deux.
a) Comment mesurer un volume de deux pintes avec les vases \text{V}_3 et \text{V}_5 ?

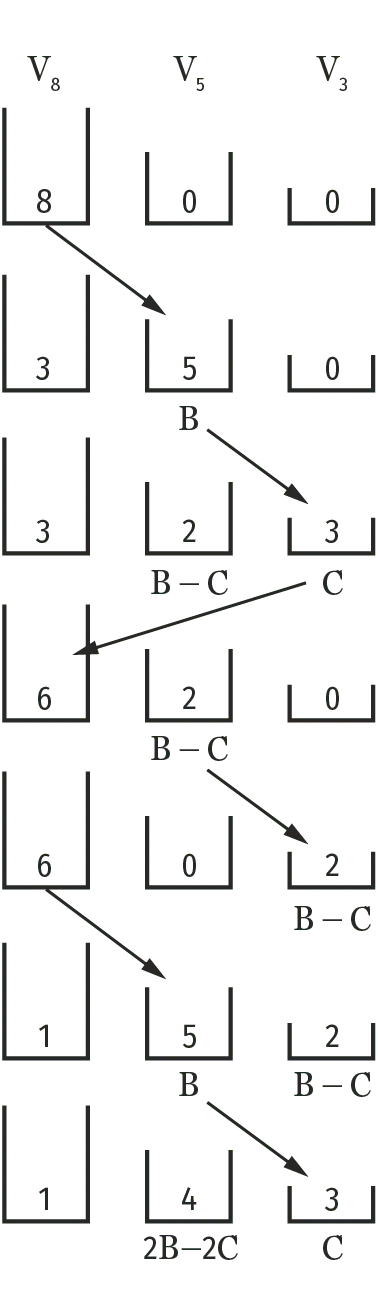
b) Observer le schéma suivant et expliquer pourquoi à la fin du processus le vase \text{V}_5 contient un volume de 2\text{B}-2 \text{C}.

Cherchons maintenant à obtenir un volume de une pinte avec des vases de seize et neuf pintes.
a) Écrire l'algorithme d'Euclide pour déterminer le \text{PGCD} de 16 et 9.

Soient r_1 et r_2 les restes des deux premières divisions euclidiennes obtenues.

b) À l'aide de la troisième division euclidienne, écrire le nombre 1 comme combinaison linéaire de r_1 et r_2.

c) À l'aide de la deuxième division euclidienne, écrire le nombre 2 comme combinaison linéaire de 9 et r_1, puis justifier comment obtenir 1 = 7 \times 4 - 3 \times 9.

d) En déduire une combinaison linéaire de 9 et 16 égale à 1. Conclure.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Bilan

Le théorème de Bézout indique que si le \mathbf{PGCD} de deux entiers naturels \boldsymbol{a} et \boldsymbol{b} est \boldsymbol{1}, alors il existe un couple d'entiers relatifs \boldsymbol{( u \ ; \ v)} tel que \boldsymbol{au + bv = 1}.
En prenant \boldsymbol{a = 12} et \boldsymbol{b = 5} et en s'appuyant sur le raisonnement de la question
3
, expliciter une démarche permettant de trouver \boldsymbol{u} et \boldsymbol{v} tels que \boldsymbol{12 u + 5v = 1}. Ce couple est-il unique ?

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

PGCD et applications

AProblème de pavage

BUn problème de Bachet

Remarque

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

A
Problème de pavage

B
Un problème de Bachet