Mathématiques Expertes Terminale
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres complexes
Ch. 1
Nombres complexes, point de vue algébrique
Ch. 2
Nombres complexes, point de vue géométrique
Arithmétique
Ch. 3
Divisibilité dans Z
Ch. 4
PGCD et applications
Ch. 5
Nombres premiers
Graphes et matrices
Ch. 6
Calcul matriciel et applications aux graphes
Ch. 7
Suites et matrices
Annexes
Cahier d'algorithmique et de programmation
Chapitre 4
TP / TICE 2
Établir un calendrier
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans le calendrier julien, les années sont divisées en 365 jours et on ajoute un jour tous les quatre ans (années bissextiles). Cependant, ce calendrier entraîne un décalage non négligeable avec le comportement des astres sur plusieurs siècles.
Questions préliminaires :
On estime qu'une année est composée de 365,2422 jours. On pose \text{A} = 365 + \dfrac{2~422}{10~000}.
Le choix optimal serait donc de rajouter 2~422 jours sur chaque période de 10~000 ans.
Pour obtenir une méthode plus pratique, on écrit le développement en fractions continues de \text{A} : on pose \text{q}_0 = 365, \text{r}_0 = 10~000 et \text{r}_1 = 2~422 et on définit, par divisions euclidiennes successives, les suites d'entiers (q_n) et (r_n) telles que, pour tout n \geqslant 1, r_{n-1} = r_n \times q_n + r_{n+1} et 0 \leqslant r_{n+1} < r_n.
Pour finir, on définit la suite (\text{A}_n), pour tout entier naturel n, par \text{A}_0 = q_0 + \dfrac{1}{q_1}, \text{A}_1 = q_0 + \dfrac{1}{q_1 + \dfrac{1}{q_2}} , etc.
Les termes \text{A}_n sont appelés développement en fractions continues.
On estime qu'une année est composée de 365,2422 jours. On pose \text{A} = 365 + \dfrac{2~422}{10~000}.
Le choix optimal serait donc de rajouter 2~422 jours sur chaque période de 10~000 ans.
Pour obtenir une méthode plus pratique, on écrit le développement en fractions continues de \text{A} : on pose \text{q}_0 = 365, \text{r}_0 = 10~000 et \text{r}_1 = 2~422 et on définit, par divisions euclidiennes successives, les suites d'entiers (q_n) et (r_n) telles que, pour tout n \geqslant 1, r_{n-1} = r_n \times q_n + r_{n+1} et 0 \leqslant r_{n+1} < r_n.
Pour finir, on définit la suite (\text{A}_n), pour tout entier naturel n, par \text{A}_0 = q_0 + \dfrac{1}{q_1}, \text{A}_1 = q_0 + \dfrac{1}{q_1 + \dfrac{1}{q_2}} , etc.
Les termes \text{A}_n sont appelés développement en fractions continues.
1.
a. Vérifier que q_1 = 4 et r_2 = 312 et en déduire la valeur de \text{A}_0.
b. Déterminer q_2 et en déduire une valeur approchée de \text{A}_1 à 10^{-2} près.
2. a. Justifier alors le choix du calendrier julien.
b. Quelle est l'erreur commise chaque année avec cette méthode ? Chaque siècle ?
c. Les années multiples de 4 sont‑elles toutes bissextiles ? Comment justifier ce choix ?
b. Déterminer q_2 et en déduire une valeur approchée de \text{A}_1 à 10^{-2} près.
2. a. Justifier alors le choix du calendrier julien.
b. Quelle est l'erreur commise chaque année avec cette méthode ? Chaque siècle ?
c. Les années multiples de 4 sont‑elles toutes bissextiles ? Comment justifier ce choix ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Obtenir et interpréter un développement en fractions continues afin de déterminer plusieurs approximations d'un même nombre à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Python
On donne l'algorithme en Python ci-dessous correspondant au calendrier choisi par les Perses.

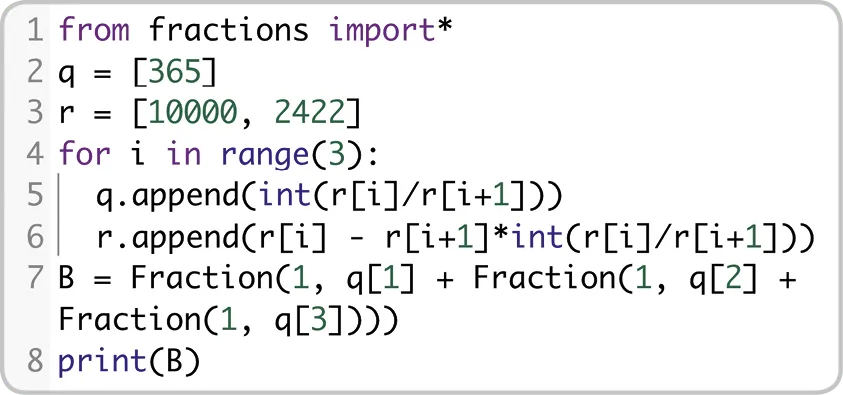
1. Quelle est la nature des variables q et r créées en début de programme ? Pourquoi a‑t‑on choisi ce type de variables plutôt que des variables numériques ?
2. Que représentent les nombres int(r[i]/r[i+1]) et r[i]-r[i+1]*int(r[i]/r[i+1]) ?
3. Interpréter le résultat affiché après exécution : combien de jours les Perses ajoutaient‑ils sur combien d'années ?
4. Modifier ce programme afin qu'il affiche l'erreur commise et le nombre d'années au bout desquelles l'erreur atteint un jour entier (appelé « validité »).


1. Quelle est la nature des variables q et r créées en début de programme ? Pourquoi a‑t‑on choisi ce type de variables plutôt que des variables numériques ?
2. Que représentent les nombres int(r[i]/r[i+1]) et r[i]-r[i+1]*int(r[i]/r[i+1]) ?
3. Interpréter le résultat affiché après exécution : combien de jours les Perses ajoutaient‑ils sur combien d'années ?
4. Modifier ce programme afin qu'il affiche l'erreur commise et le nombre d'années au bout desquelles l'erreur atteint un jour entier (appelé « validité »).
from fractions import* q = [365]r = [10000, 2422] for i in range(3): q.append(int(r[i]/r[i+1])) r.append(r[i]-r[i+1]*int(r[i]/r[i+1])) B = Fraction(1, q[1] + Fraction(1, q[2] + Fraction(1, q[3]))) print(B)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
1. Charger la feuille de calcul . Quelles formules doit-on entrer en A3 et en B4 afin de déterminer les dix premiers termes des suites (q_n) et (r_n) ?
2. Afin de calculer les valeurs approchées de \text{A} sans entrer à la main les formules de chaque fraction continue, on a entré dans les colonnes C et D les formules qui calculent le numérateur et le dénominateur des fractions \text{A}_0 ; \text{A}_1 ; \text{A}_2 ; …
Expliquer pourquoi la formule =C2-365*D2 entrée en F2 permet de remplir la colonne F puis interpréter les résultats de la ligne 5 correspondant à l'approximation choisie par les Perses.
3. On appelle validité le nombre d'années au bout desquelles l'erreur atteint un jour entier. Remplir les colonnes G et H en arrondissant les résultats de la colonne H à l'entier. Interpréter les résultats affichés ligne 11.
2. Afin de calculer les valeurs approchées de \text{A} sans entrer à la main les formules de chaque fraction continue, on a entré dans les colonnes C et D les formules qui calculent le numérateur et le dénominateur des fractions \text{A}_0 ; \text{A}_1 ; \text{A}_2 ; …
Expliquer pourquoi la formule =C2-365*D2 entrée en F2 permet de remplir la colonne F puis interpréter les résultats de la ligne 5 correspondant à l'approximation choisie par les Perses.
3. On appelle validité le nombre d'années au bout desquelles l'erreur atteint un jour entier. Remplir les colonnes G et H en arrondissant les résultats de la colonne H à l'entier. Interpréter les résultats affichés ligne 11.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Écrire la fraction continue \text{A}_3 donnée par les valeurs q_0 à q_4.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
