Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 8
Activités
Équations de droites
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AVecteur directeur d'une droite
Découvrir la notion de vecteur directeur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
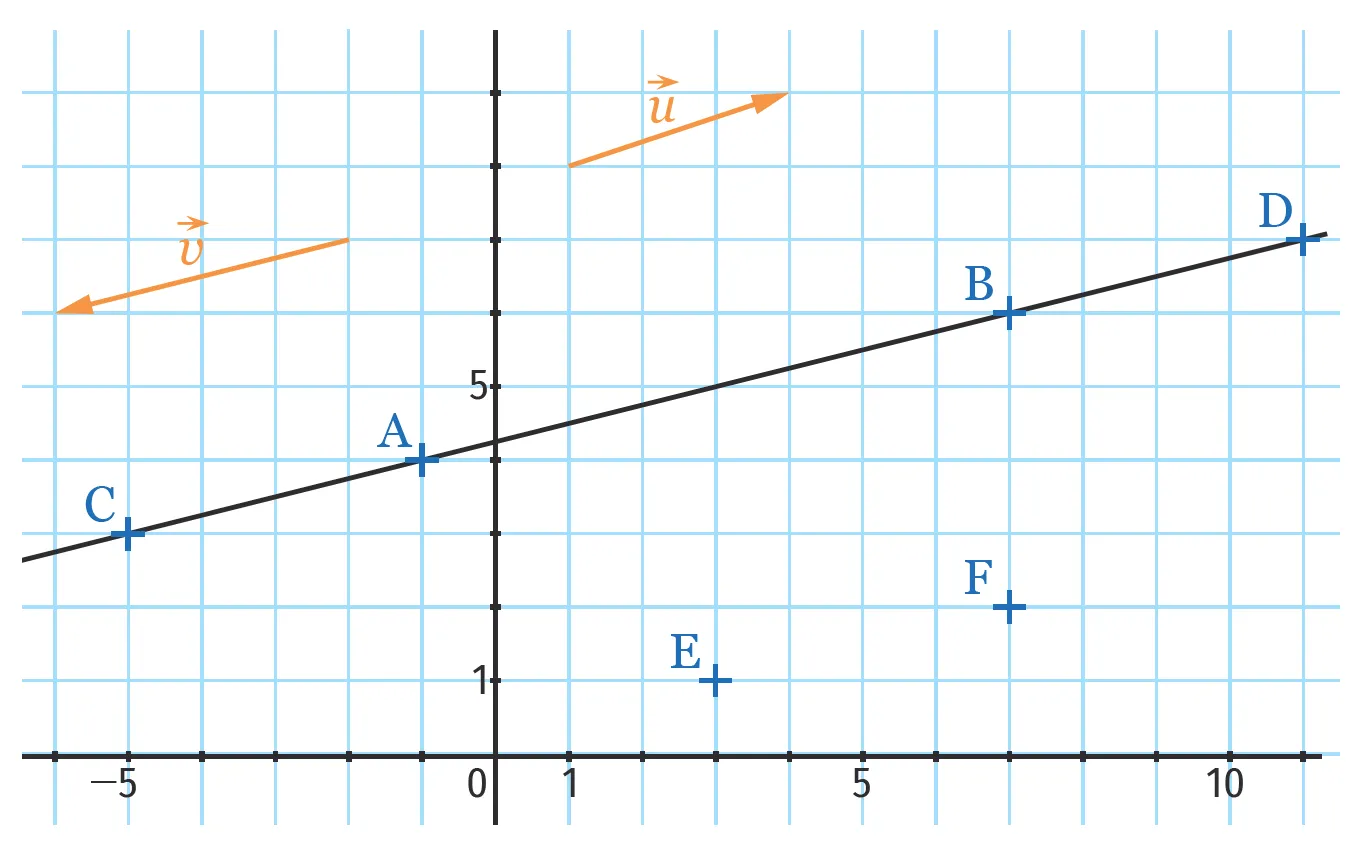
On se place dans un repère orthonormé.
On considère une droite d. \text{A}, \text{B}, \text{C} et \text{D} sont quatre points de cette droite et \text{E} et \text{F} sont deux points qui n'appartiennent pas à d.
On considère une droite d. \text{A}, \text{B}, \text{C} et \text{D} sont quatre points de cette droite et \text{E} et \text{F} sont deux points qui n'appartiennent pas à d.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
a) Calculer les coordonnées des vecteurs \overrightarrow{\text{AB}}, \overrightarrow{\text{AC}} et \overrightarrow{\text{EF}}.
b) Calculer les déterminants de ces vecteurs pris deux par deux. Que constate-t-on ?
Aide
Le déterminant de deux vecteurs (x\,;y) et (x'\,;y') est égal à xy' - x'y .
c) Ces vecteurs sont appelés vecteurs directeurs de d. Proposer deux autres vecteurs directeurs de d.
d) Déterminer par le calcul quel vecteur de \vec{u} et \vec{v} est un vecteur directeur de d.
2
a) Calculer la valeur du réel m tel que le vecteur \vec{w} de coordonnées (1 \:; m) soit un vecteur directeur de d.
b) Quelles sont les coordonnées du point d'intersection de la droite d avec l'axe des ordonnées ? Justifier.
3
On considère sur la droite d un point \text{M} quelconque de coordonnées (x\: ; y).
a) Calculer le déterminant des vecteurs \overrightarrow{\text{AM}} et \overrightarrow{\text{AB}} en fonction de x et y. Pourquoi ce déterminant est-il nul ?
b) En déduire que le point \text{M} vérifie la relation x - 4y + 17 = 0. Cette relation est appelée équation cartésienne de d.
c) En prenant le déterminant des vecteurs \overrightarrow{\text{BM}} et \overrightarrow{\text{AC}}, établir une seconde équation cartésienne de d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BilanQu'est-ce qu'un vecteur directeur d'une droite et une équation cartésienne de droite ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BVecteur directeur et équation de droite
Démontrer une propriété.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Soient a, b et c trois nombres réels. On veut démontrer la proposition suivante : « Si une droite d a pour équation ax + by + c = 0, alors le vecteur (-b\: ; a) est un vecteur directeur de d. »
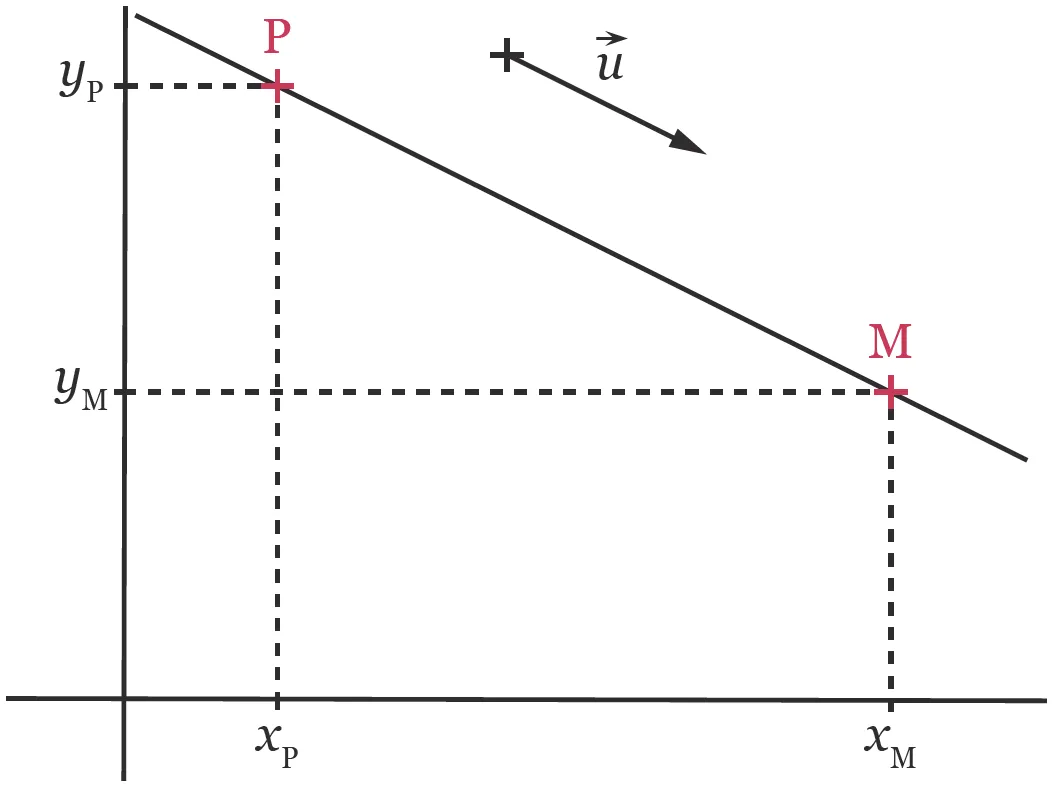
Dans un repère orthonormé, on considère donc une droite d d'équation ax + by + c = 0, deux points \text{P}(x_{\text{P}}\:; y_{\text{P}}) et \text{M}(x_{\text{M}} \:; y_{\text{M}}) appartenant à d et le vecteur \vec{u} de coordonnées (-b\: ; a).
Dans un repère orthonormé, on considère donc une droite d d'équation ax + by + c = 0, deux points \text{P}(x_{\text{P}}\:; y_{\text{P}}) et \text{M}(x_{\text{M}} \:; y_{\text{M}}) appartenant à d et le vecteur \vec{u} de coordonnées (-b\: ; a).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Pourquoi peut-on affirmer que ax_{\text{M}} + by_{\text{M}} + c = 0 ?
Aide
Si un point appartient à une droite, ses coordonnées vérifient l'équation de la droite.
2
Quelle relation peut-on établir entre les coordonnées du point \text{P} ?
3
En déduire la relation a(x_{\text{M}} - x_{\text{P}}) + b(y_{\text{M}} - y_{\text{P}}) = 0.
4
Traduire cette relation en termes de déterminant de deux vecteurs et conclure.
Logique
Il s'agirait pour être complet de démontrer qu'à tout vecteur (-b \:; a) on peut associer une équation de droite du type ax + by + c = 0.Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BilanQuel lien peut-on faire entre équation de droite et vecteur directeur ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CDroites sécantes
Déterminer l'intersection de deux droites.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un restaurateur réorganise sa salle. Il souhaite proposer à ses clients des tables pour deux personnes et des tables familiales pour six personnes.
Son fournisseur lui vend les tables « Duo » à 40 € et les tables « Famille » à 60 €.
Son objectif est d'atteindre exactement 60 couverts par repas. Pour cela, il dispose d'une subvention exceptionnelle de 900 € qu'il doit dépenser intégralement pour acheter les tables.
On appelle x le nombre de tables « Duo » et y le nombre de tables « Famille » à acheter.
Son fournisseur lui vend les tables « Duo » à 40 € et les tables « Famille » à 60 €.
Son objectif est d'atteindre exactement 60 couverts par repas. Pour cela, il dispose d'une subvention exceptionnelle de 900 € qu'il doit dépenser intégralement pour acheter les tables.
On appelle x le nombre de tables « Duo » et y le nombre de tables « Famille » à acheter.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Les contraintes du restaurateur sont-elles respectées lorsqu'il achète :a) 6 tables « Duo » et 8 tables « Famille » ?
b) 12 tables « Duo » et 7 tables « Famille » ?
2
a) Montrer que x et y doivent vérifier simultanément les deux équations suivantes : 2x + 6y = 60 et 2x + 3y = 45.
b) Dans un repère orthogonal, on a représenté les équations ci-dessus par les droites d et d'. Proposer une répartition des tables répondant au projet du restaurateur.
3
On souhaite résoudre le système d'inconnue (x\:;y) suivant :
\begin{cases}
2x + 6y=60 \\
2x + 3y=45
\end{cases}
a) Justifier que tout couple (x \:; y) vérifiant les deux équations de ce système vérifie aussi l'égalité 2x + 6y - (2x + 3y) = 15.
b) En déduire la valeur de y puis celle de x.
c) Conclure.
4
Lien avec le déterminant :
a) Déterminer deux vecteurs \vec{u} et \vec{u'}, vecteurs directeurs respectifs de d et d'.
b) Calculer leur déterminant. Pourquoi ne peut-il pas être nul ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan Comment déterminer par le calcul l'existence et les coordonnées de l'intersection de deux droites ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah