Mathématiques 2de
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Chapitre 8
Auto-évaluation
Exercices d'auto-évaluation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM réponse unique
QCM
réponse unique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
Soit d la droite d'équation cartésienne x + 5y - 7 = 0 . Un vecteur directeur de d a pour coordonnées :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Soit d la droite d'équation réduite y = - 3 x + \dfrac { 1 } { 2 }. Son coefficient directeur est égal à :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
Soient \mathrm { A } ( - 3\: ; - 1 ) et \mathrm {B} ( - 1\: ; 2 ). Alors une équation cartésienne de la droite (\mathrm { AB }) est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
Les droites d et d' d'équations 3x + 2y - 10 = 0 et y = -1\text{,}5x - 5\text{,}5 sont :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM réponses multiples
QCM
réponses multiples
[Une ou plusieurs bonnes réponses par question]
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
La droite d'équation 5x - 2y + 9 = 0 passe par les points :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
On donne \text{A} ( - 6 \:; 2 ) et \text{B} ( - 1\: ; 0 ). La droite ( \mathrm { AB } ) admet pour équation :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
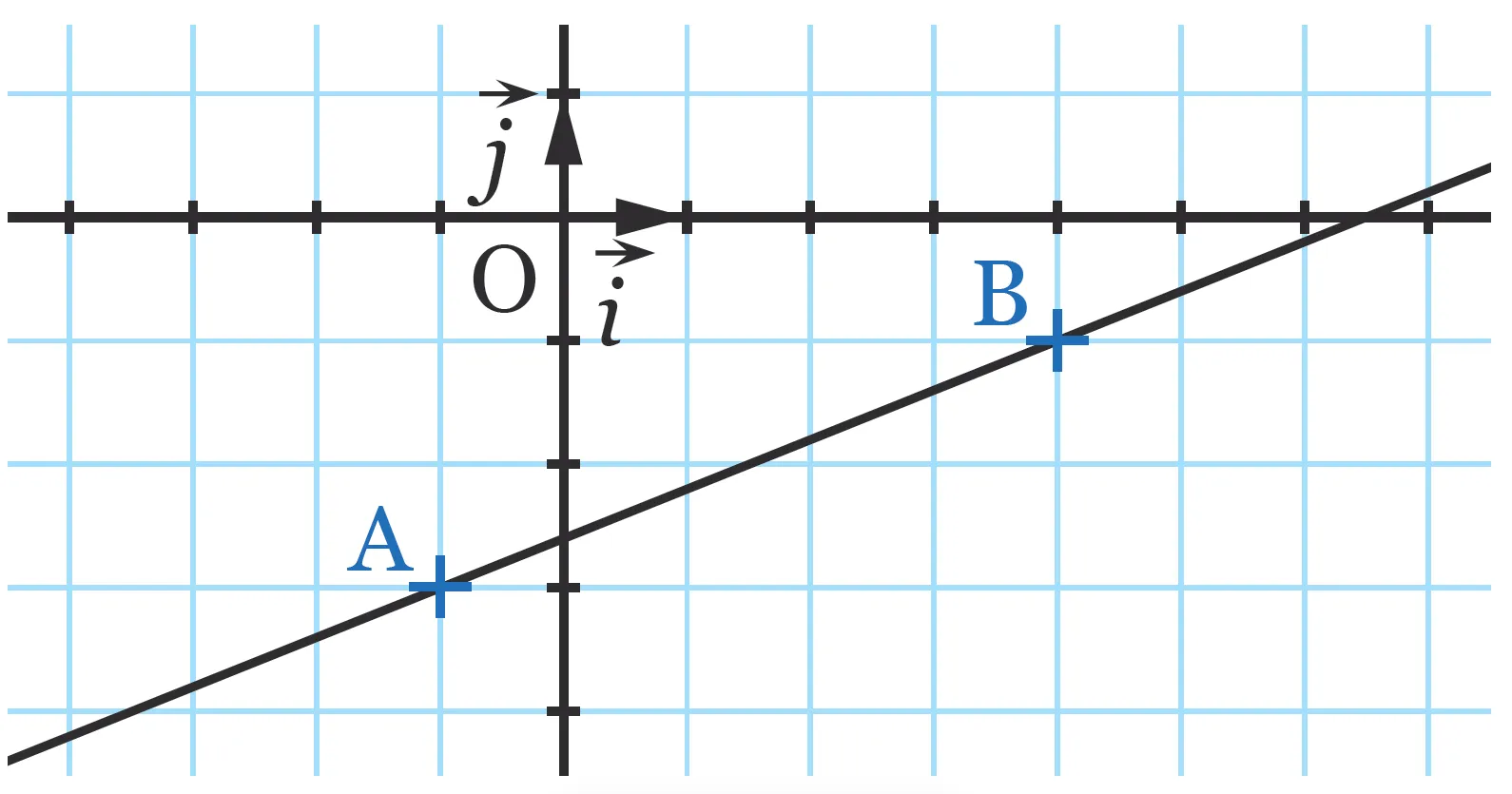
12
La droite (\text{AB}) a pour équation :

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
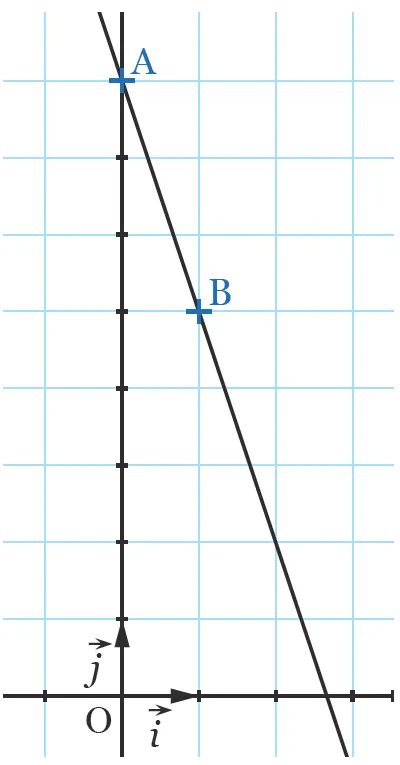
14
La droite (\text{AB}) admet pour vecteurs directeurs :

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
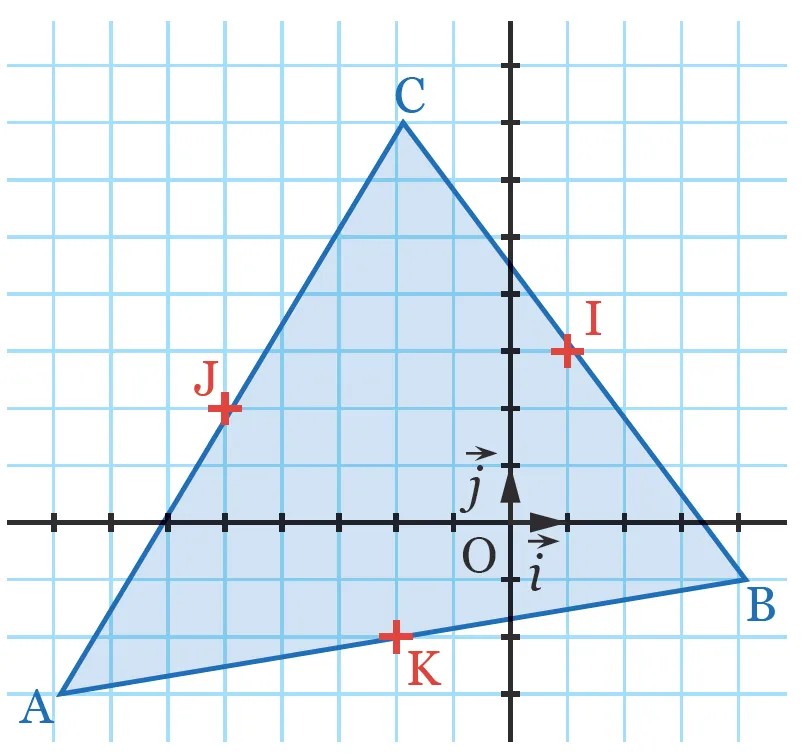
15
Dans un repère orthonormé, on considère les points \mathrm { A } ( - 8\: ; - 3 ) , \mathrm { B } ( 4\: ; - 1 ) et \mathrm { C } ( -2 \:; 7 ), ainsi que les milieux des côtés du triangle \mathrm { ABC } : \mathrm { I } ( 1\: ; 3 ) , \mathrm { J } ( - 5\: ; 2 ) et \mathrm { K } ( - 2 \:; - 2 ). On admet que les droites ( \mathrm { AI } ) , ( \mathrm { BJ } ) et ( \mathrm { CK } ) sont concourantes en un point. On cherche à calculer les coordonnées de ce point d'intersection.
1. Déterminer une équation de chacune des droites ( \mathrm { AI } ) et ( \mathrm { BJ } ).
2. Calculer les coordonnées de leur point d'intersection \mathrm { G }.
3. Vérifier que \mathrm { G } appartient à (\mathrm { CK }).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
