Chapitre 8
Entrainement 3
Positions relatives de droites
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Calculer.]
Dans chaque cas, déterminer une équation cartésienne de la droite d' parallèle à la droite d et passant par le point \mathrm { A } :
1. d : 2 x + y + 3 = 0 et \mathrm { A } ( - 1 \:; 5 )
2. d : x + y = 0 et \mathrm { A } ( 7 \:; 1 )
2. d : x + y = 0 et \mathrm { A } ( 7 \:; 1 )
3. d : x = 4 et \mathrm { A } ( 3\: ; 0 )
4. d : y = \dfrac { 1 } { 2 } x - \dfrac { 1 } { 4 } et \mathrm { A } ( - 3\: ; 2 )
4. d : y = \dfrac { 1 } { 2 } x - \dfrac { 1 } { 4 } et \mathrm { A } ( - 3\: ; 2 )
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
Algo
[Représenter.]
On considère une droite d d'équation y = mx + p et un point \text{A} de coordonnées (x_\text{A} \: ; y_\text{A}).
Écrire un algorithme qui donne l'équation de la droite d' parallèle à d et passant par \text{A}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
[Calculer.]
Démontrer que les points \text{A}, \text{B} et \text{C} sont alignés :
\text{A}(100\:;1\, 500), \text{B}(180\:;1\, 900) et \text{C}(198\:;1\, 990).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
[Calculer.]
Démontrer que les points \text{A}, \text{B} et \text{C} sont alignés :
\text{A}(0\:;- 4 \sqrt { 3 } + 1), \text{B}(3 \sqrt { 3 }\: ; 10 - 4 \sqrt { 3 }) et \text{C}(- 1 \:; 1 - 5 \sqrt { 3 }).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
[Raisonner.] Dans chacun des cas suivants, déterminer en justifiant si les points \text{A}, \text{B} et \text{C} sont alignés :
1. \mathrm { A } ( - 4 \:; - 4 ), \mathrm { B } ( 0 \:; 0 ) et \mathrm { C } ( 4\: ; 4 )
2. \mathrm { A } ( - 2 \:; 3 ), \mathrm { B } ( 1\:; 0 ) et \mathrm { C } ( 4 \:; 1 )
2. \mathrm { A } ( - 2 \:; 3 ), \mathrm { B } ( 1\:; 0 ) et \mathrm { C } ( 4 \:; 1 )
3. \mathrm { A } ( 5 \:; 2 ), \mathrm { B } ( 0 \:; 2 ) et \mathrm { C } ( 1 \:; 2 )
4. \mathrm { A } ( 4 \:; - 2 ), \mathrm { B } ( 4\: ; 3 ) et \mathrm { C } ( 0 \:; 3 )
4. \mathrm { A } ( 4 \:; - 2 ), \mathrm { B } ( 4\: ; 3 ) et \mathrm { C } ( 0 \:; 3 )
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
[Chercher.]
Sans calculer de longueur, démontrer que le quadrilatère \mathrm {ABCD} est un parallélogramme.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
[Chercher.]
Voici une capture d'écran du logiciel GeoGebra.

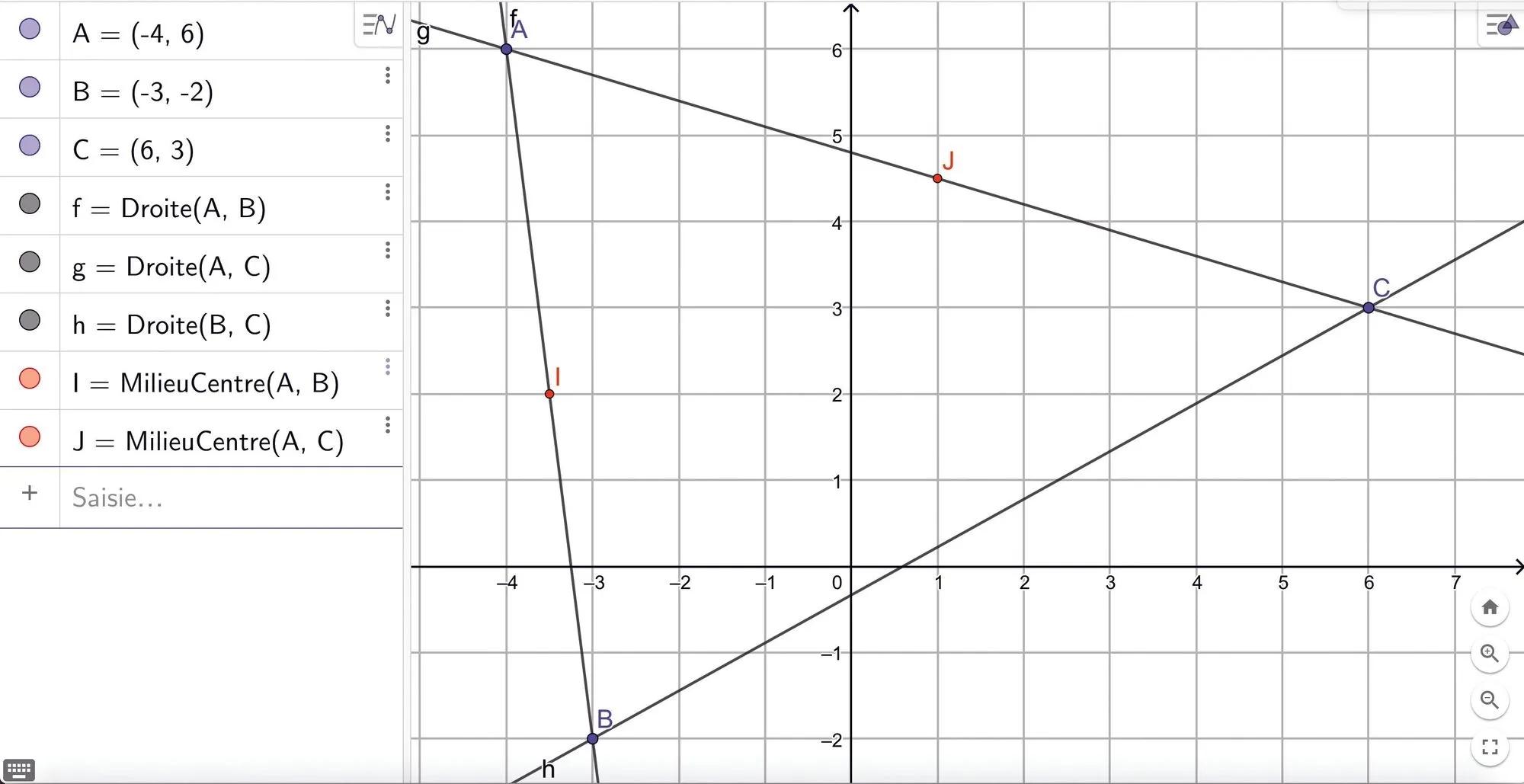
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
[Représenter.]
\text{ABCD} est un carré dont le côté mesure 4 cm. \text{DFC} et \text{BCH} sont des triangles équilatéraux.


Aide
On pourra se placer dans un repère convenablement choisi.
1. Calculer la hauteur de chaque triangle équilatéral.
2. Démontrer que les points \text{A}, \text{H} et \text{F} sont alignés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
[Représenter.]
\text{ABCD} est un carré dont le côté mesure 4 cm. \text{ABF} et \text{BDE} sont des triangles équilatéraux.
Quelle est la nature du quadrilatère \text{ACEF} ? Justifier.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
[Calculer.]
Dans un repère orthonormé, on considère les points \mathrm { A } ( 2 \:; 8 ) , \mathrm { B } ( 2 \: ; - 2 ) , \mathrm { C } ( 8\: ; 4 ) et \mathrm { D } ( 2\: ; 2 ).
1. Faire une figure.
2. Déterminer les coordonnées exactes du point \text{E} tel que :
- \text{E} appartient à la droite (\text{DC}) ;
- \text{E} n'appartient pas au segment [\text{DC}] ;
- \dfrac{\text{DE}}{\text{DC}} = \dfrac{2}{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
Python
[Représenter.]
On considère deux droites d _ { 1 } et d _ { 2 } d'équations a _ { 1 } x + b _ { 1 } y + c _ { 1 } = 0 et a _ { 2 } x + b _ { 2 } y + c _ { 2 } = 0 et le programme Python suivant :
def determinant(a1,b1,a2,b2): return(a1*b2 - a2*b1)
1. On souhaite compléter le programme pour savoir si les droites d_1 et d_2 sont parallèles. Quel test doit-on effectuer pour le savoir ?
2. On souhaite compléter le programme pour savoir ensuite si les droites d_1 et d_2 sont strictement parallèles ou confondues. Quel test doit-on effectuer ?
2. On souhaite compléter le programme pour savoir ensuite si les droites d_1 et d_2 sont strictement parallèles ou confondues. Quel test doit-on effectuer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
[Raisonner.]
Dans chaque cas, déterminer si le point \mathrm { A } ( 11\: ; 17 ) appartient à la droite d_1, à la droite d_2 ou aux deux. 1. d _ { 1 } : y = - 3 x + 50 et d _ { 2 } : y = 2\text{,}75 x - 13\text{,}75
2. d _ { 1 } : y = - x + 28 et d _ { 2 } : y = - 2 x + 41
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
[Raisonner.]
Les droites d'équations y = \pi x + 1 et y = \dfrac { 22 } { 7 } x - 1 sont-elles sécantes ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78
À l'aide d'un système, justifier que les droites d'équations x - y + 3 = 0 et 3x + 4y - 19 = 0 sont sécantes et déterminer leur intersection.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79
[Représenter.]
Déterminer à l'aide d'un argument graphique si les systèmes suivants possèdent zéro, une ou une infinité de solutions :
1. \begin{cases} { 3 x + y = 4 } \\ { 3 x - y = 1 } \end{cases}
2. \begin{cases} { - x + 2 y = 0 } \\ { - 0\text{,}5 x + y = 1 } \end{cases}
2. \begin{cases} { - x + 2 y = 0 } \\ { - 0\text{,}5 x + y = 1 } \end{cases}
3. \begin{cases} { 4 x + 7 y = - 2 } \\ { - 2 x - 3\text{,}5 y = 1 } \end{cases}
4. \begin{cases} { - 2 x + 3 y = 5 } \\ { 3 x - 2 y = 5 } \end{cases}
4. \begin{cases} { - 2 x + 3 y = 5 } \\ { 3 x - 2 y = 5 } \end{cases}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
80
[Chercher.]
En détaillant la démarche, proposer deux équations de droites qui se coupent au point de coordonnées (3\: ; 1).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
81
[Chercher.]
Dans un repère, les droites d'équations d _ { 1 } : 2 x - y - 5 = 0, d _ { 2 } : x + 4 y - 25 = 0 et d _ { 3 } : x - 5 y + 11 = 0 se coupent en formant un triangle \text{ABC}.


1. Associer aux coordonnées de chaque sommet le couple solution de chacun des systèmes suivants :
\mathrm { S } _ { 1 } : \begin{cases} { x + 4 y = 25 } \\ { - 2 x + y = - 5 } \end{cases}
\mathrm { S } _ { 2 } : \begin{cases} { - 2 x + y = - 5 } \\ { x - 5 y = - 11 } \end{cases}
\mathrm { S } _ { 3 } : \begin{cases} { x - 5 y = - 11 } \\ { x + 4 y = 25 } \end{cases}
2. Vérifier les résultats par le calcul.
\mathrm { S } _ { 1 } : \begin{cases} { x + 4 y = 25 } \\ { - 2 x + y = - 5 } \end{cases}
\mathrm { S } _ { 2 } : \begin{cases} { - 2 x + y = - 5 } \\ { x - 5 y = - 11 } \end{cases}
\mathrm { S } _ { 3 } : \begin{cases} { x - 5 y = - 11 } \\ { x + 4 y = 25 } \end{cases}
2. Vérifier les résultats par le calcul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82
[Représenter.]
Par lecture graphique, proposez le couple solution à chaque système. Vérifier par le calcul.


1. \begin{cases} { x - y = - 1 } \\ { - x + 7 y = - 17 } \end{cases}
2. \begin{cases} { -5x - y = - 13 } \\ { x - y = - 1 } \end{cases}
3. \begin{cases} { -x + 7y = - 17 } \\ { - 5x - y = - 13 } \end{cases}
2. \begin{cases} { -5x - y = - 13 } \\ { x - y = - 1 } \end{cases}
3. \begin{cases} { -x + 7y = - 17 } \\ { - 5x - y = - 13 } \end{cases}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83
[Représenter.]
Résoudre les systèmes suivants graphiquement.
1. \begin{cases} { 5x - y = 8 } \\ { - 3x + 2 y =12 } \end{cases}
2. \begin{cases} { 2x + y = - 10 } \\ { -1\text{,}5x + 2 y = 13 } \end{cases}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84
[Calculer.] On a réalisé cette capture d'écran du logiciel GeoGebra. Déterminer par le calcul les coordonnées des points \text{A}, \text{B} et \text{C}.

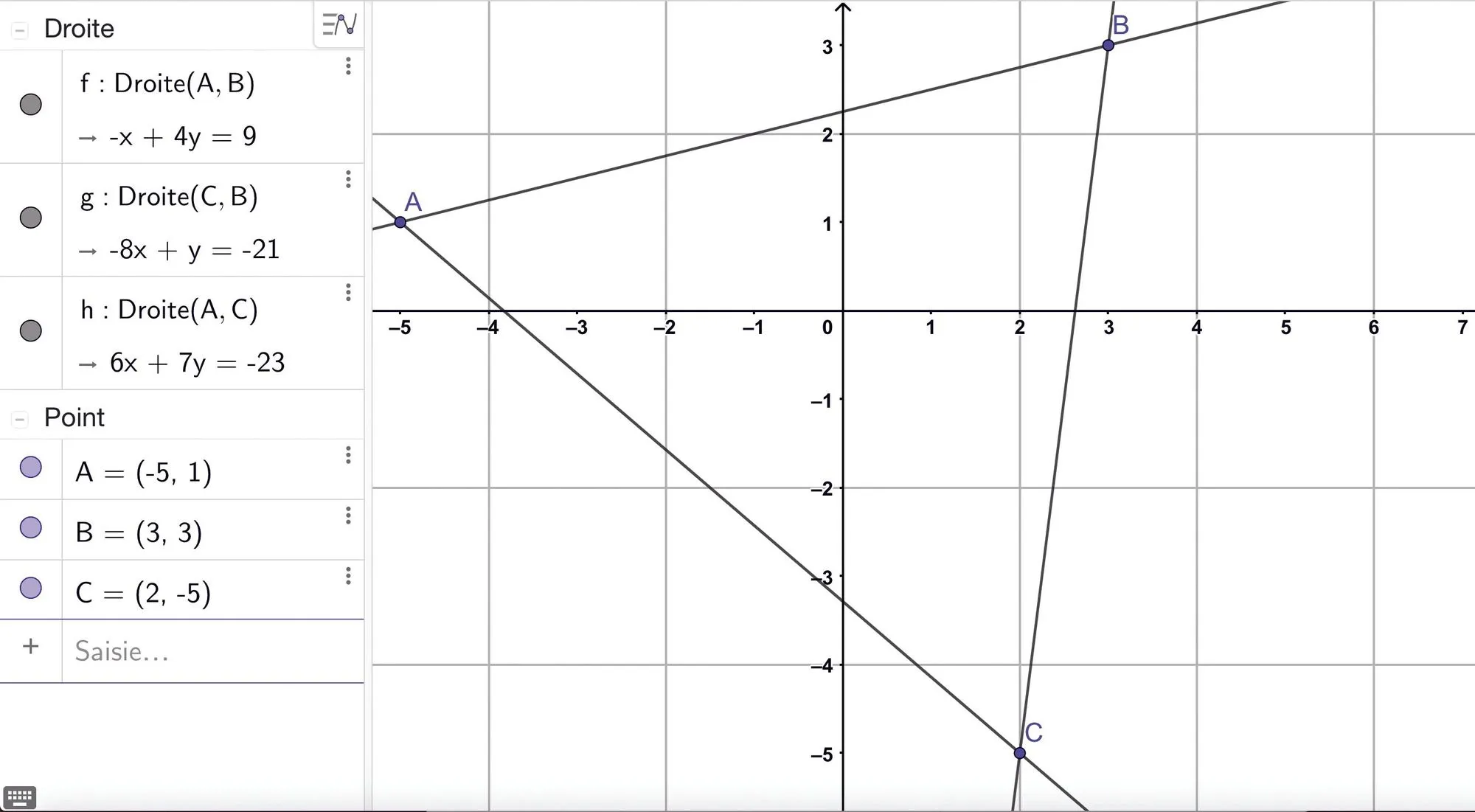
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85
Tableur
[Raisonner.]
On a réalisé cette feuille de calcul qui donne l'ordonnée des points de deux droites pour différentes valeurs de x.

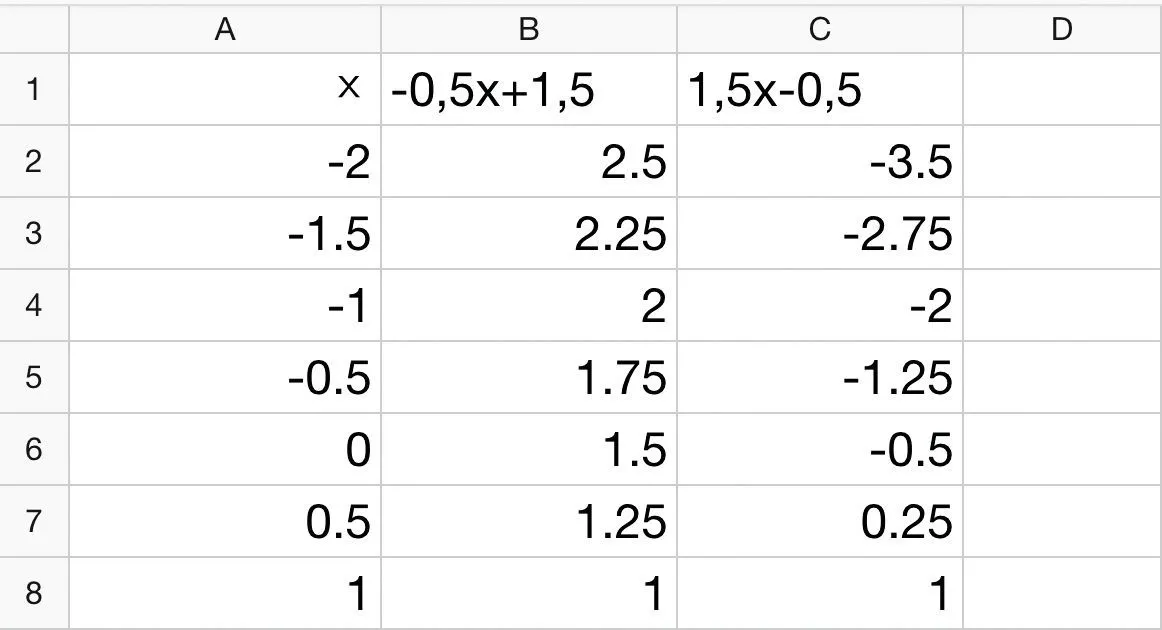


1. Que doit-on entrer comme formule dans les cellules B2 et C2 puis étirer vers le bas ?
2. Les droites d'équations y = -0\text{,}5x + 1\text{,}5 et y = 1\text{,}5x - 0\text{,}5 sont-elles sécantes ? Si oui, quelles sont les coordonnées de leur point d'intersection ?
2. Les droites d'équations y = -0\text{,}5x + 1\text{,}5 et y = 1\text{,}5x - 0\text{,}5 sont-elles sécantes ? Si oui, quelles sont les coordonnées de leur point d'intersection ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
86
[Communiquer.]
On a réalisé la figure ci-dessous sous GeoGebra.

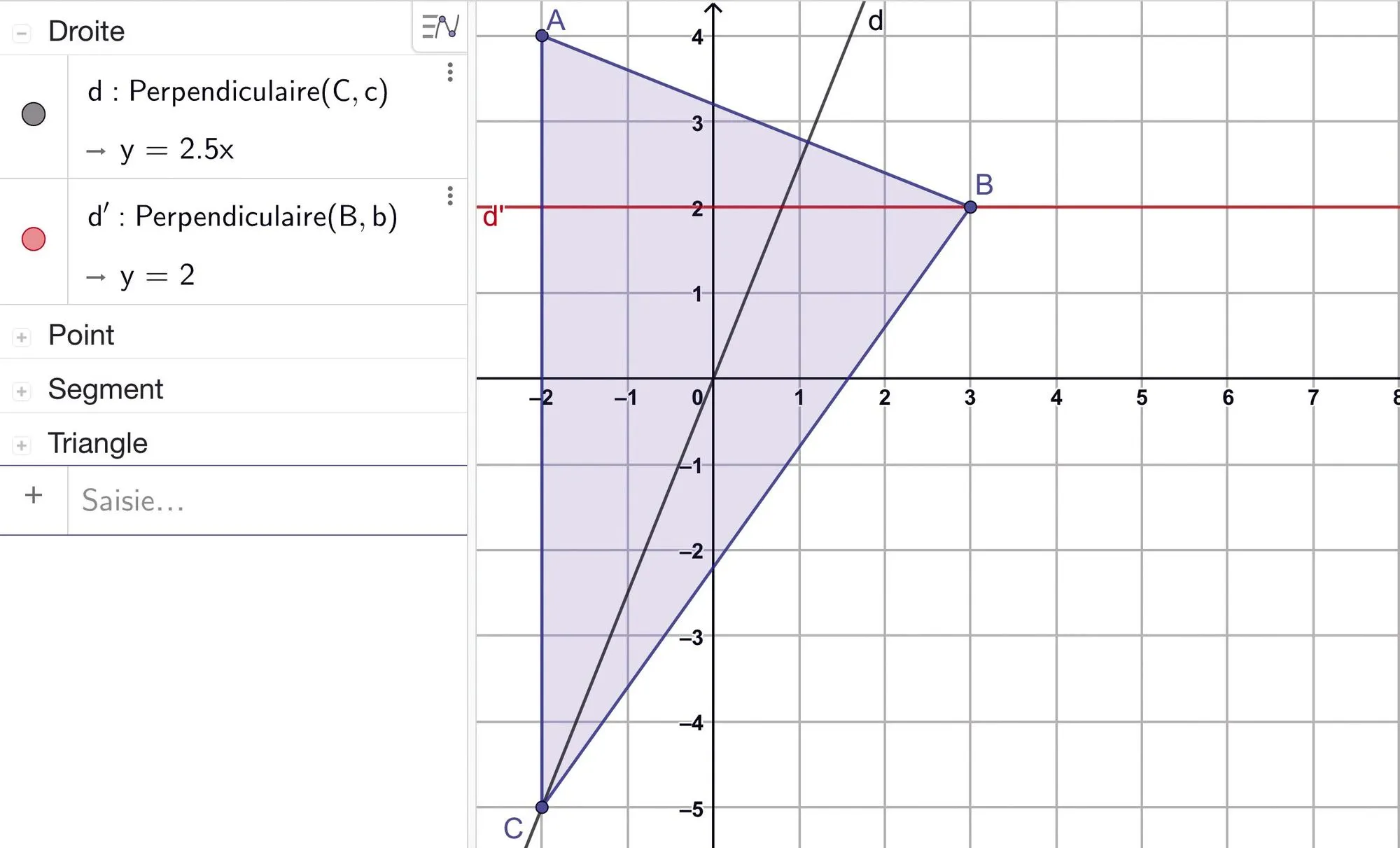


1. Que représentent les droites d et d' pour le triangle \text{ABC} ?
2. On a réalisé la feuille de calcul ci-dessous.


Expliquer comment lire les coordonnées de l'orthocentre du triangle \text{ABC}.
2. On a réalisé la feuille de calcul ci-dessous.


Expliquer comment lire les coordonnées de l'orthocentre du triangle \text{ABC}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
87
Python
[Calculer.]
Voici un programme réalisé avec Python :
def resolution(a, b, c, d, e, f): det = a*e-d*b if det == 0: return(True) else: return(False)
1. Quel est le rôle de la variable « det » ?
2. À quoi sert ce programme ?
3. Exécuter ce programme avec les valeurs suivantes :
a = 3 , b = 6 , c = -1 , d = 2 , e = 4 , et f = -7 .
4. Que peut-on déduire de ce résultat ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
88
Algo
[Effectuer.]On considère deux droites sécantes d et d' d'équations ax + by + c = 0 et a'x + b'y + c' = 0 .
1. Exprimer en fonction de a, b , c , a', b' et c' les coordonnées de leur point d'intersection.
2. Modifier le programme de l'exercice précédent pour qu'il affiche les coordonnées de l'intersection des deux droites lorsqu'elles sont sécantes.
def resolution(a, b, c, d, e, f): det = a*e-d*b if det == 0: return(True) else: return(False)
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

