Chapitre 8
Applications directes
Exercices d'applications directes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'oral
Envie de réaliser ces exercices à l'oral ? Enregistrez-vous !
Enregistreur audio
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
Dans chaque cas, déterminer deux vecteurs directeurs de la droite d dont une équation est donnée ci-dessous. 1. 3 x - 4 y + 1 = 0
2. y = 2
3. x = 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Dans chaque cas, déterminer le coefficient directeur de la droite d dont une équation est donnée ci-dessous. 1. - 4 x + 2 y + 1 = 0
2. x - 3 y = 0
3. 5 x - 5 y - 5 = 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Dans chaque cas, déterminer le coefficient directeur de la droite \text{(AB)} . 1. \mathrm { A } ( 1\: ; 1 ) et \mathrm { B } ( - 5 \:; 0 )
2. \mathrm {A} ( - 0\text{,}5\: ; 3 ) et \mathrm {B} ( 0\text{,}5\: ; - 2 )
3. \mathrm {A} \left( - \dfrac { 2 } { 3 } \:; \dfrac { 1 } { 4 } \right) et \mathrm { B } \left( \dfrac { 1 } { 3 }\: ; 1\text{,}25 \right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
Donner deux vecteurs directeurs de chacune des droites tracées :
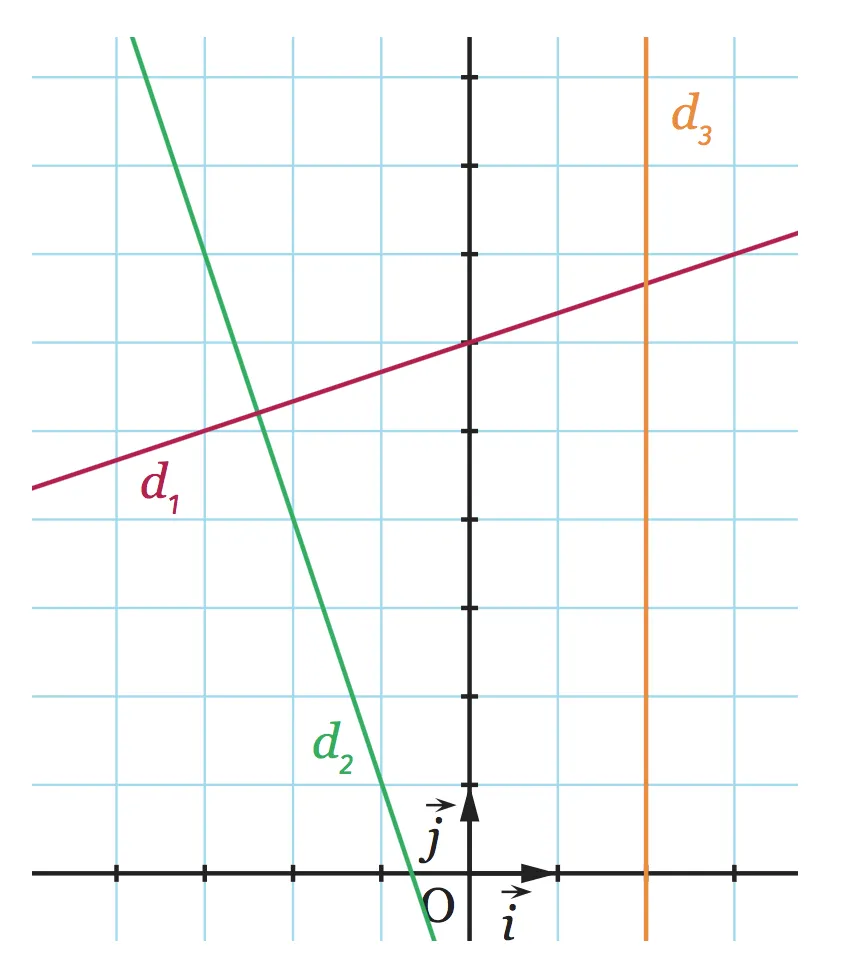
1. d_1
2. d_2
3. d_3
2. d_2
3. d_3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Donner un vecteur directeur de chaque droite dont une équation est donnée. 1. - 3 x + y - 2 = 0
2. \dfrac { 1 } { 2 } x - 4 y = 5
3. x = 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Dans chaque cas, déterminer si les droites d et d' sont strictement parallèles, sécantes ou confondues. 1. d : 3 x - 2 y + 7 = 0 et d ^ { \prime } : 3 x + 2 y - 7 = 0
2. d : \dfrac { 7 } { 3 } x - y + 2 = 0 et d ^ { \prime } : 7 x - 3 y + 9 = 0
3. d : x + 7 = 0 et d ^ { \prime } : - 5 x - 35 = 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Dans chaque cas, déterminer l'équation réduite de la droite dont on donne une équation cartésienne. 1. - 2 x + y + 1 = 0
2. - 1\text{,}5 x + 3 y - 4\text{,}5 = 0
3. - \dfrac { 7 } { 3 } y - 3 = 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Déterminer l'équation réduite de la droite passant par \text{A} et de coefficient directeur m. 1. \text{A} ( 5 \:; 2 ) et m = - 3
2. \mathrm { A } ( - 4 \:; - 1 ) et m = \dfrac { 1 } { 2 }
3. \mathrm { A } \left( - \dfrac { 1 } { 7 } \:; \dfrac { 3 } { 7 } \right) et m = 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Dans chaque cas, déterminer une équation de la droite \text{(AB)}. 1. \mathrm { A } ( - 6\: ; - 1 ) et \mathrm {B} ( 3 \:; 3 )
2. \mathrm {A} ( 5 \:; 0 ) et \mathrm {B} ( 5\: ; 2 )
3. \mathrm { A } \left( 4 \:; - \dfrac { 7 } { 9 } \right) et \mathrm { B } \left( 0 \:; \dfrac { 2 } { 9 } \right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Déterminer une équation de la droite passant par \text{A} et de vecteur directeur \vec{u}. 1. \mathrm { A } ( 0\: ; 4 ) et \vec { u } ( 4\: ; - 1 )
2. \mathrm {A} ( 5 \:; 2 ) et \vec { u } ( - 2 \:; 1 )
3. \mathrm { A } ( - 3\: ; 0 ) et \vec { u } ( 0 \:; 5 )
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Résoudre chacun des systèmes suivants par combinaisons linéaires et interpréter graphiquement le résultat. 1. \begin{cases} { - 3 x + 4 y = 5 } \\ { 3 x + 2 y = 7 } \end{cases}
2. \begin{cases} { - x + 5 y = 7 } \\ { 5 x + 10 y = 0 } \end{cases}
3. \begin{cases} { 5 x + 7 y = - 6 } \\ { - 3 x - 2 y = 8 } \end{cases}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Résoudre chacun des systèmes suivants par substitution et interpréter graphiquement le résultat. 1. \begin{cases} { - x + 2 y = - 1 } \\ { 3 x - 5 y = 7 } \end{cases}
2. \begin{cases} { 7 x - 0\text{,}5 y = 3 } \\ { - 4 x + 2 y = 12 } \end{cases}
3. \begin{cases} { 1\text{,}5 x + 4 y = - 1 } \\ { \dfrac { 1 } { 3 } x - 2 y = - 6 } \end{cases}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
Dans chaque cas, déterminer les coordonnées du point d'intersection des droites \text{(AB)} et \text{(CD)}. 1. \mathrm {A} ( - 5 \:; 7 ) , \mathrm {B} ( 2 \:; 0 ) , \mathrm{C} ( - 1 \:; 6 ) et \mathrm{D} ( 3\: ; 8 )
2. \mathrm {A} ( 0 \:; 3 ) , \mathrm {B} ( 2 \:; 4 ) , \mathrm {C} ( - 1 \:; 8 ) et \mathrm {D} ( - 1 \:; 5 )
3. \mathrm {A} ( 0 \:; 1 ) , \mathrm {B} ( - 2\: ; 9 ) , \mathrm {C} ( 2\: ; 8 ) et \mathrm {D} ( - 2 \:; 8 )
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Dans un repère orthonormé, tracer les droites suivantes. 1. d_1 d'équation cartésienne {- x + 2 y + 4 = 0 \mathrm{.}}
2. d_2 passant par \mathrm {A} ( - 4\: ; 2 ) et de vecteur directeur \vec { u } ( 4\: ; - 3 ) \mathrm{.}
3. d_3 d'équation réduite {y = - x + 4\text{,}5 \mathrm{.}}
4. d_2 passant par \mathrm { B } ( - 2\: ; 4 ) et de coefficient directeur -1\mathrm{,}5 \mathrm{.}
GeoGebra
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
