Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de soci été
Chapitre 4
Cours 2
Fonction inverse, fonction cube
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AFonction inverse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
- La fonction inverse est la fonction définie sur \mathbb { R } ^ { * } = ] - \infty\:; 0 [ \cup ] 0\:; + \infty [ qui, à tout réel x différent de 0, associe son inverse \dfrac { 1 } { x }.
- Sa courbe représentative est une hyperbole.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
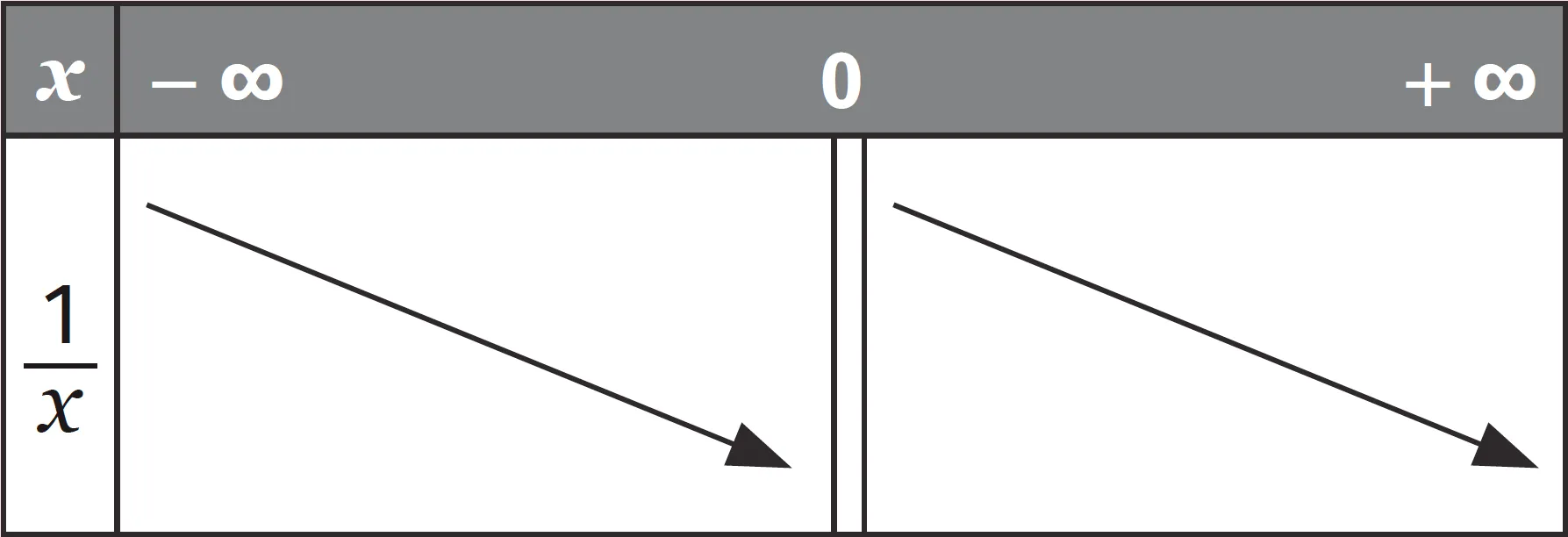
Propriété
La fonction inverse :
1. est impaire ;
2. ne s'annule pas sur son ensemble de définition ;
3. est strictement décroissante sur ] - \infty\:; 0 [ et strictement décroissante sur ] 0\:; + \infty [.
1. est impaire ;
2. ne s'annule pas sur son ensemble de définition ;
3. est strictement décroissante sur ] - \infty\:; 0 [ et strictement décroissante sur ] 0\:; + \infty [.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La fonction inverse n'est pas décroissante sur \mathbb { R } ^ { * }. En effet, on a par exemple - 2 \lt 3 mais \dfrac { 1 } { - 2 } \lt \dfrac { 1 } { 3 }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
1. Soit x \in \mathbb { R } ^ { * }. \dfrac { 1 } { - x } = - \dfrac { 1 } { x } donc l'image de -x est l'opposée de l'image de x .
2. Supposons qu'il existe un réel x tel que \dfrac { 1 } { x } = 0. Alors 1 = 0 \times x, d'où 0 = 1. C'est absurde. Donc la fonction inverse ne s'annule pas sur \mathbb { R } ^ { * }.
3. Voir exercice p. 135
2. Supposons qu'il existe un réel x tel que \dfrac { 1 } { x } = 0. Alors 1 = 0 \times x, d'où 0 = 1. C'est absurde. Donc la fonction inverse ne s'annule pas sur \mathbb { R } ^ { * }.
3. Voir exercice p. 135
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le point 2. utilise un raisonnement par l'absurde : si un postulat de départ induit une contradiction, alors ce postulat est faux.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
EXCLU. PREMIUM 2023
Genially
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
La fonction inverse est strictement décroissante sur ] - \infty\:; 0[ et
sur ] 0\:; + \infty [.
1. a. \dfrac { 1 } { 5 } \gt \dfrac { 1 } { 8 } car 5 \lt 8 b. - \dfrac { 1 } { 2 } \lt - \dfrac { 1 } { 3 } car -2 \gt -3
c. \dfrac { 3 } { 7 } \lt \dfrac { 3 } { 5 } car \dfrac { 7 } { 3 } \gt \dfrac { 5 } { 3 } d. \dfrac { 2 } { 5 } \gt - \dfrac { 4 } { 3 } car les signes sont opposés.
2. On a - 1 \lt - \dfrac { 1 } { 2 } \lt \dfrac { 1 } { 2 \pi } \lt \dfrac { 1 } { 3 } car -2 \lt -1 \lt 0 et 0 \lt 3 \lt 2 \pi.
1. a. \dfrac { 1 } { 5 } \gt \dfrac { 1 } { 8 } car 5 \lt 8 b. - \dfrac { 1 } { 2 } \lt - \dfrac { 1 } { 3 } car -2 \gt -3
c. \dfrac { 3 } { 7 } \lt \dfrac { 3 } { 5 } car \dfrac { 7 } { 3 } \gt \dfrac { 5 } { 3 } d. \dfrac { 2 } { 5 } \gt - \dfrac { 4 } { 3 } car les signes sont opposés.
2. On a - 1 \lt - \dfrac { 1 } { 2 } \lt \dfrac { 1 } { 2 \pi } \lt \dfrac { 1 } { 3 } car -2 \lt -1 \lt 0 et 0 \lt 3 \lt 2 \pi.
Pour s'entraîner
Exercices p. 131 ; et p. 134
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
1. Compléter sans calculatrice avec \lt ou \gt~:a. \dfrac { 1 } { 5 } \dots \dfrac { 1 } { 8 }
b. - \dfrac { 1 } { 2 } \ldots - \dfrac { 1 } { 3 }
c. \dfrac { 3 } { 7 } \dots \dfrac { 3 } { 5 }
d. \dfrac { 2 } { 5 } \dots - \dfrac { 4 } { 3 }
2. Ranger dans l'ordre croissant les nombres suivants : - \dfrac { 1 } { 2 }\:; \dfrac { 1 } { 2 \pi }\:; - 1\:; \dfrac { 1 } { 3 }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Si a et b sont des réels non nuls de même signe,
l'application de la fonction inverse change l'ordre.
Si a \lt b alors \dfrac { 1 } { a } \gt \dfrac { 1 } { b }.
Si a \lt 0 et b \gt 0 alors \dfrac { 1 } { a } \lt 0 et \dfrac { 1 } { b } > 0 donc on a toujours \dfrac { 1 } { a } \lt \dfrac { 1 } { b } .
2. On regroupe les négatifs, puis les positifs et on les classe grâce aux variations de la fonction inverse.
Si a \lt b alors \dfrac { 1 } { a } \gt \dfrac { 1 } { b }.
Si a \lt 0 et b \gt 0 alors \dfrac { 1 } { a } \lt 0 et \dfrac { 1 } { b } > 0 donc on a toujours \dfrac { 1 } { a } \lt \dfrac { 1 } { b } .
2. On regroupe les négatifs, puis les positifs et on les classe grâce aux variations de la fonction inverse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BFonction cube
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La fonction inverse et la fonction cube sont impaires : leur courbe représentative est symétrique par rapport à l'origine du repère.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
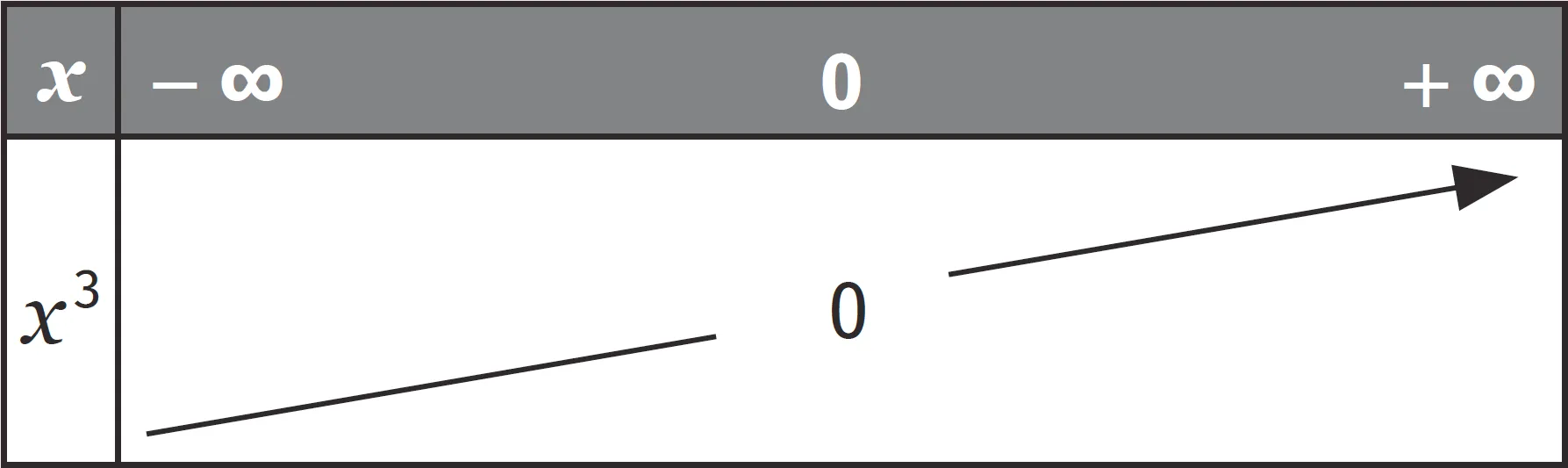
Propriété
La fonction cube :
1. est impaire ;
2. est strictement croissante sur \mathbb { R }.
1. est impaire ;
2. est strictement croissante sur \mathbb { R }.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
1. Pour tout x \in \mathbb { R }, ( - x ) ^ { 3 } = ( - x ) \times ( - x ) \times ( - x ) = - x \times x \times x = - x ^ { 3 } donc l'image de
-x est l'opposée de l'image de x : la fonction cube est impaire.
2. La démonstration de ce point est faite dans exercice p. 135
2. La démonstration de ce point est faite dans exercice p. 135
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété (admise)
Pour tout réel a, l'équation x ^ { 3 } = a admet exactement une solution, que l'on appelle racine cubique de a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La racine cubique d'un réel a est notée \sqrt [ 3 ] { a }. Par définition ( \sqrt [ 3 ] { a } ) ^ { 3 } = a.
On peut démontrer que, pour tous réels a et b, \sqrt [ 3 ] { a \times b } = \sqrt [ 3 ] { a } \times \sqrt [ 3 ] { b }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
1. 2 ^ { 3 } = 2 \times 2 \times 2 = 8\: ; \left( \dfrac { 1 } { 3 } \right) ^ { 3 } = \dfrac { 1 ^ { 3 } } { 3 ^ { 3 } } = \dfrac { 1 } { 27 }\: ; \sqrt { 5 } ^ { 3 } = \sqrt { 5 } ^ { 2 } \times \sqrt { 5 } = 5 \sqrt { 5 }.
2. L'équation x ^ { 3 } = 125 admet pour unique solution x = 5 donc \sqrt [ 3 ] { 125 } = 5.
2. L'équation x ^ { 3 } = 125 admet pour unique solution x = 5 donc \sqrt [ 3 ] { 125 } = 5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
1. Résoudre dans \mathbb { R } les équations suivantes :
a. x ^ { 3 } = 8 b. x ^ { 3 } = - 27 c. x ^ { 3 } = \dfrac { 8 } { 27 }
2. Ranger dans l'ordre croissant les nombres suivants : ( - 2 ) ^ { 3 }\: ; \pi ^ { 3 }\: ; \dfrac { 64 } { 125 }\: ; \left( - \dfrac { 3 } { 2 } \right) ^ { 3 }.
a. x ^ { 3 } = 8 b. x ^ { 3 } = - 27 c. x ^ { 3 } = \dfrac { 8 } { 27 }
2. Ranger dans l'ordre croissant les nombres suivants : ( - 2 ) ^ { 3 }\: ; \pi ^ { 3 }\: ; \dfrac { 64 } { 125 }\: ; \left( - \dfrac { 3 } { 2 } \right) ^ { 3 }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Il convient de connaître le cube des entiers 0, ... , 5 au moins. Par imparité de x \mapsto x ^ { 3 }, on connaît alors celui
de –5, ... , 0.
2. On utilise la stricte croissance de la fonction cube pour ordonner les réels en rangeant d'abord les antécédents dans l'ordre croissant. L'ordre ne change alors pas.
2. On utilise la stricte croissance de la fonction cube pour ordonner les réels en rangeant d'abord les antécédents dans l'ordre croissant. L'ordre ne change alors pas.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
1. a. x = 2
b. x = - 3
c. x ^ { 3 } = \left( \dfrac { 2 } { 3 } \right) ^ { 3 } donc x = \dfrac { 2 } { 3 }
2. On a : - 2 \lt - \dfrac { 3 } { 2 } \lt \dfrac { 4 } { 5 } \lt \pi donc, comme x \mapsto x ^ { 3 } est strictement croissante sur \mathbb { R }, on a : ( - 2 ) ^ { 3 } \lt \left( - \dfrac { 3 } { 2 } \right) ^ { 3 } \lt \dfrac { 64 } { 125 } \lt \pi ^ { 3 }.
2. On a : - 2 \lt - \dfrac { 3 } { 2 } \lt \dfrac { 4 } { 5 } \lt \pi donc, comme x \mapsto x ^ { 3 } est strictement croissante sur \mathbb { R }, on a : ( - 2 ) ^ { 3 } \lt \left( - \dfrac { 3 } { 2 } \right) ^ { 3 } \lt \dfrac { 64 } { 125 } \lt \pi ^ { 3 }.
Pour s'entraîner
Exercices p. 131, et p. 135
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah