Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Nombres et calculs
Fonctions
Ch. 1
Généralités sur les fonctions
Ch. 2
Variations de fonctions
Ch. 3
Fonctions affines
Ch. 4
Fonctions de référence
Géométrie
Ch. 5
Repérage et configuration dans le plan
Ch. 6
Notion de vecteur
Ch. 7
Colinéarité de vecteurs
Ch. 8
Équations de droites
Statistiques et probabilités
Ch. 9
Informations chiffrées
Ch. 10
Statistiques descriptives
Ch. 11
Probabilités et échantillonnage
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de collège
Jeux de société
Préparer la Première
Fonctions
17 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
f est définie sur \mathbb { R } par f(x) = 3x^2 - 5x + 2 . 1. Déterminer une expression simplifiée en fonction de x de :
a. f(x - 1)
b. f(x + 1)
c. f(x + 2)
2. Étudier le signe de f(x + 1) - f(x) en fonction de x .
2. Étudier le signe de f(x + 1) - f(x) en fonction de x .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Étudier la parité des fonctions définies sur \mathbb { R } par :
1. f ( x ) = - 5 x ^ { 2 } + 6
2. g ( x ) = 2 x ^ { 3 } - 5 x ^ { 2 }
3. h ( x ) = \dfrac { - 4 x } { x ^ { 2 } + 1 }
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
f et g sont définies sur \mathbb { N } par f(n) = 2^n et g ( n ) = \left( \dfrac { 1 } { 3 } \right) ^ { n }.
Déterminer une expression simplifiée, en fonction de n , de f(n + 1) - f(n) puis de g(n + 1) - g(n) .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Montrer que, pour tout réel x appartenant à \left[ \dfrac { 1 } { 2 }\: ; + \infty \right[, on a : x \geqslant \sqrt { 2 x - 1 } .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
On considère un réel x tel que - 3 \leqslant x \lt 4. Déterminer un encadrement de :
1. ( x + 3 ) ^ { 2 } + 2
2. 1 - 3 x ^ { 2 }
3. 7 x ^ { 3 } - 2
2. 1 - 3 x ^ { 2 }
3. 7 x ^ { 3 } - 2
4. \sqrt { x + 3 } - 2
5. 6 - 3 ( x - 1 ) ^ { 2 }
5. 6 - 3 ( x - 1 ) ^ { 2 }
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
1.
a. Résoudre dans \mathbb { R } l'équation 2x^2 - 18 = 0 .
b. En déduire les solutions de l'équation 2x^4 - 18 = 0 .
2. a. Factoriser 2x^2 - 18 pour x \in \mathbb { R }.
b. En déduire les solutions de l'équation 2x^4 - 18 = 0 .
2. a. Factoriser 2x^2 - 18 pour x \in \mathbb { R }.
b. En déduire le tableau de signes de la fonction définie
sur \mathbb { R } par f(x)=2x^2 - 18.
c. Résoudre dans \mathbb { R } l'inéquation 2x^4 - 18 \geqslant 0 .
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
c. Résoudre dans \mathbb { R } l'inéquation 2x^4 - 18 \geqslant 0 .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7
f est définie sur \mathbb { R } par f ( x ) = x ^ { 3 } - 2 x ^ { 2 } - 3 x + 4.
Le zoom est accessible dans la version Premium.
On note (\text{E}) l'équation f(x) = 0 . D'après ce graphique, on observe que l'équation (\text{E}) admet trois solutions : une solution entière et deux autres solutions notées \alpha et \beta.
1. Quelle est la solution entière de (\text{E}) ?
2. À l'aide de la calculatrice, déterminer un encadrement d'amplitude 10^{-2} des solutions \alpha et \beta.
3. a. Démontrer que, pour tout réel x , f ( x ) = ( x - 1 ) \left( x ^ { 2 } - x - 4 \right).
b. Démontrer que, pour tout réel x ,
x ^ { 2 } - x - 4 = \left( x - \dfrac { 1 - \sqrt { 17 } } { 2 } \right) \left( x - \dfrac { 1 + \sqrt { 17 } } { 2 } \right).
c. Déduire des questions précédentes les valeurs exactes des solutions de (\text{E}).
2. À l'aide de la calculatrice, déterminer un encadrement d'amplitude 10^{-2} des solutions \alpha et \beta.
3. a. Démontrer que, pour tout réel x , f ( x ) = ( x - 1 ) \left( x ^ { 2 } - x - 4 \right).
b. Démontrer que, pour tout réel x ,
x ^ { 2 } - x - 4 = \left( x - \dfrac { 1 - \sqrt { 17 } } { 2 } \right) \left( x - \dfrac { 1 + \sqrt { 17 } } { 2 } \right).
c. Déduire des questions précédentes les valeurs exactes des solutions de (\text{E}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8
Étudier le signe des fonctions définies sur \mathcal { D } par : 1. f ( x ) = 5 x ^ { 3 } avec \mathcal { D } = \mathbb { R }.
2. g ( x ) = - 5 ( x - 3 ) ( x + 2 ) avec \mathcal { D } = \mathbb { R }.
3. h ( x ) = \dfrac { 2 x - 3 } { 10 - 5 x } avec ] - \infty\:; 2 [ \cup ] 2\:; + \infty [.
4. \ell ( x ) = ( 5 - 2 x ) - ( 6 x + 2 ) avec \mathcal { D } = \mathbb { R }.
5. p ( x ) = - \sqrt { 2 x + 6 } avec \mathcal { D } = [ - 3\:; + \infty [.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9
1. f est la fonction définie sur \mathbb { R } par f ( x ) = x ^ { 2 } + 4 x - 5.
a. Démontrer que, pour tout x \in \mathbb { R }, f ( x ) = ( x + 2 ) ^ { 2 } - 9.
b. En déduire la forme factorisée de f .
2. g est la fonction définie sur \mathbb { R } par g(x) = 3(x - 1)^2 - 12 . Déterminer la forme développée puis la forme factorisée de g .
3. h est la fonction définie sur \mathbb { R } par h ( x ) = \dfrac { 1 } { 5 } ( x - 3 ) ^ { 2 } - 5. Déterminer la forme développée puis la forme factorisée de h .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10
f est la fonction définie sur \mathbb { R } par : f ( x ) = x ^ { 3 } + 2 x ^ { 2 } - 2. On note C_{f} sa représentation graphique dans un repère ( \mathrm { O } ; \mathrm { I } , \mathrm { J } ).
Le zoom est accessible dans la version Premium.
2. a. Conjecturer la position relative de C_{f} et d en fonction des valeurs de x .
b. Démontrer ces conjectures.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11
On considère les fonctions f et g définies sur \mathbb { R } par : f ( x ) = x ^ { 3 } - 2 x + 1 et g ( x ) = 4 x ^ { 2 } - 2 x + 1. On note C_f et C_g les représentations graphiques des fonctions f et g dans un repère du plan.
1. À l'aide d'une calculatrice, on obtient l'affichage
suivant.
Le zoom est accessible dans la version Premium.
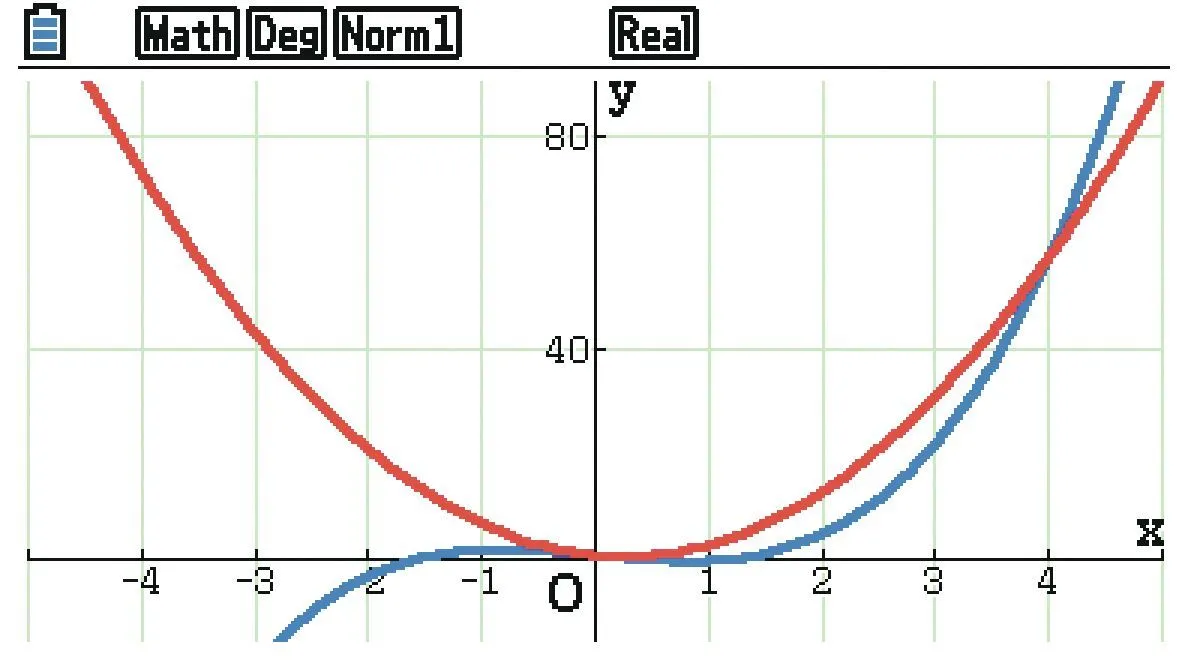
a. Conjecturer les coordonnées des points d'intersection
des courbes C_f et C_g.
b. Conjecturer la position relative des courbes C_f et C_g.
2. Démontrer les conjectures émises.
b. Conjecturer la position relative des courbes C_f et C_g.
2. Démontrer les conjectures émises.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12
f est la fonction définie sur \mathbb { R } par : f(x) = 2(x - 3)^2 - 18 . C_f est la représentation graphique de f dans un repère orthonormé du plan.
1. Déterminer la forme développée puis factorisée de f .
2. Étudier la position relative de C_f par rapport à l'axe des abscisses.
3. a. Calculer f(0) .
2. Étudier la position relative de C_f par rapport à l'axe des abscisses.
3. a. Calculer f(0) .
b. d est la droite passant par l'origine du repère et
le point de coordonnées \mathrm { A } \left( \dfrac { 1 } { 2 } \:; - 6 \right). Déterminer son équation réduite.
c. Étudier la position relative de C_f et d .
c. Étudier la position relative de C_f et d .
Aide
Pour étudier la position relative de deux courbes, il faut déterminer une inéquation à résoudre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13
f est la fonction définie sur \mathbb { R } par : f ( x ) = - 3 ( x - 1 ) ^ { 2 } + 27. C_f est la représentation graphique de f dans un repère orthonormé du plan.
1. Déterminer la forme développée puis factorisée de f .
2. À l'aide d'une calculatrice :
a. Étudier les variations de f sur \mathbb { R } puis dresser son tableau de variations.
2. À l'aide d'une calculatrice :
a. Étudier les variations de f sur \mathbb { R } puis dresser son tableau de variations.
Cliquez pour accéder à une zone de dessin
Cette fonctionnalité est accessible dans la version Premium.
b. Déterminer l'extremum de f sur \mathbb { R }.
3. Étudier le signe de f sur \mathbb { R }.
4. d est la droite d'équation y = 6x + 24 . Étudier la position relative de C_f et d .
3. Étudier le signe de f sur \mathbb { R }.
4. d est la droite d'équation y = 6x + 24 . Étudier la position relative de C_f et d .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14
f est une fonction définie sur \mathbb { R } ne s'annulant jamais sur \mathbb { R } et vérifiant, pour tous réels x et y , f(x + y) = f(x) \times f(y).
1. En posant y = 0 , justifier que f(0) = 1 .
2. Démontrer que, pour tout réel x , f(2x) = [f(x)]^2 .
2. Démontrer que, pour tout réel x , f(2x) = [f(x)]^2 .
3. Démontrer que, pour tout réel x, on a f ( - x ) = \dfrac { 1 } { f ( x ) }.
4. Démontrer que, pour tout réel x et y , on a f ( x - y ) = \dfrac { f ( x ) } { f ( y ) }.
4. Démontrer que, pour tout réel x et y , on a f ( x - y ) = \dfrac { f ( x ) } { f ( y ) }.
En classe de première, on démontre qu'il existe une fonction vérifiant ces conditions : la fonction exponentielle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
1. f est la fonction définie sur \mathbb { R } par : f(x) = x^3 + 4x^2 - 3x - 2 .
a. Vérifier que f(1) = 0 . On dit que 1 est une racine évidente de f , c'est-à-dire une solution simple de l'équation f(x) = 0 .
b. On considère trois réels a , b et c.
Justifier que ( x - 1 ) \left( a x ^ { 2 } + b x + c \right) = a x ^ { 3 } + ( b - a ) x ^ { 2 } + ( c - b ) x - c.
a. Vérifier que f(1) = 0 . On dit que 1 est une racine évidente de f , c'est-à-dire une solution simple de l'équation f(x) = 0 .
b. On considère trois réels a , b et c.
Justifier que ( x - 1 ) \left( a x ^ { 2 } + b x + c \right) = a x ^ { 3 } + ( b - a ) x ^ { 2 } + ( c - b ) x - c.
c. Pour déterminer a , b et c tels que f(x) = (x - 1)(ax^2 + bx + c) , on procède à une identification des coefficients en écrivant le système suivant :
\left\{ \begin{array} { c } { a = 1 } \\ { b - a = 4 } \\ { c - b = - 3 } \\ { - c = - 2 } \end{array} \right.
Résoudre ce système puis en déduire une forme factorisée de f .
2. g est la fonction définie sur \mathbb { R } par : g ( x ) = - x ^ { 3 } + 2 x ^ { 2 } + x - 2. En utilisant la méthode précédente, déterminer les réels a, b, c et d tels que g ( x ) = ( x - d ) \left( a x ^ { 2 } + b x + c \right).
\left\{ \begin{array} { c } { a = 1 } \\ { b - a = 4 } \\ { c - b = - 3 } \\ { - c = - 2 } \end{array} \right.
Résoudre ce système puis en déduire une forme factorisée de f .
2. g est la fonction définie sur \mathbb { R } par : g ( x ) = - x ^ { 3 } + 2 x ^ { 2 } + x - 2. En utilisant la méthode précédente, déterminer les réels a, b, c et d tels que g ( x ) = ( x - d ) \left( a x ^ { 2 } + b x + c \right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
f est une fonction définie sur ] 0\: ; + \infty [ telle que pour tous réels x \gt 0 et y \gt 0, f(x \times y) = f(x) + f(y).
1. En posant y = 1 , justifier que f(1) = 0 .
2. Démontrer que, pour tout réel x , f(x^2) = 2[f(x)] .
3. Démontrer que, pour tout réel x , f \left( \dfrac { 1 } { x } \right) = - f ( x ).
4. Démontrer que, pour tout réel x \gt 0 et y \gt 0, on a f \left( \dfrac { x } { y } \right) = f ( x ) - f ( y ).
2. Démontrer que, pour tout réel x , f(x^2) = 2[f(x)] .
3. Démontrer que, pour tout réel x , f \left( \dfrac { 1 } { x } \right) = - f ( x ).
4. Démontrer que, pour tout réel x \gt 0 et y \gt 0, on a f \left( \dfrac { x } { y } \right) = f ( x ) - f ( y ).
La fonction logarithme népérien dont voici la représentation graphique vérifie cette relation.
Le zoom est accessible dans la version Premium.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah