1. Résoudre une équation du second degré.
2. Résoudre une inéquation du second degré.
3. Factoriser et étudier le signe d'une fonction polynôme du second degré.
4. Déterminer la forme canonique d'une fonction polynôme du second degré à l'aide du discriminant.
5. Déterminer deux nombres réels connaissant leur somme et leur produit.
6. Choisir une forme adaptée d'une fonction polynôme du second degré dans le cadre de la résolution d'un problème.

1. Savoir développer et factoriser une expression littérale.
2. Connaître et savoir manipuler les identités remarquables.
3. Connaître les propriétés des racines carrées.
4. Savoir construire et analyser des tableaux de signes.

2

Factoriser avec ou sans identités remarquables

Factoriser les expressions suivantes définies pour tout réel x. 1. \mathrm{A}(x)=(3 x-1)^{2}-9

2. \mathrm{B}(x)=x^{2}+4 x+4-(5 x-3)(x+2)

3. \mathrm{C}(x)=4(1+2 x)^{2}-9 x^{2}

4. \mathrm{D}(x)=\left(x+\dfrac{3}{2}\right)^{2}-\left(\dfrac{1}{3} x+\dfrac{2}{3}\right)^{2}

1

Développer et factoriser

Les expressions suivantes sont définies pour tout réel x . 1. Développer et réduire.
a. \mathrm{A}(x)=12 x+3(x-2)-7(2 x-5)

b. \mathrm{B}(x)=(x+5)(3 x-2)+(x+5)(5 x+3)

c. \mathrm{C}(x)=5 x(x+2)-(3 x-1)(x+2)

2. Factoriser.
a. \mathrm{D}(x)=10 x^{4}-5 x^{2}

b. \mathrm{E}(x)=(3 x-1)(4 x+7)-(4 x+7)(5 x-2)

c. \mathrm{F}(x)=5 x(6-2 x)-(x-3)(x+7)

3

Résoudre des équations simples

1. Résoudre dans \R les équations suivantes.
a. 3 x+4=0

b. (2 x-1)(x+5)=0

c. x^{2}-4=0

d. 9 x^{2}-6 x+1=0

2. Résoudre dans \R les équations suivantes.
a. Démontrer que, pour tout x \in \R, (2 x-5)(3 x+1)=6 x^{2}-13 x-5.

b. En déduire les solutions réelles de 6 x^{2}-13 x-5=0.

4

Résoudre des inéquations simples

Résoudre dans \R les inéquations suivantes. 1. 3 x+4>0

2. (2 x-1)(x+5) \geqslant 0

3. x^{2}-4>0

4. 9 x^{2}-6 x+1\lt0

5. \dfrac{2 x-5}{3 x+1} \geqslant 0

7

Utiliser une représentation graphique

À l'aide de la calculatrice, on a représenté en rouge une fonction f et en bleu une fonction g, toutes les deux définies sur \R.
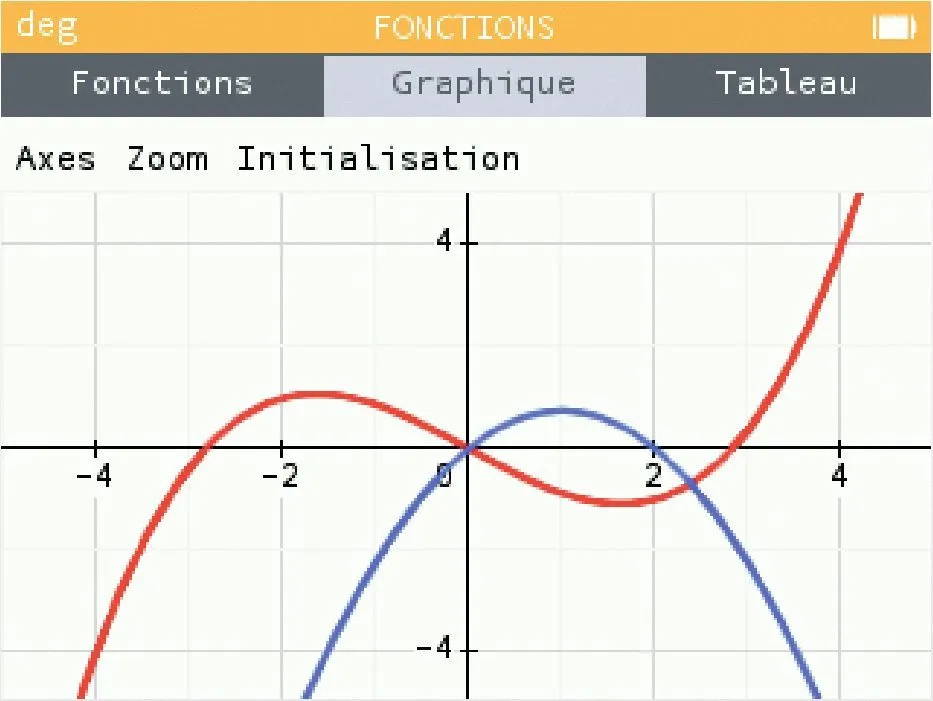
En utilisant cette représentation graphique, conjecturer le tableau de signes de la fonction f - g sur \R.

Au IX^e siècle, les mathématiciens arabes écrivaient les équations en toutes lettres. L'inconnue était appelée « la chose » et le carré de l'inconnue « le carré ».

8

Problème

Pour tout réel x , on pose :
\mathrm{A}(x)=16 x^{2}-25-3(4 x+5)(x-2) 1. Développer \text{A}(x).

2. Factoriser \text{A}(x).

3. Résoudre dans \R les équations et inéquations suivantes.
a. \mathrm{A}(x)=0

b. \mathrm{A}(x)-5=0

c. \mathrm{A}(x)-9 x=0

d. \mathrm{A}(x)>0

e. \mathrm{A}(x) \leqslant 0