Équation du second degré

40

[Calculer.]

1. \dfrac{1}{3} x^{2}-x-1=0

2. -x^{2}+\sqrt{3} x+3=0

3. \dfrac{(2 x-1)^{2}}{2}=3

4. -2 x^{2}+\dfrac{x}{4}=1

47

[Calculer.]
Donner le domaine de définition des fonctions suivantes.

1. f : x \mapsto \dfrac{1}{2 x^{2}+3 x-5}

2. g : x \mapsto \dfrac{7-x}{-x^{2}+x-3}

3. h : x \mapsto \dfrac{3}{4 x^{3}-x^{2}-3 x}

4. \ell : x \mapsto \dfrac{\sqrt{x}}{x^{2}+x-5}

48

[Calculer.]
On considère la parabole \mathcal{P} d'équation y=a x^{2}+b x+c où a, b et c sont trois réels tels que a \neq 0.

1. a. Déterminer le point d'intersection de \mathcal{P} avec l'axe des ordonnées.

b. On considère une droite d_{1} d'équation x = k où k est un réel quelconque.
Justifier que, pour toute valeur de k, la droite d_{1} coupe la parabole \mathcal{P} en un seul point. Déterminer alors les coordonnées de ce point.

2. a. Dans quels cas existe-t-il au moins un point d'intersection entre \mathcal{P} et l'axe des abscisses ? Justifier.

b. On considère une droite d_{2} d'équation y = k où k est un réel quelconque. On s'intéresse aux éventuels points d'intersection entre d_{2} et \mathcal{P}. Déterminer, en justifiant, tous les cas possibles. Pour chacun des cas, exprimer la condition respectée par k en fonction de \Delta et a.

49

[Raisonner.]
Noam a saisi l'expression de la fonction f sur sa calculatrice et a obtenu la courbe suivante.

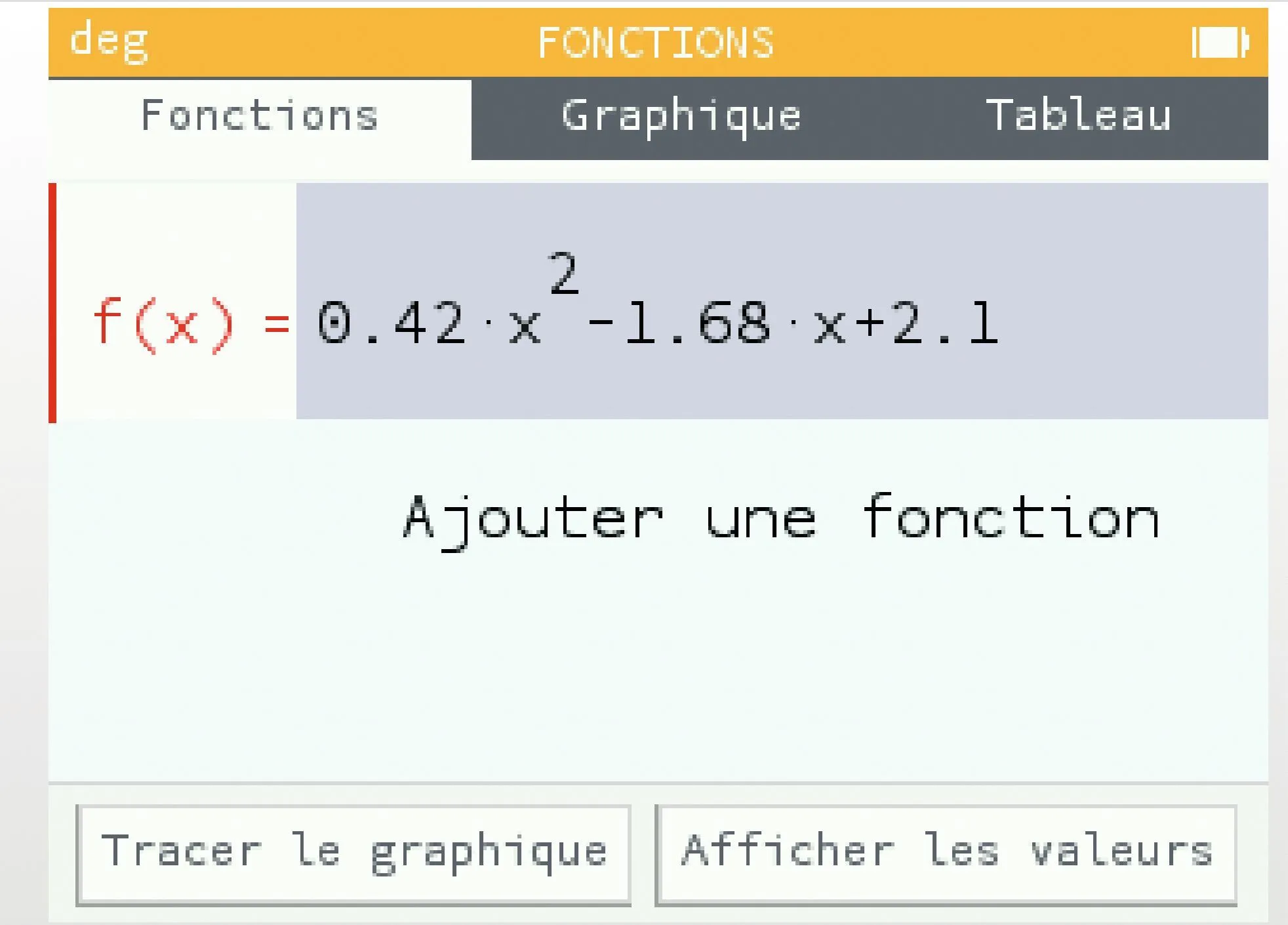
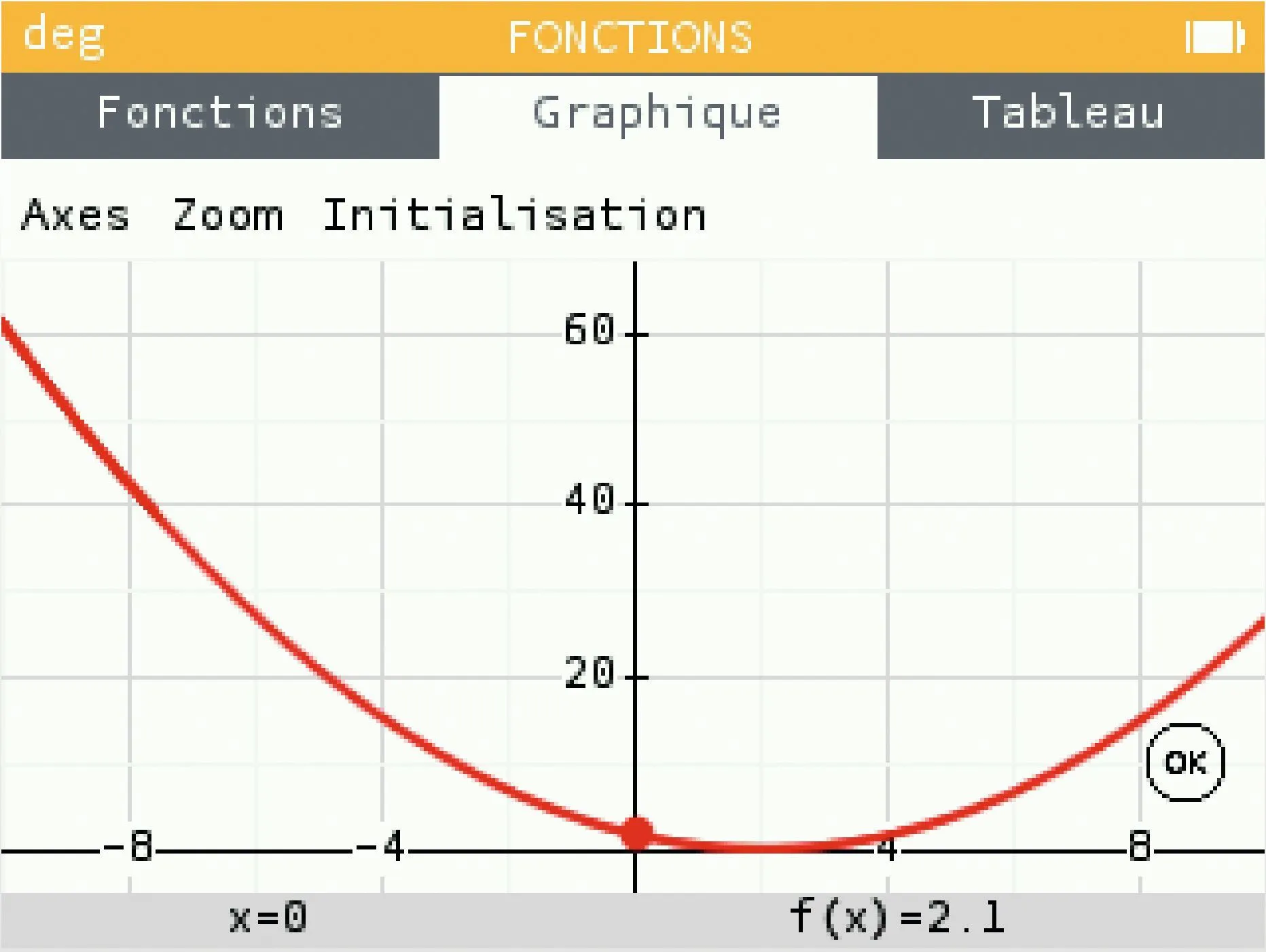
1. Conjecturer le nombre de solutions de l'équation f(x)=0 sur [-10 \: ; 10].

2. Vérifier cette conjecture en modifiant le zoom sur la calculatrice.

3. Démontrer cette conjecture.

50

Python

[Modéliser.]
On considère l'équation (\mathrm{E}) : a x^{2}+b x+c=0 où a, b et c sont des réels tels que a \neq 0.

1. Écrire un algorithme en langage naturel qui retourne le nombre de solutions de l'équation (\mathrm{E}).

2. Écrire en Python dans la console une fonction delta (a, b, c) qui retourne le discriminant de (\mathrm{E}).

3. En Python, à quoi sert l'instruction elif ?

4. Compléter les lignes 4 ; 5 et 8 du programme ci-dessous.

 def nombre_solutions(a, b, c):
    discriminant = delta(a, b, c)
    if discriminant < 0:
      return ...
    elif discriminant ...:
      return 1
    else:
      return ...
 

5. Écrire dans la console un autre programme qui donne les solutions lorsqu'elles existent.

51

[Chercher.]
Julie a saisi l'expression des fonctions f et g sur sa calculatrice et a obtenu les écrans suivants.

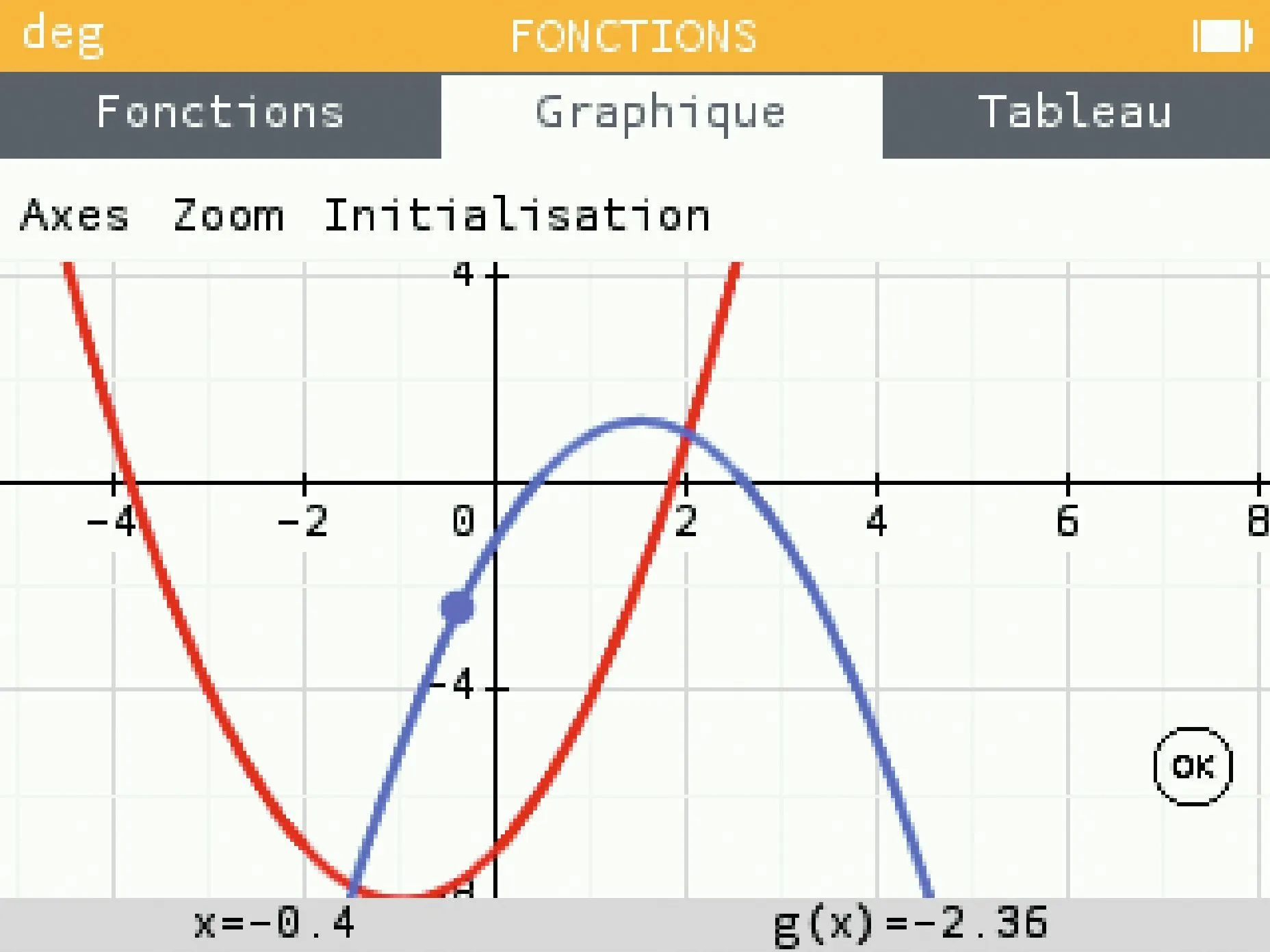
Déterminer l'ordonnée des deux points d'intersection des courbes représentatives des fonctions f et g.

55

[Chercher.]

Un architecte travaille sur le plan d'une maison. Le plan de l'étage est schématisé par la figure ci-dessous. \text{ABCD} et \text{BGFE} sont deux carrés.
Le rectangle \text{EFHC}, d'une largeur de 1,15 m, représente le balcon sur lequel donne la chambre principale.
On appelle x la longueur (en mètre) du côté du plus petit des deux carrés. L'étage doit avoir une surface de plancher de 80 m². Le balcon n'est pas pris en compte.

Déterminer la valeur de x.

56

[Chercher.]
On pourra éventuellement se servir de GeoGebra.
Soit \mathcal{H} la courbe d'équation y=\dfrac{1}{2 x+3} définie pour x \neq-\dfrac{3}{2} et \mathcal{D} la droite d'équation y=x-1.
Le but de cet exercice est de déterminer les coordonnées des points d'intersection de ces deux courbes.

1. Construire \mathcal{H} et \mathcal{D} à l'aide de la calculatrice ou de GeoGebra.

2. Déterminer graphiquement les valeurs approchées des coordonnées des points d'intersection des deux courbes.

3. Par le calcul, déterminer les coordonnées exactes de ces points d'intersection.

58

[Calculer.]
Équation bicarrée
Résoudre les équations suivantes.

1. 2 x^{4}-3 x^{2}+1=0

2. x^{4}+2 x^{2}-3=0

3. 3 x^{4}+5 x^{2}+2=0

4. 3 x^{4}-x^{2}+5=0

59

[Raisonner.]

Bac ES - Asie - 2015
Soit f la fonction définie sur [0 \: ; 1] par f(x)=2-2 x.
On a tracé ci-dessous la droite \mathrm{D}_{f}, représentation graphique de la fonction f dans un repère orthonormé (\mathrm{O} ; \mathrm{I}, \mathrm{J}) du plan.
Le point \text{C} a pour coordonnées (0 \: ; 2).
\Delta est la partie du plan intérieure au triangle \text{OIC}.
Soit a un nombre réel compris entre 0 et 1 . On note \text{A} le point de coordonnées (a \: ; 0) et \text{B} le point de \mathrm{D}_{f} de coordonnées (a \: ; f(a)).
Le but de cet exercice est de trouver la valeur de a telle que le segment [\text{AB}] partage \Delta en deux parties de même aire.